
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Степенные ряды. Ряд , члены которого функции от x, называется функциональным.
Ряд 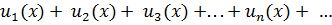 , члены которого функции от x, называется функциональным.
, члены которого функции от x, называется функциональным.
Совокупность значений х, при которых функции 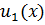 ,
,  ,
,  ,…,
,…,  определены и ряд
определены и ряд  сходится, называют областью сходимости функционального ряда.
сходится, называют областью сходимости функционального ряда.
Функциональный ряд вида  , где
, где  ,
,  ,
,  , …,
, …,  ,
,  - действительные числа, называется степенным.
- действительные числа, называется степенным.
При  степенной ряд имеет вид:
степенной ряд имеет вид: 
Разложение функции в ряд Тейлора. Ряд Маклорена
Формула Тейлора для многочлена
Пусть функция f(x) есть многочлен n –ной степени, т.е.
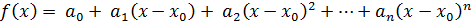
Коэффициенты a0, a1, a2, . . . an находим из соотношения:

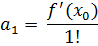


. . . . . . . . .

Тогда, формула Тейлора будет иметь вид:


При  получим формулу Маклорена для многочленов:
получим формулу Маклорена для многочленов:

Пример. Составить ряд Тейлора для функции  в окрестности точки х0 = 3.
в окрестности точки х0 = 3.
Решение:
1) 
2) 

3) 

4) 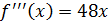

5) 

6) 

Тогда ряд Тейлора имеет вид:



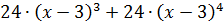
Дата добавления: 2015-02-09; просмотров: 96; Мы поможем в написании вашей работы!; Нарушение авторских прав |