Классический метод анализа переходных процессов.

Предварительные соглашения. При анализе переходных процессов в электрических цепях считается, что:

1. Рубильники включаются и размыкаются мгновенно, без возникновения электрической дуги;

2. Время переходного процесса, теоретически бесконечно длительное, (переходный режим асимптотически приближается к новому установившемуся режиму), ограничивают условным пределом – длительностью переходного процесса;

3. Установившийся режим после коммутации рас-считывают при теоретическом условии t→∞, т.е. когда после коммутации прошло бесконечно большое время.

Установившийся режим до коммутации рассчитывают обычно в предположении, что к моменту коммутации в цепи закончился предыдущий переходный процесс. Хотя иногда приходится анализировать переходные процессы, возникающие в цепи, когда предыдущий переходный процесс, вызванный прежними коммутациями, еще не закончился. Но это не изменяет теоретическую постановку задачи.

Содержание классического метода. Анализ переходных процессов классическим методом производят путем решения дифференциальных уравнений, составленных для исследуемой электрической цепи на основе законов Кирхгофа или метода контурных токов.

Пусть в некоторой цепи (рис. 2.41, а) внезапно изменяется сопротивление. До коммутации в цепи существовали сопротивления R₁ и R, после коммутации остается только R. Требуется определить переходный ток i.

Электрическое состояние схемы после коммутации описывается интегро-дифференциальным уравнением, записанным на основании II закона Кирхгофа для мгновенных значений токов и напряжений:

а b c

Рис. 2.41

Если это уравнение продифференцировать по времени получим линейное дифференциальное уравнение второго порядка, у которого в качестве постоянных коэффициентов выступают параметры цепи или их комбинации:

(2.13)

Из математики известно, что полное решение линейного дифференциального уравнения с постоянными коэф-фициентами находят в виде суммы частного решения неоднородного и общего решения соответствующего однородного уравнения.

Поскольку в правой части дифференциальных уравнений, описывающих электрическое состояние цепей, обычно находится напряжение (или ток) источника (внешняя вынуждающая сила), то частное решение находят из анализа установившегося режима после коммутации. Отсюда этот режим называют вынужденным и соответственно токи или напряжения, найденные в данном режиме, называют вынужденными. Расчет вынужденного режима, когда внешние источники вырабатывают постоянную э.д.с. (ток), не представляет трудностей и может быть осуществлен любым известным методом.

Однородное дифференциальное уравнение получают из выражения (4.12) путем "освобождения" его от правой части. Физически это означает, что исследуемая цепь "освобождается" от внешней вынуждающей силы. Токи или напряжения, найденные при решении однородного дифференциального уравнения, называются свободными. Свободные токи и напряжения являются результатом действия внутренних источников схемы: э.д.с. самоиндукции, возникающих в катушках, и напряжений на конденсаторах, когда и те, и другие не уравновешены внешними источниками.

Схематически анализ переходного процесса может быть представлен как результат наложения двух режимов: вынужденного и свободного. Схема на рис. 4.5, b должна быть рассчитана в установившемся (вынужденном) режиме, а схема на рис. 4.5, c − в режиме, когда цепь освобождена от внешних источников. Действительный (переходный) ток в соответствии с принципом суперпозиции равен сумме установившегося (вынужденного) и свободного токов:

i = i_вын + i_св.

Замечание 1. Физически существует только переходные токи и напряжения, а разложение их на свободные и вынужденные составляющие является математическим приемом, позволяющим упростить расчет переходных процессов в линейных цепях.

Замечание 2. Напомним, что принцип суперпозиции применим лишь к линейным цепям.

Существуют различные методы решения однородного дифференциального уравнения, полученного из выражения (2.13):

(2.14)

Классический метод анализа переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений. Решение находят в виде суммы экспонент:

i_св = A₁e^p₁^t + A₂·e^p₂^t,

где число слагаемых равно порядку дифференциального уравнения.

После подстановки экспонент A_k·e^p_k^t в исходное уравнение (2.14) и дифференцирования можно получить характеристическое уравнение, из которого определяют корни p₁, p₂. Если встречаются кратные корни (например, p₁ = p₂ = P), решение имеет вид

A₁·e^Pt+ A₂·e^Pt.

Постоянные интегрирования A₁, A₂ находят из начальных условий, которые определяют с помощью законов коммутации. Различают независимые и зависимые (послекоммутационные) начальные условия. К первым относят значения токов через индуктивности и значения напряжений на емкостях, известные из докоммутационного режима работы цепи.

Значения остальных токов и напряжений при t = 0 в после коммутационной схеме, определяемые по незави-симым начальным значениям из законов Кирхгофа для схемы после коммутации, называют зависимыми началь-ными значениями.

Алгоритм расчета переходного процесса классическим методом.Для анализа переходного процесса предварительно следует привести схему к минимальному числу накопителей энергии, исключив параллельные и последовательные соединения однотипных реактивных элементов (индуктивностей или емкостей). Система интегро-дифференциальных уравнений, составленных в соответствии с законами Кирхгофа или методом контурных токов, может быть сведена путем подстановки к одному дифференциальному уравнению, которое используется для составления характеристического уравнения.

Порядок дифференциального, следовательно, и характеристического уравнения зависит от числа реактивных элементов приведенной схемы. Главная трудность в решения задачи классическим методом для уравнений высоких порядков состоит в отыскании корней характеристического уравнения и постоянных интегрирования.

План анализа:

1. Рассчитать вынужденный (установившийся) режим при t → ∞. Определить вынужденные токи и напряжения.

2. Рассчитать режим до коммутации. Определить токи в ветвях с индуктивностью и напряжения на конденсаторах. Значения этих величин в момент коммутации является независимыми начальными условиями.

3. Составить дифференциальные уравнения для свободного процесса (Е = 0) в схеме после коммутации по законам Кирхгофа или по методу контурных токов. Алгебраизировать данные уравнения, получить характеристическое уравнение и найти его корни.

4. Записать общие выражения для искомых напряжений и токов в соответствии с видом корней характеристи-ческого уравнения.

5. Переписать величины, полученные в п. 4, и производные от них при t = 0.

6. Определить необходимые зависимые начальные условия, используя независимые начальные условия.

7. Подставив начальные условия в уравнения п. 5, найти постоянные интегрирования.

8. Записать законы изменения искомых токов и напряжений.

В данном разделе предполагается не только практическое знакомство с классическим методом расчета переходных процессов, но и с особенностями самих процессов в рассматриваемых задачах.

Переходные процессы в цепях первого порядка. Рассмотрим применение классического метода к расчету переходных процессов в цепях первого порядка. Это цепи, содержащие только однотипные реактивные элементы (емкости или индуктивности), процессы, в которых описываются дифференциальными уравнениями первого порядка

Примером цепей первого порядка являются простейшие RL-(последовательное соединение резистора и катушки индуктивности) и RC- (последовательное соединение резистора и конденсатора) цепи. Переходные процессы в них обычно рассматриваются в режимах короткого замыкания и подключения их на постоянное напряжение.

Переходные процессы в RC-цепях.При расчете переходных процессов в RC-цепях в качестве независимой переменной выбирают u_c.Затем составляют дифференциальное уравнение для заданной RC-цепи, решение которого с учетом начальных условий для и_с(0)и определяет закон изменения напряжения на емкости.

Подключение реального конденсатора к источнику постоянного напряжения (заряд конденсатора).Рассмотрим вначале RС-цепь при нулевых начальных условиях (рис. 2.42), которая подключается в момент t = 0 к источнику постоянного напряжения u(t) = U. Переходный процесс в данной цепи описывается дифференциальным уравнением

,

решение которого ищем в форме суммы общего и частного решений, определяющих свободную и вынужденную составляющие.

Рис. 2.42

При подключении RC-цепи к источнику постоянного тока (при U_c(0) = 0) на обкладках конденсатора начинается накопление зарядов и напряжение постепенно увеличивается до U.

1. Составим систему уравнений электрического состояния. Так как схема одноконтурная, то можно написать только одно уравнение по второму закону Кирхгофа:

Ri + u_С = U.

В этом уравнении во время переходного процесса происходит изменение двух величин: тока i и напряжения на емкостном элементе u_С . Напряжение u_С подчиняется второму закону коммутации, поэтому рационально выразить ток по закону Ома

Тогда уравнение примет вид

.

2. Ищем решение этого уравнения как сумму двух

слагаемых:

u_С = u_Свын + u_Ссв.

3. Найдем u_Свын .

Теоретически переходной процесс длится бесконечно долго, поэтому вынужденный режим рассмотрим как новый установившийся режим при t = ∞. Конденсатор постоянный ток не пропускает (i_вын = 0), Ri_вын = 0. Отсюда

u_Свын =U.

4. Вычислим u_Ссв. Из математики известно, что свободные составляющие меняются по экспоненциальному закону:

u_Ссв = А е^pt.

5. Определим показатель степени р, который является корнем характеристического уравнения.

Запишем уравнение электрического состояния для свободной составляющей:

Производной экспоненты является сама экспонента. Так как функция сложная, дифференцируем еще и показатель степени.

В итоге производная равна

.

После подстановки в уравнение электрического состояния получаем

RCpAe^pt + Ae^pt = 0.

Сократим на Ae^pt:

RCp +1 = 0.

Сравнив уравнение электрического состояния с характеристическим, делаем вывод: для получения характеристического уравнения в уравнении электрического состояния правую часть нужно приравнять к нулю, переменную величину заменить единицей, ее производную – р, вторую производную – р² и т. д.

Решение характеристического уравнения позволяет определить

.

Величину

обозначают τ и называют постоянной времени.

Показатель степени равен

.

Так как [R]= Ом, [C]= Ф = с/Ом , то [τ]= с .

Постоянная времени τ – это время, в течение которого свободные составляющие уменьшаются в е раз по сравнению с начальным значением.(см. рис. 2.43).

Рис. 2.43

Время t₂ − t₁ = τ , если

Постоянной времени можно дать геометрическую

интерпретацию:

τ – это величина подкасательной к любой точке экспоненты (рис. 2.44).

Рис. 2.44.

Поэтому можно определить постоянную времени по известному графику изменения свободной составляющей и неизвестных параметрах схемы.

6. Определим постоянную интегрирования А.

Постоянные интегрирования определяют из начальных условий с использованием законов коммутации.

Уравнение, по которому проводим решение, справедливо для любого момента времени, следовательно, и для начального:

u_С(0₊) = u_Свын(0₊) + u_Ссв(0₊).

По второму закону коммутации

u_С(0₊) = u_С(0₋) .

До коммутации схема не была подключена к источнику энергии, поэтому

u_С(0₋) = 0.

Вынужденная составляющая в данном примере является постоянной величиной, значит

u_Свын (0₊) = U.

Свободная составляющая

u_Ссв = Ае^рt

при t = 0₊ равна А.

После подстановки получим

0 = U + A.

Отсюда

A = −U .

Тогда закон изменения напряжения

.

Закон изменения тока можно получить как из уравнения по второму закону Кирхгофа, так и из закона Ома.

Из уравнения по второму закону Кирхгофа

либо

Проиллюстрируем полученные уравнения графиками.

График напряжения u_С (рис. 2.45) получаем суммированием графиков u_Свын и u_Ссв .

Составляющая u_Свын = U = const .

Свободная составляющая изменяется по закону экспоненты и стремится к нулю. В начальный момент

u_Ссв (0₊) = −U .

Рис. 2.46

График подтверждает, что напряжение на конденсаторе меняется плавно, что вынужденный режим – это новый установившийся режим после переходного процесса.

График изменения тока представлен на рис. 2.47.

Рис. 2.47.

При t = 0_– тока не было, при t = 0₊ ток

,

далее он стремится к нулю по закону экспоненты.

Графики будут меняться при изменении параметров схемы R и С. Величина напряжения от них не зависит. Величина тока обратно пропорциональна сопротивлению R и не зависит от емкости С. Длительность переходного процесса прямо пропорциональна значениям R и С.

Разряд конденсатора на резистор. Рассмотрим переходный процесс при коротком замыкании в цепи с конденсатором и резистором (рис. 2.48), если предварительно конденсатор был заряжен до напряжения

u_C(0₊) = U₀ = Е.

Рис. 2.48.

Установившийся ток через конденсатор и установившееся напряжение на конденсаторе равны нулю. Для построения характеристического уравнения запишем по второму закону Кирхгофа уравнение для вновь образованного контура

R i + u_C = 0.

При расчете переходных процессов в цепях с конденсатором часто удобнее отыскать сначала не ток, а напряжение на конденсаторе u_C, а затем, учитывая, что

,

найти ток через конденсатор. Поэтому запишем уравнение по второму закону Кирхгофа в виде:

.

Характеристическое уравнение имеет вид:

RCp + 1 = 0.

Общее решение для свободной составляющей напряжения:

u_Cсв = A e^pt = A e^-t/τ,

где: А = Е₁ – постоянная интегрирования;

p = − 1/(RC) – корень характеристического уравнения;

τ = RC – постоянная времени цепи.

С учетом нулевого значения установившегося напряжения получим напряжение на конденсаторе:

u_C = Е₁ e^-t/τ.

Переходный ток в цепи

.

Кривые изменения напряжения на конденсаторе и тока в цепи во времени имеют вид экспонент (рис. 2.49).

Рис. 2.49

Теоретически переходный процесс длится бесконечно

долго. Практически переходный процесс заканчивается через (3–5) τ.

Длительность переходного процесса, зависящая от параметров, может быть различной.

Если в схеме замещения R = 100 Ом, С = 100 мкФ, то при замыкании ключа конденсатор заряжается с постоянной времени τ_зар = 0,01 с. При размыкании ключа конденсатор будет разряжаться с τ_раз ≈ 28 часов, т. е. конденсатор будет сохранять напряжение на своих обкладках несколько суток и представлять собой опасность. Поэтому после окончания работы с конденсатором нужно использовать разрядное устройство.

С энергетической точки зрения переходный процесс характеризуется переходом энергии электрического поля конденсатора в тепловую энергию в резисторе. Следует отметить; что сопротивление резистора влияет не на количество выделенной теплоты, а на начальное значение тока и длительность разряда. В самом деле

.

Переходные процессы в электрических RL-цепях.Рассмотрим следующие варианты RL-цепей и способов их коммутации:

− последовательная RL-цепь в режиме подключения к источнику постоянного напряжения;

− последовательная RL-цепь в режиме короткого замыкания;

− последовательная RL-цепь в режиме размыкания.

Включение цепи с резистором и катушкой на постоянное напряжение (рис 2. 50). В начальный момент времени i = 0, энергия магнитного поля катушки W_м = 0. После подключения цепи к источнику постоянного напряжения U в установившемся режиме в цепи протекает ток I > 0 и W_м = LI²/2 > 0.

Рис. 2. 50.

Дифференциальное уравнение, описывающее переходной процесс в цепи имеет вид

.(*)

Характеристическое уравнение данного дифференциального уравнения есть

, p = − R/L.

Переходный ток в цепи представим в виде

i = i_вын + i_св.

1. До коммутации тока в катушке не было, следовательно,

i_L(0_-) = 0.

2. Установившаяся составляющая тока после коммутации

I_вын = U/R.

3. Свободная составляющая тока для цепи, описываемой дифференциальным уравнением первого порядка (*)

i_св = A e^-t/τ = A e^pt .

4. По начальным условиям определим постоянную интегрирования А и свободную составляющую тока:

i(0) = i_вын(0) + i_св(0) = i_вын(0₊) + i_св(0_-);

или

0 = U/R + A; A = −U/R; i_св = −U/R·e^-t/τ.

Переходный ток получается в виде

i = U/R (1 − e^-t/τ).

Напряжение на катушке

.

Кривые изменения токов i, i_вын, i_св и напряжения на катушке u_L показаны на рис. 2.51.

Рис. 2.51

При включении рассматриваемого контура под постоянное напряжение ток в нем нарастает от нуля до установившегося значения.

Скорость нарастания тока изменяется по экспоненте с отрицательным показателем. В момент t = 0 эта скорость максимальна и равна U/L [А/с], со временем она падает практически до нуля, процесс выходит на установившийся режим.

В первый после коммутации момент t = 0₊ ток в цепи еще равен нулю, и напряжение на катушке максимально u_L = U, далее оно экспоненциально снижается до нуля.

Последовательная RL-цепь в режиме короткого замыкания.Исследуем электромагнитные процессы в цепи, изображенной на рис. 2.52, происходящие после замыкания ключа.

Рассчитаем установившийся режим в цепи до коммутации (до замыкания ключа) и определим из него

Рис. 2.52

независимое начальное условие – ток в катушке в момент t = 0_-, непосредственно предшествующий коммутации

i(0_-) = i(0₊) = E/(R₀ + R).

Найдем установившийся ток i после коммутации. Так как во вновь образованном контуре из катушки L и резистора R нет источника, то

I_вын = 0.

Для определения свободной составляющей тока запишем по второму закону Кирхгофа уравнение электрического состояния цепи после коммутации:

.

Характеристическое уравнение имеет вид:

pL + R = 0,

где p = - R/L, c^-1 – корень характеристического уравнения.

Общее решение уравнения для свободной составляющей:

i_св = Ae^pt,

где А – постоянная интегрирования.

Записав общий вид переходного тока катушки

i = i_вын + i_св = A e^pt,

приравниваем его значение i(0₊) = A в точке t = 0₊ к значению i(0_-), найденному в п. 1. Получаем искомую константу

A = E/(R₀ + R) = I₀.

Переходный ток i = i_вын + i_св при этом равен

,

где τ = L/R – постоянная времени цепи.

График изменения переходного тока показан на рис. 2.53.

Рис. 2.53.

Определим э.д.с. самоиндукции катушки

, t ≥ 0.

В момент коммутации эта ЭДС равна напряжению на сопротивлении R, а в дальнейшем уменьшается по экспоненциальному закону. На основании изложенного можно сделать следующие выводы.

1. При коротком замыкании в рассматриваемой цепи ток в ней изменяется по экспоненциальному закону, уменьшаясь от начального значения до нуля.

2. Скорость изменения тока определяется постоянной времени цепи, которая равна индуктивности катушки, деленной на активное сопротивление цепи.

3. Практически можно считать, что переходный процесс заканчивается при t ≈ (3…5)τ, когда первоначальное значение тока уменьшается по модулю на порядок.

4. Напряжение на катушке в начальный момент времени равно напряжению на активном сопротивлении:

u_L(0₊) = I₀R.

5. С энергетической точки зрения рассматриваемый переходный процесс характеризуется расходом энергии магнитного поля катушки на тепловые потери в резисторе. Следует отметить, что сопротивление резистора влияет не на количество выделенной теплоты W, а на начальное значение напряжения катушки и длительность процесса. В самом деле

.

Последовательная RL-цепь в режиме размыкания. При размыкании электрической цепи с индуктивностью (рис. 2. 54) между контактами возникает дуга, а на отдельных участках цепи могут возникать перенапряжения.

Рис. 2. 54

Установившийся (т.е. до размыкания цепи) ток в ветви с индуктивностью равен

.

Уравнение напряжений для цепи (рисунок 2.54) после коммутации

.

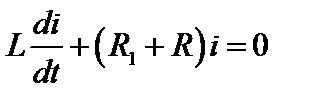Характеристическое уравнение

, .

Решением однородного уравнения является показательная функция

.(**)

Постоянную интегрирования находим из начальных условий. При t = 0

.

Подставляя выражение для тока в (**), получим

.

Тогда переходной ток

При изменении тока возникает ЭДС самоиндукции

или

.

Ток в цепи после коммутации (после размыкания) поддерживается за счет ЭДС самоиндукции

.

Значение ЭДС самоиндукции в первый момент после размыкания цепи (при t = 0)

.

Оно больше ЭДС источника E во столько раз, во сколько увеличилось сопротивление цепи, то есть в (R₁+ R)/R раз. Это явление называется перенапряжением.

Графики изменения тока и ЭДС самоиндукции представлены на рисунке 2.55.

ЭДС самоиндукции в начальный момент времени делает скачок. Ток же в индуктивности согласно первому закону коммутации не может изменяться скачком. Он изменяется постепенно от начального значения I₀.

Рис. 2.55

При отсутствии ветви с R₁ перенапряжение должно быть равно ∞, но на самом деле происходит пробой промежутка между контактами выключателя и в цепь включается сопротивление дуги. Часто вместо R₁ включают диод.

Переходные процессы в цепях второго порядка. Ранее рассматривались переходные процессы в RL- и RС-цепях, которые относятся к цепям первого порядка, так как описываются дифференциальными уравнениями первого порядка (6.11), (6.23). При наличии в цепи двух независимых накопителей энергии переходные процессы в них описываются уравнением второго порядка.

Простейшим примером такой цепи является последовательный колебательный контур (рис. 2.56).

Рис. 2.56.

Для этого контура можно по аналогии с RL- и RC-цепью составить дифференциальное уравнение второго порядка, выбрав в качестве независимой переменной напряжение на емкости

Учитывая, что

окончательно получаем

(2.15)

Решение дифференциального уравнения (2.15) ищется в виде суммы свободной и вынужденной составляющих:

Вид зависит от приложенного напряжения, а определится решением однородного дифференциального уравнения второго порядка

(2.16)

Решение дифференциального уравнения (2.16) зависит от вида корней характеристического уравнения

(2.17)

Корни уравнения (2.17) определяются только параметрами цепи независимо от выбранной переменной:

.

Величина называется коэффициентом затухания контура, а − резонансной частотой контура. Тогда уравнение (6.41) можно представить в виде

Характер переходного процесса существенным образом зависит от вида корней p₁, p₂, которые могут быть:

1) вещественными и различными (при R > 2ρ);

2) комплексно-сопряженными (при R < 2ρ);

3) вещественными и равными (при R = 2 ρ).

Здесь — характеристическое сопротивление контура (см. формулу (4.22)).

Апериодический разряд конденсатора на катушку и резистор.Рассмотрим процесс разряда конденсатора на резистор R и катушку L. Если параметры контура из резистора, катушки и конденсатора удовлетворяют условию , т.е. или , т.е. то корни характеристического уравнения контура вещественные, различные, т.е. р₁ ≠ р₂, и отрицательные. В этом случае напряжение на конденсаторе описывается уравнением

u_C = u_Cсв = A₁·e^p₁^t + A₂·e^p₂^t,

где А₁ и А₂ – постоянные интегрирования, определяемые из начальных, условий.

Свободный ток равен

.

Установившиеся составляющие напряжения на конденсаторе и тока равны нулю. Поэтому их переходные значения равны свободным составляющим:

u_C = u_Cсв; i = i_св.

Определим из начальных условий постоянные интегрирования А₁ и А₂. При t = 0, u_C(0) = U₀ и i(0) = 0. Подставив их в выражения для переходных напряжений и токов при t = 0 имеем

U₀ = A₁ + A₂;

0 = A₁ p₁ + A₂ p₂.

Отсюда

A₁ = U₀ p₂ /(p₂ - p₁);

A₂ = -U₀ p₁ /(p₂ - p₁);

С учетом начальных условий запишем

;

.

Произведение корней по теореме Виета: p₁ p₂ = 1 / (LC), следовательно, ток

.

Напряжение на катушке

.

Графики зависимости тока и напряжения от времени, показанные на рис. 2.57 позволяют говорить об апериодическом разряде конденсатора.

Рис. 2.57.

Апериодическим называется такой разряд, при котором конденсатор все время разряжается, т.е. функция u_C(t) - убывающая, а ток i не меняет своего направления, в нашем случае он отрицателен. Сделаем некоторые выводы.

1. Апериодический разряд конденсатора в цепи R, L, С возникает при вещественных, отрицательных и неравных корнях характеристического уравнения.

2. При апериодическом разряде напряжение на конденсаторе уменьшается от начального значения до нуля, а ток сначала возрастает по модулю, затем уменьшается, проходя через максимальное значение.

3. Напряжение на катушке уменьшается от начального значения, проходит через нулевое значение, изменяя знак и, достигнув наибольшего значения, уменьшается до нуля.

Предельный апериодический разряд конденсатора на катушку и резистор.При соотношении параметров контура из конденсатора, катушки и резистора

,

где R_КР − критическое сопротивление резистора R, корни характеристического уравнения контура вещественные, равные и отрицательные:

p₁ = p₂ = p = −R/(2L).

Переходный процесс получается апериодическим, но граничным с колебательным процессом. Переходный ток и переходное напряжение в этом случае имеют вид:

u_C = (A₁ + A₂ t) e^pt;

.

При начальных условиях u_C(0) = U₀; i(0) = 0 находим: А₁ = U₀; A₂ = −pU₀. С учетом найденных постоянных интегрирования получаем решения:

u_C = U₀ (1 - pt)e^pt;
;
.

Зависимости i, u_C, u_L такие же, как для апериодического

разряда.

Периодический (колебательный) разряд конденсатора на цепь с резистором и катушкой.При соотношении параметров контура из конденсатора, катушки и резистора , где R_КР – критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные:

p_1,2 = -α ± jω₀,

где α = R/(2L) – коэффициент затухания свободной составляющей;

– угловая частота собственных колебаний контура;

Т₀ – период собственных колебаний.

Поскольку , то можно ввести обозначения

,

,

.

Свободная составляющая переходного напряжения при комплексно-сопряженных корнях

u_Cсв = A e^-αt sin(ω₀t + ψ),

Для свободной составляющей тока имеем

i_св = C A e^-αt (-α sin(ω₀t + ψ) + ω₀ cos(ω₀t + ψ)).

С учетом начальных условий при t = 0, u_C = U₀ , i = 0 из последних двух уравнений находим константы интегрирования:

U₀ = A sin ψ; 0 = C A (-α sin ψ + ω₀ cos ψ).

и далее

.

Запишем переходные напряжения и ток:

u_C = U_Cm e^-αt sin(ω₀t + ψ);

i = -I_m e^-αt sin(ω₀t + π);

u_L= U_Lm e^-αt sin(ω₀t - ψ),

где ;

Зависимости переходных напряжений и токов u_C, i показаны на рис. 2.56.

Рис. 2.56.

Они представляют собой затухающие синусоиды. Скорость затухания колебаний оценивают декрементом колебаний. Декремент колебания − это постоянная, зависящая от параметров R, L, С и равная отношению амплитуд переходных параметров, отстающих друг от друга на период колебания Т₀, например:

.

Часто пользуются логарифмическим декрементом колебания:

.

В предельном случае чисто консервативной системы (R = 0) Δ = 1 колебания в параллельно соединенных конденсаторе и катушке носят незатухающий характер. Период этих колебаний дается формулой Томпсона

,

а частота незатухающих колебаний .