
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Отыскание максимума линейной функции
В качестве первого примера рассмотрим задачу об использовании ресурсов, сформулированную в разд. 1.2 и уже решенную геометрически в задаче 2.1.
3.1. Решить симплексным методом задачу:
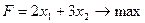
при ограничениях
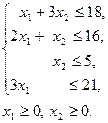 (3.1)
(3.1)
Решение. С помощью дополнительных неотрицательных переменных перейдем к системе уравнений. В данном случае все дополнительные переменные вводятся со знаком "плюс", так как все неравенства имеют вид "<".
Получим систему ограничений в виде:
 (3.2)
(3.2)
Для нахождения первоначального базисного решения разобьем переменные на две группы - основные и неосновные. Так как определитель, составленный из коэффициентов при дополнительных переменных x3, х4, х5, х6, отличен от нуля, то (см. разд. 2.1) эти переменные можно взять в качестве основных на первом шаге решения задачи. При выборе основных переменных на первом шаге не обязательно составлять определитель из их коэффициентов и проверять, равен ли он нулю. Достаточно воспользоваться следующим правилом:
в качестве основных переменных на первом шаге следует выбрать (если возможно) такие т переменных, каждая из которых входит только в одно из т уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.
Дополнительные переменные удовлетворяют этому правилу. Если выбранные по этому правилу переменные имеют те же знаки, что и соответствующие им свободные члены в правых частях уравнений, то полученное таким образом базисное решение будет допустимым. В данном случае так и получилось.
I шаг. Основные переменные 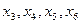 .
.
неосновные переменные 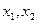 .
.

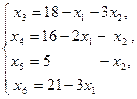 (3.3)
(3.3)
Положив неосновные переменные равными нулю, т.е. 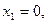
 , получим базисное решение
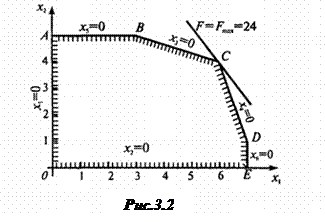
, получим базисное решение  = (0; 0; 18; 16; 5; 21), которое является допустимым и соответствует вершине О (0;0) многогранника OABCDE на рис. 3.2. Поскольку это решение допустимое, нельзя отбросить возможность того, что оно оптимально.
= (0; 0; 18; 16; 5; 21), которое является допустимым и соответствует вершине О (0;0) многогранника OABCDE на рис. 3.2. Поскольку это решение допустимое, нельзя отбросить возможность того, что оно оптимально.
Выразим линейную функцию через неосновные переменные:  . При решении
. При решении  значение функции равно
значение функции равно  . Легко понять, что функцию F можно увеличить за счет увеличения любой из неосновных переменных, входящих в выражение для F с положительным коэффициентом. Это можно осуществить, перейдя к такому новому допустимому базисному решению, в котором эта переменная будет неосновной, т.е. принимать не нулевое, а положительное значение (если новое решение будет вырождено, то функция цели сохранит свое значение). При таком переходе одна из основных переменных перейдет в неосновные, а геометрически произойдет переход к соседней вершине многоугольника, где значение линейной функции "лучше" (по крайней мере "не хуже"). В данном примере для увеличения F можно переводить в основные либо
. Легко понять, что функцию F можно увеличить за счет увеличения любой из неосновных переменных, входящих в выражение для F с положительным коэффициентом. Это можно осуществить, перейдя к такому новому допустимому базисному решению, в котором эта переменная будет неосновной, т.е. принимать не нулевое, а положительное значение (если новое решение будет вырождено, то функция цели сохранит свое значение). При таком переходе одна из основных переменных перейдет в неосновные, а геометрически произойдет переход к соседней вершине многоугольника, где значение линейной функции "лучше" (по крайней мере "не хуже"). В данном примере для увеличения F можно переводить в основные либо  , либо
, либо 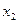 , так как обе эти переменные входят в выражение для F со знаком "плюс". Для определенности в такой ситуации будем выбирать переменную, имеющую больший коэффициент, т.е. в данном случае
, так как обе эти переменные входят в выражение для F со знаком "плюс". Для определенности в такой ситуации будем выбирать переменную, имеющую больший коэффициент, т.е. в данном случае 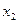 (такое правило выбора не всегда дает наименее трудоемкое решение, иногда имеет смысл провести предварительные специальные оценки).
(такое правило выбора не всегда дает наименее трудоемкое решение, иногда имеет смысл провести предварительные специальные оценки).
Система (3.3) накладывает ограничения на рост переменной 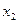 . Поскольку необходимо сохранять допустимость решений, т.е. все переменные должны оставаться неотрицательными, то должны выполняться следующие неравенства (при этом
. Поскольку необходимо сохранять допустимость решений, т.е. все переменные должны оставаться неотрицательными, то должны выполняться следующие неравенства (при этом 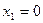 как неосновная переменная):
как неосновная переменная):
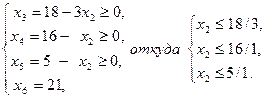
Каждое уравнение системы (3.3), кроме последнего, определяет оценочное отношение — границу роста переменной 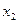 , сохраняющую неотрицательность соответствующей переменной. Эта граница определяется абсолютной величиной отношения свободного члена к коэффициенту при
, сохраняющую неотрицательность соответствующей переменной. Эта граница определяется абсолютной величиной отношения свободного члена к коэффициенту при 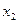 при условии, что эти числа имеют разные знаки. Последнее уравнение системы не ограничивает рост переменной
при условии, что эти числа имеют разные знаки. Последнее уравнение системы не ограничивает рост переменной 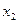 . так как данная переменная в него не входит (или формально входит с нулевым коэффициентом). В этом случае условимся обозначать границу символом
. так как данная переменная в него не входит (или формально входит с нулевым коэффициентом). В этом случае условимся обозначать границу символом 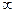 . Такой же символ будем использовать, когда свободный член и коэффициент при переменной в уравнении имеют одинаковые знаки, так как и в этом случае нет ограничений на рост переменной.
. Такой же символ будем использовать, когда свободный член и коэффициент при переменной в уравнении имеют одинаковые знаки, так как и в этом случае нет ограничений на рост переменной.
Не накладывает ограничений на рост переменной, переводимой в основные, и такое уравнение, где свободный член отсутствует (т.е. равен 0), а переводимая переменная имеет положительный коэффициент. И в этом случае граница обозначается символом 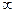 . Обратите внимание, что при нулевом свободном члене и отрицательном коэффициенте при переводимой переменной уравнение ограничивает рост этой переменной нулем! (любое положительное ее значение вносит отрицательную компоненту в следующее базисное решение).
. Обратите внимание, что при нулевом свободном члене и отрицательном коэффициенте при переводимой переменной уравнение ограничивает рост этой переменной нулем! (любое положительное ее значение вносит отрицательную компоненту в следующее базисное решение).
Очевидно, что сохранение неотрицательности всех переменных (допустимость решения) возможно, если не нарушается ни одна из полученных во всех уравнениях границ. В данном примере наибольшее возможное значение для переменной 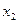 определяется как
определяется как  . При
. При 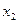 = 5 переменная
= 5 переменная 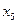 обращается в нуль и переходит в неосновные.
обращается в нуль и переходит в неосновные.
Уравнение, где достигается наибольшее возможное значение переменной, переводимой в основные (т.е. где оценка минимальна), называется разрешающим. В данном случае — это третье уравнение. Разрешающее уравнение будем выделять рамкой в системе ограничений.
II шаг. Основные переменные: 
Неосновные переменные: 
Выразим новые основные переменные через новые неосновные, начиная с разрешающего уравнения (его используем при записи выражения для 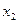 ):
):
 (3.4)
(3.4)
или
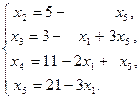
Второе базисное решение  = (0; 5; 3; 11; 0; 21) является допустимым и соответствует вершине А (0;5) на рис. 3.2. Геометрическая интерпретация перехода от
= (0; 5; 3; 11; 0; 21) является допустимым и соответствует вершине А (0;5) на рис. 3.2. Геометрическая интерпретация перехода от  к
к  — переход от вершины О к соседней вершине А на многоугольнике решений OABCDE. Выразив линейную функцию через неосновные переменные на этом шаге, получаем
— переход от вершины О к соседней вершине А на многоугольнике решений OABCDE. Выразив линейную функцию через неосновные переменные на этом шаге, получаем

Значение линейной функции F2 = F(Х2) = 15. Изменение значения линейной функции легко определить заранее как произведение наибольшего возможного значения переменной, переводимой в основные, на ее коэффициент в выражении для линейной функции; в данном случае 
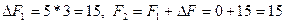 .
.
Однако значение  не является максимальным, так как повторяя рассуждения I шага, обнаруживаем возможность дальнейшего увеличения линейной функции за счет переменной х1, входящей в выражение для F с положительным коэффициентом. Система уравнений (3.4) определяет наибольшее возможное значение для
не является максимальным, так как повторяя рассуждения I шага, обнаруживаем возможность дальнейшего увеличения линейной функции за счет переменной х1, входящей в выражение для F с положительным коэффициентом. Система уравнений (3.4) определяет наибольшее возможное значение для 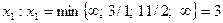 . Второе уравнение является разрешающим, переменная х3 переходит в неосновные, при этом
. Второе уравнение является разрешающим, переменная х3 переходит в неосновные, при этом 
III шаг. Основные переменные: 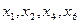 .
.
Неосновные переменные: 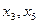 .
.
Как и на II шаге, выражаем новые основные переменные через новые неосновные, начиная с разрешающего уравнения (его используем при записи выражения для х1). После преобразований получаем

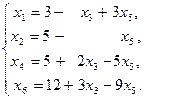 (3.5)
(3.5)
Базисное решение Х3= (3; 5; 0; 5; 0; 12) соответствует вершине В(3;5). Выражаем линейную функцию через неосновные переменные: 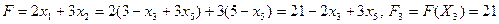 . Проверяем:
. Проверяем: 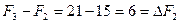 . Третье допустимое базисное решение тоже не является оптимальным, поскольку при неосновной переменной х5 в выражении линейной функции через неосновные переменные содержится положительный коэффициент. Переводим х5 в основную переменную. При определении наибольшего возможного значения для х5 следует обратить внимание на первое уравнение в системе (3.5), которое не дает ограничений на рост х5, так как свободный член и коэффициент при х3 имеют одинаковые знаки. Поэтому
. Третье допустимое базисное решение тоже не является оптимальным, поскольку при неосновной переменной х5 в выражении линейной функции через неосновные переменные содержится положительный коэффициент. Переводим х5 в основную переменную. При определении наибольшего возможного значения для х5 следует обратить внимание на первое уравнение в системе (3.5), которое не дает ограничений на рост х5, так как свободный член и коэффициент при х3 имеют одинаковые знаки. Поэтому 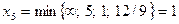 . Третье уравнение является разрешающим, и переменная х4 переходит в неосновные;
. Третье уравнение является разрешающим, и переменная х4 переходит в неосновные; 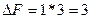 .
.
IV шаг. Основные переменные: 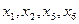
Неосновные переменные: 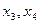
После преобразований получим:
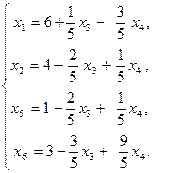
Базисное решение Х4 = (6; 4; 0; 0; 1; 3) соответствует вершине С(6; 4) на рис. 3.2.
Линейная функция, выраженная через неосновные переменные, имеет вид:  . Это выражение не содержит положительных коэффициентов при неосновных переменных, поэтому значение
. Это выражение не содержит положительных коэффициентов при неосновных переменных, поэтому значение  максимальное. Функцию F невозможно еще увеличить, переходя к другому допустимому базисному решению, т.е. решение Х4 оптимальное. Вспоминая экономический смысл всех переменных, можно сделать следующие выводы.
максимальное. Функцию F невозможно еще увеличить, переходя к другому допустимому базисному решению, т.е. решение Х4 оптимальное. Вспоминая экономический смысл всех переменных, можно сделать следующие выводы.
Прибыль предприятия принимает максимальное значение 24 руб. при реализации 6 единиц продукции  и 4 единиц продукции
и 4 единиц продукции 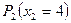 . Дополнительные переменные
. Дополнительные переменные 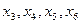 показывают разницу между запасами ресурсов каждого вида и их потреблением, т.е. остатки ресурсов. При оптимальном плане производства
показывают разницу между запасами ресурсов каждого вида и их потреблением, т.е. остатки ресурсов. При оптимальном плане производства  , т. е остатки ресурсов S1 и S2 равны нулю, а остатки ресурсов S3 и S4 равны соответственно 1 и 3 единицам.
, т. е остатки ресурсов S1 и S2 равны нулю, а остатки ресурсов S3 и S4 равны соответственно 1 и 3 единицам.
Теперь можно в общем виде сформулировать критерий оптимальности решения при отыскании максимума линейной функции: если в выражении линейной функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то решение оптимально.
Дата добавления: 2015-02-09; просмотров: 115; Мы поможем в написании вашей работы!; Нарушение авторских прав |