Нижняя и верхняя цена игры

⇐ ПредыдущаяСтр 13 из 17Следующая ⇒

Рассмотрим парную конечную игру. Пусть игрок А располагает т личными стратегиями, которые обозначим А₁, А₂,…, А_т. Пусть у игрока В имеется п личных стратегий, обозначим их В₁, В₂,…, В_п. Говорят, что игра имеет размерность т х п. В результате выбора игроками любой пары стратегий

А_i и B_j (i = 1, 2,…, т; j = 1, 2, .., п)

однозначно определяется исход игры, т.е. выигрыш а_ij игрока А (положительный или отрицательный) и проигрыш (-а_ij) игрока В. Предположим, что значения а_ij известны для любой пары стратегий (А_i , B_j). Матрица Р = (а_ij), i = 1, 2,…, т; j = 1, 2, .., п, элементами которой являются выигрыши, соответствующие стратегиям А_i и B_j называется платежной матрицей или матрицей игры. Общий вид такой матрицы представлен в табл. 6.1.

Строки этой таблицы соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В.

Составим платежную матрицу для следующей игры.

Таблица 6.1

B_i A_j	B₁	B₂	…	B_n
A₁	a₁₁	a₁₂	…	a_1n
A₂	a₂₁	a₂₂	…	a_2n
…	…	…	…	…
A_m	a_m1	a_m1	…	a_mn

6.1. Игра "поиск". Игрок А может спрятаться в одном из двух убежищ (I и II); игрок В ищет игрока А, и если найдет, то получает штраф 1 ден. ед. от А, в противном случае платит игроку А 1 ден. ед. Необходимо построить платежную матрицу игры.

Решение. Для составления платежной матрицы следует проанализировать поведение каждого из игроков. Игрок А может спрятаться в убежище I — обозначим эту стратегию через А₁ или в убежище II — стратегия A₂.

Игрок В может искать первого игрока в убежище I — стратегия B₁, либо в убежище II — стратегия B₂. Если игрок А находится в убежище I и там его обнаруживает игрок В, т.е. осуществляется пара стратегий (A₁, B₁), то игрок А платит штраф, т.е. a₁₁ = -1. Аналогично получаем a₂₂ = -1(A₂, B₂). Очевидно, что стратегии (A₁, B₂) и (A₂, B₁) дают игроку А выигрыш 1, поэтому a₁₂ = a₂₁ = 1. Таким образом, для игры "поиск" размера 2x2 получаем платежную матрицу

.►

Рассмотрим игру т х п с матрицей Р = (а_ij), i =1, 2,…, т; j =1, 2,…, п и определим наилучшую среди стратегий А₁, А₂,…, А_т. Выбирая стратегию А_i, игрок А должен рассчитывать, что игрок В ответит на нее той из стратегий B_j, для которой выигрыш для игрока А минимален (игрок В стремится "навредить" игроку А).

Обозначим через α_i, наименьший выигрыш игрока А при выборе им стратегии А_i, для всех возможных стратегий игрока В (наименьшее число в

i-й строке платежной матрицы), т.е.

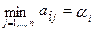(6.1)

Среди всех чисел α_i (i = 1, 2,…, т) выберем наибольшее: .

Назовем α нижней ценой игры, или максимальным выигрышем (максимином). Это гарантированный выигрыш игрока А при любой стратегии игрока В. Следовательно,

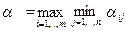. (6.2)

Стратегия, соответствующая максимину, называется максиминной стратегией. Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А; выбирая стратегию В_j он учитывает максимально возможный при этом выигрыш для А. Обозначим

. (6.3)

Среди всех чисел β_ij, выберем наименьшее 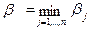и назовем β верхней ценой игры или минимаксным выигрышем (минимаксом). Это гарантированный проигрыш игрока В. Следовательно,

. (6.4)

Стратегия, соответствующая минимаксу, называется минимаксной стратегией.

Принцип, диктующий игрокам выбор наиболее "осторожных" минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника. Определим нижнюю и верхнюю цены игры и соответствующие стратегии в задаче 6.1.Рассмотрим платежную матрицу

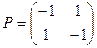
из задачи 6.1.При выборе стратегии А₁ (первая строка матрицы) минимальный выигрыш равен 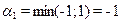и соответствует стратегии β₁ игрока В. При выборе стратегии A₂ (вторая строка матрицы) минимальный выигрыш равен , он достигается при стратегии B₂.

Гарантируя себе максимальный выигрыш при любой стратегии игрока В, т.е. нижнюю цену игры , игрок А может выбирать любую стратегию: А₁ или A₂, т.е. любая его стратегия является максиминной.

Выбирая стратегию В₁ (столбец 1), игрок В понимает, что игрок А ответит стратегией А₂, чтобы максимизировать свой выигрыш (проигрыш В). Следовательно, максимальный проигрыш игрока В при выборе им стратегии В₁равен .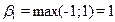

Аналогично максимальный проигрыш игрока В (выигрыш А) при выборе им стратегии B₂ (столбец 2) равен .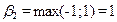

Таким образом, при любой стратегии игрока А гарантированный минимальный проигрыш игрока В равен - верхней цене игры.

Любая стратегия игрока В является минимаксной. Дополнив табл. 6.1 строкой β_j и столбцом α_i, получим табл. 6.2. На пересечении дополнительных строки и столбца будем записывать верхнюю и нижнюю цены игр.

Таблица 6.2

B_i A_j B₁ B₂ α_i

A₁ -1 1 -1

A₂ 1 -1 -1

β_j 1 1 α=1 β=1

В задаче 6.1,рассмотренной выше, верхняя и нижняя цены игры различны: α ≠ β.

Если верхняя и нижняя цены игры совпадают, то общее значение верхней и нижняя цены игры совпадают, то общее значение верхней и нижней цены игры α = β = v называется чистой ценой игры, или ценой игры. Минимаксные стратегии, соответствующие цене игры, являются оптимальными стратегиями, а их совокупность — оптимальным решением, или решением игры. В этом случае игрок А получает максимальный гарантированный (не зависящий от поведения игрока В) выигрыш v, а игрок В добивается минимального гарантированного (вне зависимости от поведения игрока А) проигрыша v. Говорят, что решение игры обладает устойчивостью, т.е. если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.

Пара чистых стратегий А_i и В_j дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент а_ij является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация, если она существует, называется седловой точкой (по аналогии с поверхностью седла, которая искривляется вверх в одном направлении и вниз — в другом).

6.2. Определить нижнюю и верхнюю цену игры, заданной платежной матрицей

.

Имеет ли игра седловую точку?

Таблица 6.3

B_j A_i B₁ B₂ B₃ α_i

A₁ 0,5 0,6 0,8 0,5

A₂ 0,9 0,7 0,8

0,7

A₃ 0,7 0,6 0,6 0,6

β_j 0,9

0,7

0,8 α = β=0,7

Решение. Все расчеты удобно проводить в таблице, к которой, кроме матрицы Р, введены столбец α_i и строка β_j (табл.6.3). Анализируя строки матрицы (стратегии игрока А), заполняем столбец α_i : α₁ = 0,5, α₂ = 0,7, α₃ = 0,6 — минимальные числа в строках 1, 2, 3. Аналогично β₁= 0,9, β₂ = 0,7, β₃ = 0,8 — максимальные числа в столбцах 1, 2, 3 соответственно. Нижняя цена игры (наибольшее число в столбце α_i) и верхняя цена игры (наименьшее число в строке β_j). Эти значения равны, т.е. α = β, и достигаются на одной и той же паре стратегий (A₂, B₂). Следовательно, игра имеет седловую точку (A₂, В₂) и цена игры v = 0,7.

Дата добавления: 2015-02-09; просмотров: 329; Мы поможем в написании вашей работы!; Нарушение авторских прав

⇐ Предыдущая 8 9 10 11 121314 15 16 17 Следующая ⇒

lektsii.com - Лекции.Ком - 2014-2024 год. (0.006 сек.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав
Главная страница Случайная страница Контакты