
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
РАСЧЕТ ПАРАМЕТРОВ КОДЕРА И ДЕКОДЕРА ПРОСТОГО КОДА
Предполагается, что кодирование ведется равномерным кодом, при котором, в отличие от неравномерного кода, более просты в реализации кодер и декодер.
Исходные данные:
- объем алфавита источника дискретных сообщений  ;
;
- скорость модуляции на выходе кодера простого кода В;
- допустимая вероятность ошибки знака на выходе декодера  .
.
Требуется определить:
- длительность двоичного символа (бита*) на выходе кодера  ;
;
- значность простого кода n;
- время передачи одного знака  ;
;
- допустимую вероятность ошибки бита на входе декодера  .
.
Длительность двоичного символа на выходе кодера определяется
 (3.1)
(3.1)
Значность кода определяется из условия, что число возможных комбинаций не меньше объема алфавита источника
 или
или 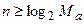 (3.2)
(3.2)
Поскольку другие требования к коду не предъявляются, то значность кода выбирается как минимальное целое число, при котором выполняются неравенства (3.2).
Время передачи одного знака
 (3.3)
(3.3)
Допустимая вероятность ошибки бита на входе декодера определяется при условии, что ошибки символов в канале связи (выход кодера - вход декодера) независимы:  . При
. При  .
.
Откуда  (3.4)
(3.4)
4. РАСЧЕТ ПАРАМЕТРОВ АЦП И ЦАП
Исходные данные для расчетов:
- максимальная частота спектра первичного сигнала  ;
;
- плотность вероятности мгновенных значений первичного сигнала p(b);
- средняя мощность первичного сигнала  ;
;
- коэффициент амплитуды первичного сигнала  ;
;
- допустимое отношение сигнал/помеха на входе получателя  ;
;
- допустимое значение сигнал/шум квантования  ;
;
- в АЦП производится равномерное квантование.
Требуется:
- составить и описать структурные схемы АЦП и ЦАП;
- определить интервал дискретизации  и частоту дискретизации
и частоту дискретизации 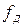 ;
;
- определить число уровней квантования L и значность двоичного кода n;
- рассчитать длительность двоичного символа  ;
;
- рассчитать отношение сигнал/шум квантования  при выбранных параметрах АЦП;
при выбранных параметрах АЦП;
- рассчитать допустимую вероятность ошибки символа  в канале связи (на входе ЦАП).
в канале связи (на входе ЦАП).
1. Структурные схемы АЦП и ЦАП подробно описаны в [1, гл.8; 2, гл.16]. Приведенные там схемы АЦП необходимо дополнить входным ФНЧ, который в реальных системах электросвязи используется для ограничения спектра первичного сигнала. Это связано с тем, что у большинства первичных сигналов спектр является медленно убывающей функцией, и величина  не есть частота, выше которой спектр равен нулю, а является граничной частотой полосы, которую необходимо передать из условия достижения заданного качества воспроизведения первичного сигнала (
не есть частота, выше которой спектр равен нулю, а является граничной частотой полосы, которую необходимо передать из условия достижения заданного качества воспроизведения первичного сигнала (  определяется требуемой разборчивостью речи, четкостью изображения и т.д.).
определяется требуемой разборчивостью речи, четкостью изображения и т.д.).
2. Интервал дискретизации по времени  выбирается на основе теоремы Котельникова [1, разд. 2.7; 2, разд. 2.4]. Обратная величина к
выбирается на основе теоремы Котельникова [1, разд. 2.7; 2, разд. 2.4]. Обратная величина к  - частота дискретизации
- частота дискретизации  выбирается из условия
выбирается из условия
 (4.1)
(4.1)
Увеличение частоты дискретизации позволяет упростить входной фильтр АЦП, ограничивающий спектр первичного сигнала, и выходной (интерполирующий) ФНЧ ЦАП, восстанавливающий непрерывный сигнал по отсчетам. Но увеличение частоты дискретизации приводит к уменьшению длительности двоичных сигналов на выходе АЦП, что требует нежелательного расширения полосы частот канала связи для передачи этих символов. Обычно параметры входного ФНЧ АЦП и выходного ФНЧ ЦАП выбирают одинаковыми.
На рис. 2 даны: 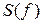 - спектр отсчетов, представленных узкими импульсами,
- спектр отсчетов, представленных узкими импульсами,  - спектр непрерывного сигнала
- спектр непрерывного сигнала  ,
,  - рабочее ослабление ФНЧ. Для того, чтобы ФНЧ не вносили линейных искажений в непрерывный сигнал, граничные частоты полос пропускания ФНЧ должны удовлетворять условию
- рабочее ослабление ФНЧ. Для того, чтобы ФНЧ не вносили линейных искажений в непрерывный сигнал, граничные частоты полос пропускания ФНЧ должны удовлетворять условию
 (4.2)
(4.2)
Для того, чтобы исключить наложение спектров  и
и  , а также обеспечить ослабление восстанавливающим ФНЧ составляющих
, а также обеспечить ослабление восстанавливающим ФНЧ составляющих  , граничные частоты полос задерживания ФНЧ должны удовлетворять условию
, граничные частоты полос задерживания ФНЧ должны удовлетворять условию
 . (4.3)
. (4.3)
Чтобы ФНЧ не были слишком сложными, отношение граничных частот выбирают из условия
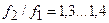 . (4.4)
. (4.4)
После подстановки соотношений (4.2) и (4.3) в (4.4) можно выбрать частоту 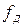 .
.

 Так, например, для речевых сигналов с
Так, например, для речевых сигналов с  =3400 Гц Международным Консультативным Комитетом по Телеграфии и Телефонии (МККТТ) рекомендовано значение
=3400 Гц Международным Консультативным Комитетом по Телеграфии и Телефонии (МККТТ) рекомендовано значение 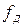 =8 кГц.
=8 кГц.
3. Помехоустойчивость системы передачи непрерывных сообщений определяется величиной
 (4.5)
(4.5)
где  - средняя мощность первичного сигнала;
- средняя мощность первичного сигнала;
 - средняя мощность помехи на выходе системы передачи.
- средняя мощность помехи на выходе системы передачи.
В системе цифровой передачи методом ИКМ мощность помехи на выходе ЦАП определяется
 , (4.6)
, (4.6)
где  - средняя мощность шума квантования;
- средняя мощность шума квантования;
 - средняя мощность шумов ложных импульсов.
- средняя мощность шумов ложных импульсов.
Если задано отношение сигнал/шум квантования  , то
, то
 . (4.7)
. (4.7)
Если же  не задано, а задано
не задано, а задано  , то полагают, что
, то полагают, что
 (4.8)
(4.8)
При проведении расчетов по формулам (4.5) и (4.7) заданные в децибелах отношения сигнал/помеха необходимо представить в разах
 . (4.9)
. (4.9)
Мощность шума квантования выражается через величину шага квантования  [1, ф-ла (8.8)]
[1, ф-ла (8.8)]
 . (4.10)
. (4.10)
Шаг квантования зависит от числа уровней квантования L
 (4.11)
(4.11)
Здесь предполагается, что первичный сигнал 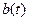 , подлежащий преобразованию в цифровой сигнал, принимает значения от
, подлежащий преобразованию в цифровой сигнал, принимает значения от  до
до  и интервал (
и интервал (  ,
,  ) подлежит квантованию. У сигналов со средним значением равным нулю
) подлежит квантованию. У сигналов со средним значением равным нулю  . Если значение
. Если значение  не задано, то оно определяется с помощью соотношения
не задано, то оно определяется с помощью соотношения
 (4.12)
(4.12)
где  - коэффициент амплитуды (в [1] обозначается П и называется пик-фактором). Он характеризует превышение максимальным (амплитудным) значением сигнала его среднеквадратического значения, равного корню из средней мощности сигнала.
- коэффициент амплитуды (в [1] обозначается П и называется пик-фактором). Он характеризует превышение максимальным (амплитудным) значением сигнала его среднеквадратического значения, равного корню из средней мощности сигнала.
На основе соотношений (4.10) и (4.11) минимально возможное число уровней квантования определяется
 (4.13)
(4.13)
Значность двоичного кода АЦП
 (4.14)
(4.14)
есть целое число. Поэтому число уровней квантования L выбирается как такая целая степень числа 2, при которой
 (4.15)
(4.15)
После выбора величины L необходимо рассчитать отношение сигнал/шум квантования [1, ф-ла (8.11)]
 (4.16)
(4.16)
4. Для определения допустимой вероятности ошибки двоичного символа на входе ЦАП  необходимо предварительно определить допустимую величину мощности шума ложных импульсов на основе соотношения (4.6)
необходимо предварительно определить допустимую величину мощности шума ложных импульсов на основе соотношения (4.6)
 (4.17)
(4.17)
Здесь  -мощность шума квантования, определяемая соотношениями (4.10) и (4.11) при выбранном числе уровней квантования L. Далее воспользуемся соотношением [1, ф-ла (8.14)], связывающим
-мощность шума квантования, определяемая соотношениями (4.10) и (4.11) при выбранном числе уровней квантования L. Далее воспользуемся соотношением [1, ф-ла (8.14)], связывающим  и вероятность ошибки бита на входе ЦАП
и вероятность ошибки бита на входе ЦАП 
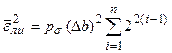 (4.18)
(4.18)
Величина шага квантования определяется формулой (4.11). Соотношение (4.18) позволяет рассчитать допустимую вероятность ошибки символа  на входе ЦАП.
на входе ЦАП.
Длительность двоичного символа на выходе АЦП определяется
 (4.19)
(4.19)
5. РАСЧЕТ ИНФОРМАЦИОННЫХ ХАРАКТЕРИСТИК ИСТОЧНИКА СООБЩЕНИЙ И ПЕРВИЧНЫХ СИГНАЛОВ
5.1 Расчет информационных характеристик источника непрерывных сообщений
Сообщение непрерывного источника преобразуется в первичный аналоговый сигнал 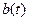 обычно без потери информации, поэтому расчеты информационных характеристик источника проводятся для первичного сигнала
обычно без потери информации, поэтому расчеты информационных характеристик источника проводятся для первичного сигнала
Исходные данные для расчета:
- плотность вероятности мгновенных значений первичного сигнала  ;
;
- максимальная частота спектра первичного сигнала  ;
;
- отношение средней мощности первичного сигнала к средней мощности ошибки воспроизведения на выходе системы передачи  .
.
Подлежат расчету:
- эпсилон-энтропия источника  ;
;
- коэффициент избыточности источника 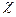 ;
;
- производительность источника  .
.
Сведения об эпсилон-энтропии и методах ее расчета даны в [1, разд. 4.7] - расчетная формула (4.63). Входящие в формулу (4.63) дифференциальная энтропия  и условная энтропия
и условная энтропия  вычисляются с помощью соотношения (4.30) в [1] при известных плотностях вероятности. Дифференциальная энтропия сигнала зависит от вида распределение вероятностей
вычисляются с помощью соотношения (4.30) в [1] при известных плотностях вероятности. Дифференциальная энтропия сигнала зависит от вида распределение вероятностей  и дисперсии сигнала
и дисперсии сигнала  , и соответствующие расчетные формулы для ее вычислений приведены в табл. 1. У сигналов со средним значением равным нулю
, и соответствующие расчетные формулы для ее вычислений приведены в табл. 1. У сигналов со средним значением равным нулю  .
.
При расчетах полагают, что ошибка воспроизведения на выходе системы передачи является гауссовской, и условная энтропия  вычисляется по формуле (4.34) в [1], в которую необходимо подставить значение дисперсии ошибки воспроизведения (мощности помехи на выходе системы передачи)
вычисляется по формуле (4.34) в [1], в которую необходимо подставить значение дисперсии ошибки воспроизведения (мощности помехи на выходе системы передачи)  . Значение
. Значение  определяется по заданному отношению сигнал/помеха
определяется по заданному отношению сигнал/помеха  и средней мощности сигнала
и средней мощности сигнала  по формуле (4.5).
по формуле (4.5).
Таблица 1. Дифференциальная энтропия для некоторых законов распределения случайных величин
| Распределение вероятности | Дифференциальная энтропия , бит/отсчет |
Нормальное распределение (рис. 3а)

|

|
Двустороннее экспоненциальное распределение (рис. 3б)

|

|
Равномерное распределение (рис. 3в)
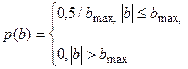
|

|

До вычислений заданное в децибелах отношение необходимо представить в разах - формула (4.9).
1. Коэффициент избыточности источника 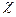 вычисляется по формуле (4.10) из [1]. В эту формулу подставляются вычисленное значение эпсилон-энтропии
вычисляется по формуле (4.10) из [1]. В эту формулу подставляются вычисленное значение эпсилон-энтропии  и максимально возможное значение
и максимально возможное значение 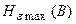 , достигаемое при нормальном распределении вероятности сигнала
, достигаемое при нормальном распределении вероятности сигнала 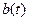 и той же дисперсии сигнала
и той же дисперсии сигнала  .
.
2. Производительность источника  , которую называют эпсилон-производительностью, вычисляют в предположении, что отсчеты следуют через интервал Котельникова - формула (4.67) из [1]. В этой формуле
, которую называют эпсилон-производительностью, вычисляют в предположении, что отсчеты следуют через интервал Котельникова - формула (4.67) из [1]. В этой формуле  - максимальная частота спектра первичного сигнала
- максимальная частота спектра первичного сигнала  . Требования к пропускной способности непрерывного канала связи формулируются на основе теоремы кодирования для канала с помехами [1, разд. 4.6].
. Требования к пропускной способности непрерывного канала связи формулируются на основе теоремы кодирования для канала с помехами [1, разд. 4.6].
5.2 Расчет информационных характеристик источника дискретных сообщений
Исходные данные для расчета:
- объем алфавита источника  ;
;
- вероятности знаков  , образующих алфавит источника (предполагается, что знаки в сообщениях независимы);
, образующих алфавит источника (предполагается, что знаки в сообщениях независимы);
- время передачи одного знака 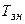 .
.
Подлежат расчету:
- энтропия источника  ;
;
- коэффициент избыточности источника 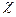 ;
;
- производительность источника  .
.
Расчеты информационных характеристик можно выполнить на основе материала, изложенного в разд. 4.1 учебника [1] . Необходимые для расчетов вероятности букв в украинском, русском и английском текстах приведены в табл. 2, 3 и 4. Расчеты энтропии источника следует выполнять на ЭВМ либо программируемом калькуляторе.
Таблица 2. Распределение вероятностей букв в украинских текстах
| Буква | Вероятность | Буква | Вероятность | Буква | Вероятность | Буква | Вероятность |
| Пробел | 0.122 | Р | 0.040 | З | 0.018 | Ж | 0.007 |
| О | 0.090 | С | 0.034 | И | 0.017 | Ц | 0.006 |
| А | 0.074 | Л | 0.034 | Б | 0.016 | Ю | 0.006 |
| И | 0.059 | К | 0.034 | Я | 0.015 | Ї | 0.006 |
| І | 0.055 | У | 0.032 | Г | 0.013 | Е | 0.003 |
| Н | 0.053 | Д | 0.026 | Ч | 0.012 | Ф | 0.002 |
| В | 0.047 | П | 0.026 | Ш | 0.010 | ||
| Т | 0.044 | М | 0.023 | Х | 0.008 | ||
| Е | 0.041 | Ь | 0.021 | Щ | 0.008 |
Таблица 3. Распределение вероятностей букв в русских текстах
| Буква | Вероят ность | Буква | Вероят ность | Буква | Вероят ность | Буква | Вероятность |
| Пробел | 0.175 | Р | 0.040 | Я | 0.018 | Х | 0.009 |
| О | 0.089 | В | 0.038 | Ы | 0.016 | Ж | 0.007 |
| Е,Ё | 0.072 | Л | 0.035 | З | 0.016 | Ю | 0.006 |
| А | 0.062 | К | 0.028 | Ь,Ъ | 0.014 | Ш | 0.006 |
| И | 0.062 | М | 0.026 | Б | 0.014 | Ц | 0.004 |
| Т | 0.053 | Д | 0.025 | Г | 0.013 | Щ | 0.003 |
| Н | 0.053 | П | 0.023 | Ч | 0.012 | Э | 0.003 |
| С | 0.045 | У | 0.021 | Й | 0.010 | Ф | 0.002 |
Таблица 4. Распределение вероятностей букв в английских текстах
| Буква | Вероят ность | Буква | Вероят ность | Буква | Вероят ность | Буква | Вероятность |
| Пробел | 0.198 | R | 0.054 | U | 0.022 | V | 0.008 |
| E | 0.105 | S | 0.052 | M | 0.021 | K | 0.003 |
| T | 0.072 | H | 0.047 | P | 0.017 | X | 0.002 |
| O | 0.065 | D | 0.035 | Y | 0.012 | J | 0.001 |
| A | 0.063 | L | 0.029 | W | 0.012 | Q | 0.001 |
| N | 0.059 | C | 0.023 | G | 0.011 | Z | 0.001 |
| I | 0.055 | F | 0.022 | B | 0.010 |
Производительность источника  легко определить, зная энтропию и время передачи одного знака [1, ф-ла (4.11)].
легко определить, зная энтропию и время передачи одного знака [1, ф-ла (4.11)].
Требования к пропускной способности дискретного канала связи формулируются на основе теоремы кодирования для канала с помехами [1, разд. 4.6].
5.3. Расчет информационных характеристик сигнала на выходе АЦП
Исходные данные для расчета:
- плотность распределения вероятностей мгновенных значений  и коэффициент амплитуды
и коэффициент амплитуды  первичного сигнала;
первичного сигнала;
- число уровней квантования АЦП L;
- частота дискретизации АЦП  .
.
Подлежат расчету:
- энтропия квантованных отсчетов  ;
;
- скорость создания информации на выходе АЦП  .
.
Квантованный сигнал  является дискретным по уровню и его энтропия
является дискретным по уровню и его энтропия  вычисляется по формуле (4.4) из [1] - формуле энтропии источника дискретных независимых сообщений (полагают, что производимые в АЦП отсчеты независимы).Входящие в эту формулу вероятности квантованных значений сигнала можно определить
вычисляется по формуле (4.4) из [1] - формуле энтропии источника дискретных независимых сообщений (полагают, что производимые в АЦП отсчеты независимы).Входящие в эту формулу вероятности квантованных значений сигнала можно определить
 , (5.1)
, (5.1)
где  - квантованное значение сигнала на i-ом уровне квантования;
- квантованное значение сигнала на i-ом уровне квантования;
 - плотность вероятности сигнала ;
- плотность вероятности сигнала ;
 - шаг квантования, определяемый по формуле (4.11).
- шаг квантования, определяемый по формуле (4.11).
Расчеты энтропии квантованного сигнала следует выполнять с помощью ЭВМ либо программируемого калькулятора.
Скорость создания информации на выходе квантующего устройства  вычисляется по формуле (4.11) из [1]. В эту формулу необходимо подставить значения энтропии квантованного сигнала и интервала дискретизации. Сравните значения
вычисляется по формуле (4.11) из [1]. В эту формулу необходимо подставить значения энтропии квантованного сигнала и интервала дискретизации. Сравните значения  и
и  и поясните причину их отличия.
и поясните причину их отличия.
6. РАСЧЕТ ПОМЕХОУСТОЙЧИВОСТИ ДЕМОДУЛЯТОРА
6.1. Расчет помехоустойчивости демодулятора сигнала аналоговой модуляции
Исходные данные:
- допустимое отношение сигнал/помеха на выходе демодулятора  ;
;
- вид модуляции;
- канал связи с постоянными параметрами и аддитивным белым гауссовским шумом со спектральной плотностью мощности  ;
;
- параметры первичного сигнала - коэффициент амплитуды  и максимальная частота спектра
и максимальная частота спектра  .
.
Подлежат расчету:
- зависимость  ;
;
- требуемое отношение средней мощности сигнала к удельной мощности шума 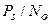 на входе демодулятора.
на входе демодулятора.
Основной характеристикой демодулятора сигнала аналоговой модуляции является зависимость  ,
,
где  - (6.1)
- (6.1)
отношение средних мощностей сигнала и помехи на выходе демодулятора;
 - (6.2)
- (6.2)
отношение средних мощностей сигнала и шума на входе демодулятора. Значения  и
и 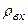 связывает величина g - выигрыш демодулятора [1, ф-ла (7.32)]:
связывает величина g - выигрыш демодулятора [1, ф-ла (7.32)]:
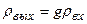 (6.3)
(6.3)
(здесь и ниже  и
и 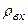 выражаются в разах).
выражаются в разах).
Для сигналов АМ, БМ и ОМ величина g определяется формулами, приведенными в [1, с. 220] (коэффициент амплитудной модуляции  подлежит выбору и обоснованию из условия, что
подлежит выбору и обоснованию из условия, что  ). Для заданного вида модуляции - ОМ, БМ или АМ определите выигрыш g и постройте график зависимости
). Для заданного вида модуляции - ОМ, БМ или АМ определите выигрыш g и постройте график зависимости  для диапазона значений
для диапазона значений  от 1 до допустимого значения. Масштаб для
от 1 до допустимого значения. Масштаб для  и
и 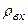 должен быть логарифмическим, как на рис. 7.5 в [1]. Определите требуемое отношение
должен быть логарифмическим, как на рис. 7.5 в [1]. Определите требуемое отношение 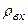 ; покажите на графике точку, соответствующую допустимому
; покажите на графике точку, соответствующую допустимому  и требуемому
и требуемому 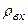 .
.
При частотной модуляции выигрыш определяется [1, ф-ла (7.42)]:
 (6.4)
(6.4)
где 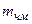 -индекс частотной модуляции;
-индекс частотной модуляции;
 - (6.5)
- (6.5)
коэффициент расширения полосы частот при ЧМ.
Формула (6.4) определяет выигрыш демодулятора при условии, что 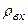 превышает пороговое отношение сигнал/шум
превышает пороговое отношение сигнал/шум  [1, разд. 7.5]. Зависимость же
[1, разд. 7.5]. Зависимость же  при любых
при любых 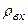 , включая область порога, достаточно сложная. Выражение, описывающее эту зависимость, можно получить на основе импульсной теории порога [3, с. 74…80]:
, включая область порога, достаточно сложная. Выражение, описывающее эту зависимость, можно получить на основе импульсной теории порога [3, с. 74…80]:
 (6.6)
(6.6)
Входящая в выражение величина 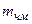 не известна и подлежит выбору. При выборе
не известна и подлежит выбору. При выборе 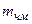 следует учитывать, что для увеличения помехоустойчивости демодулятора (выигрыша) необходимо увеличивать
следует учитывать, что для увеличения помехоустойчивости демодулятора (выигрыша) необходимо увеличивать 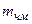 . Но при увеличении
. Но при увеличении 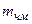 уменьшается
уменьшается 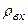 , определяемое соотношением (6.2) и равное при ЧМ
, определяемое соотношением (6.2) и равное при ЧМ
 .
.
Недопустимо, чтобы 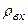 были меньше
были меньше  . Поэтому значение индекса
. Поэтому значение индекса 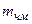 ограничено сверху условием работы демодулятора выше порога. Решить уравнение (6.6) относительно
ограничено сверху условием работы демодулятора выше порога. Решить уравнение (6.6) относительно 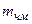 , положив
, положив 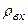 =
=  , а
, а  равным допустимому, не удается, так как значение
равным допустимому, не удается, так как значение  не известно, поскольку оно зависит от величины
не известно, поскольку оно зависит от величины 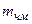 . Рекомендуется следующий порядок определения
. Рекомендуется следующий порядок определения 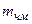 . Ориентировочное значение
. Ориентировочное значение  =10. Полагая, что
=10. Полагая, что 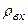 =10,
=10,  =2
=2 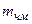 , и, используя соотношения (6.3) и (6.4), можно определить ориентировочное значение
, и, используя соотношения (6.3) и (6.4), можно определить ориентировочное значение 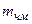 , при котором демодулятор будет работать в области порога:
, при котором демодулятор будет работать в области порога:
 ;
;  . (6.7)
. (6.7)
Затем, используя выражение (6.6), строят графики 5 зависимостей  для значения
для значения 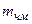 , полученного выше, и значений
, полученного выше, и значений 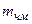
 и
и 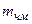
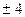 . По полученным зависимостям определяют значение
. По полученным зависимостям определяют значение 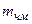 , при котором
, при котором  равно допустимому, а
равно допустимому, а 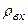 находится в области или несколько выше порога.
находится в области или несколько выше порога.
Если же полоса пропускания канала связи  задана, то значение
задана, то значение 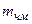 должно удовлетворять условию ограниченности полосы частот канала связи
должно удовлетворять условию ограниченности полосы частот канала связи
 . (6.8)
. (6.8)
Решив уравнение (6.8) относительно 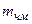 , получают
, получают 
, удовлетворяющее условию (6.8).
Окончательно выбирают 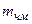 , как меньшее из
, как меньшее из  и
и  . Для выбранного значения
. Для выбранного значения 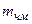 строят график
строят график  , если для этого
, если для этого 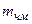 раньше график не был рассчитан. На этом графике указывают точку, соответствующую заданному
раньше график не был рассчитан. На этом графике указывают точку, соответствующую заданному 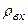 и требуемому
и требуемому  .
.
Найденное для АМ, БМ, ОМ, ЧМ отношение  , где
, где  - мощность шума, определяемая в полосе частот модулированного сигнала
- мощность шума, определяемая в полосе частот модулированного сигнала 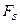 , позволяет определить требуемое отношение
, позволяет определить требуемое отношение
 (6.9)
(6.9)
на входе демодулятора. Ширина спектра модулированного сигнала определяется следующими соотношениями:
при ОМ  ;
;
при БМ и АМ  ; (6.10)
; (6.10)
при ЧМ  .
.
6.2. Расчет помехоустойчивости демодулятора сигнала дискретной модуляции
Исходные данные:
- вид модуляции и способ приема;
- канал связи с постоянными параметрами и аддитивным белым гауссовским шумом со спектральной плотностью мощности 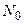 ;
;
- допустимая вероятность ошибки двоичного символа (бита) в канале  ;
;
- длительность двоичного символа 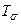 .
.
Требуется рассчитать:
- зависимость вероятности ошибки бита от отношения сигнал/шум на входе демодулятора  и построить график этой зависимости;
и построить график этой зависимости;
- значения требуемых отношений сигнал/шум на входе демодулятора  и
и  , обеспечивающих допустимую вероятность ошибки бита
, обеспечивающих допустимую вероятность ошибки бита  .
.
Помехоустойчивость демодулятора сигнала дискретной модуляции определяют вероятностью ошибки сигнала  либо вероятностью ошибки двоичного символа р. Вероятности ошибки
либо вероятностью ошибки двоичного символа р. Вероятности ошибки  и р зависят от вида модуляции, способа приема, отношения энергии сигнала к удельной мощности помехи и характеристик канала связи.
и р зависят от вида модуляции, способа приема, отношения энергии сигнала к удельной мощности помехи и характеристик канала связи.
Для двоичных сигналов  и р совпадают. Формулы для расчета вероятности ошибки символа при передаче двоичных сигналов по гауссовскому каналу связи с постоянными параметрами приведены в [1, разд. 6.5, 6.6; 2, табл. 15.2].
и р совпадают. Формулы для расчета вероятности ошибки символа при передаче двоичных сигналов по гауссовскому каналу связи с постоянными параметрами приведены в [1, разд. 6.5, 6.6; 2, табл. 15.2].
В табл. 5 приведены формулы, определяющие вероятность ошибки двоичного символа при передаче многопозиционных сигналов по гауссовскому каналу связи с постоянными параметрами. Сначала были получены формулы вероятности ошибки сигнала  путем суммирования вероятностей попадания суммы
путем суммирования вероятностей попадания суммы 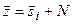 в области сигналов
в области сигналов  ,
,  ,
,  . Затем был произведен пересчет
. Затем был произведен пересчет  в р, в предположении, что используется манипуляционный код Грея.
в р, в предположении, что используется манипуляционный код Грея.
Таблица 5. Вероятности ошибки для различных способов приёма модулированных сигналов
| Способ приема | Вид модуляции | Вероятность ошибки двоичного кода |
| Коге-рентный | ФМ-4 | 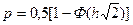
|
| ОФМ-4 | 
| |
| КАМ-16 | 
| |
| Некоге-рентный | ЧМ-М |  ; ; 
|
Во всех формулах приняты обозначения:
 - отношение энергии сигнала, затрачиваемой на передачу одного двоичного символа
- отношение энергии сигнала, затрачиваемой на передачу одного двоичного символа  к удельной мощности шума
к удельной мощности шума 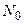 ;
;
 ;
;
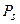 - средняя мощность сигнала;
- средняя мощность сигнала;
 - длительность двоичного символа.
- длительность двоичного символа.

 - функция Крампа.
- функция Крампа.
Можно пользоваться формулой аппроксимации функции Крампа.
 .
.
Для заданного вида модуляции и способа приема необходимо рассчитать и построить график зависимости  . При построении графика масштаб для р должен быть логарифмическим, а для значений
. При построении графика масштаб для р должен быть логарифмическим, а для значений  , выраженных в децибелах
, выраженных в децибелах  , - линейный. При расчетах увеличивают
, - линейный. При расчетах увеличивают  с шагом дБ от 2 дБ до тех пор, пока р не окажется меньше значения
с шагом дБ от 2 дБ до тех пор, пока р не окажется меньше значения  . Пример рассчитываемой зависимости дан на рис. 4 (приложение А) - кривая
. Пример рассчитываемой зависимости дан на рис. 4 (приложение А) - кривая  .
.
Если в канале связи не используется помехоустойчивое кодирование, то допустимая вероятность ошибки символа на выходе демодулятора равняется значению  , найденному при расчете параметров ЦАП либо декодера простого кода. Определите требуемое отношение сигнал/шум для системы передачи без кодирования
, найденному при расчете параметров ЦАП либо декодера простого кода. Определите требуемое отношение сигнал/шум для системы передачи без кодирования  , при котором
, при котором  . Покажите на графике значения
. Покажите на графике значения  и
и  . Рассчитайте требуемое при этом отношение
. Рассчитайте требуемое при этом отношение  на входе демодулятора
на входе демодулятора
 . (6.15)
. (6.15)
В случае модуляции АМ-2, при которой один из сигналов равен нулю, а сигналы равновероятны, отношение сигнал/шум определяется
 (6.16)
(6.16)
7. ВЫБОР КОРРЕКТИРУЮЩЕГО КОДА И РАСЧЕТ ПОМЕХОУСТОЙЧИВОТИ СИСТЕМЫ СВЯЗИ С КОДИРОВАНИЕМ
Корректирующие коды позволяют повысить помехоустойчивость и тем самым уменьшить требуемое отношение сигнал/шум на входе демодулятора при заданной вероятности ошибки передаваемых символов. Величина, показывающая во сколько раз (на сколько дБ) уменьшается требуемое кодирование, называется энергетическим выигрышем кодирования (ЭВК).
Каналы связи с помехоустойчивым кодированием и без него удобно сравнивать, если в качестве отношения сигнал/шум использовать отношение энергии сигнала, затрачиваемой на передачу одного информационного символа  , к удельной мощности шума
, к удельной мощности шума 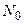 :
:
 (7.1)
(7.1)
Так, если в канале связи без кодирования требуемое отношение сигнал/шум для обеспечения заданной вероятности ошибки обозначим  , а в канале связи с кодированием -
, а в канале связи с кодированием -  , то ЭВК будет определяться
, то ЭВК будет определяться
 или
или  . (7.2)
. (7.2)
Исходные данные для расчета:
- требуемый ЭВК;
- вид модуляции в канале связи и способ приема;
- тип непрерывного канала связи;
- допустимая вероятность ошибки двоичного символа на выходе декодера  ;
;
- отношение сигнал/шум на входе демодулятора  , обеспечивающее допустимую вероятность ошибки
, обеспечивающее допустимую вероятность ошибки  в канале кодирования;
в канале кодирования;
- длительность двоичного символа на входе кодера корректирующего кода 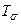 .
.
Требуется:
- выбрать и обосновать параметры кода: значность п, число информационных символов кодовой комбинации k и кратность исправляемых ошибок  ;
;
- рассчитать зависимость вероятности ошибки символа на выходе декодера от отношения сигнал/шум на входе демодулятора 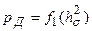 при использовании выбранного кода;
при использовании выбранного кода;
- определить полученный ЭВК;
- вычислить требуемое отношение  на входе демодулятора.
на входе демодулятора.
Прежде всего рассмотрим методику расчета помехоустойчивости канала связи с корректирующим кодом. Предположим, что параметры кода п, k и  и отношение сигнал/шум
и отношение сигнал/шум  заданы. При декодировании с исправлением ошибок вероятность ошибочного декодирования определяется из условия, что число ошибок в кодовой комбинации на входе декодера q превышает кратность исправляемых ошибок [1, ф-ла (5.15)]:
заданы. При декодировании с исправлением ошибок вероятность ошибочного декодирования определяется из условия, что число ошибок в кодовой комбинации на входе декодера q превышает кратность исправляемых ошибок [1, ф-ла (5.15)]:
 , (7.3)
, (7.3)
где  - (7.4)
- (7.4)
вероятность ошибки кратности q
 - (7.5)
- (7.5)
число сочетаний из п по q;
р - вероятность ошибки двоичного символа на входе декодера, расчет которой для гауссовского канала связи с постоянными параметрами рассмотрен в разд. 6.2. В используемые там формулы необходимо подставлять
 . (7.6)
. (7.6)
Соотношение (7.6) учитывает уменьшение длительности символов, передаваемых по непрерывному каналу связи, из-за введения в кодовые комбинации дополнительных символов при кодировании, и соответствующее уменьшение энергии сигнала на входе демодулятора.
Для перехода от вероятности ошибочного декодирования 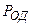 к вероятности ошибки двоичного символа
к вероятности ошибки двоичного символа  достаточно учесть принцип исправления ошибок декодером: декодер запрещенную кодовую комбинацию заменяет ближайшей разрешенной. Поэтому, если число ошибок в комбинации q=
достаточно учесть принцип исправления ошибок декодером: декодер запрещенную кодовую комбинацию заменяет ближайшей разрешенной. Поэтому, если число ошибок в комбинации q=  ,но
,но  , то в результате декодирования комбинация будет содержать
, то в результате декодирования комбинация будет содержать 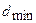 ошибок (
ошибок ( 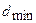 - кодовое расстояние кода). Поскольку ошибки более высокой вероятности маловероятны, то окончательно можно считать, что в ошибочно декодированной комбинации имеется
- кодовое расстояние кода). Поскольку ошибки более высокой вероятности маловероятны, то окончательно можно считать, что в ошибочно декодированной комбинации имеется 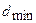 ошибочных символов. У корректирующих кодов кодовое расстояние
ошибочных символов. У корректирующих кодов кодовое расстояние  . С учетом этого переход от
. С учетом этого переход от 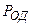 к
к  можно выполнить по формуле
можно выполнить по формуле
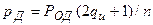 (7.7)
(7.7)
Приведенные соотношения позволяют выполнить расчет помехоустойчивости в канале связи с корректирующим кодом при заданных параметрах кода п, k и  , отношении сигнал/шум в непрерывном канале связи
, отношении сигнал/шум в непрерывном канале связи  , виде модуляции, способе приема и длительности символа
, виде модуляции, способе приема и длительности символа 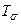 в следующем порядке:
в следующем порядке:
1. Расчет отношения сигнал/шум  на входе демодулятора по формуле (7.6);
на входе демодулятора по формуле (7.6);
2. Расчет вероятности ошибки символа на выходе демодулятора р по методике, изложенной в разд. 6.2;
3. Расчет вероятности ошибочного декодирования кодовой комбинации 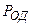 по формулам (7.3)…(7.5);
по формулам (7.3)…(7.5);
4. Расчет вероятности ошибки символа на выходе декодера  по формуле (7.7).
по формуле (7.7).
Согласно заданию на курсовую работу требуется выбрать и обосновать параметры кода, обеспечивающего требуемый ЭВК. Перейдем к решению этой задачи.
Чем больше кратность исправляемых ошибок  , тем более высокая помехоустойчивость может быть достигнута за счет применения кодирования. Но при увеличении
, тем более высокая помехоустойчивость может быть достигнута за счет применения кодирования. Но при увеличении  растет сложность кодера и особенно декодера. Рассмотрим применение кодов с наименьшим значением
растет сложность кодера и особенно декодера. Рассмотрим применение кодов с наименьшим значением  =1 и, соответственно, с
=1 и, соответственно, с 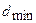 =3.
=3.
Для любого натурального числа r=n-k существует код Хемминга с 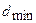 =3 при
=3 при  [1, с. 149]. К кодам Хемминга любой длины п с наименьшим числом r, удовлетворяющим условию
[1, с. 149]. К кодам Хемминга любой длины п с наименьшим числом r, удовлетворяющим условию
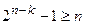 (7.8)
(7.8)
Используя соотношение (7.8) можно указать пару чисел n и k, при которых существует код Хемминга. При увеличении n имеет место следующее: увеличивается скорость кода  , увеличивается отношение сигнал/шум
, увеличивается отношение сигнал/шум  (ф-ла (7.6)) на входе демодулятора при фиксированном значении
(ф-ла (7.6)) на входе демодулятора при фиксированном значении  , уменьшается вероятность ошибки символа на входе декодера р. При малых значениях р и не слишком больших значениях п величина
, уменьшается вероятность ошибки символа на входе декодера р. При малых значениях р и не слишком больших значениях п величина  убывает быстрее, нежели растет число
убывает быстрее, нежели растет число  , и величины
, и величины 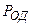 и
и  уменьшаются. Следовательно, при увеличении п увеличивается ЭВК. При больших значениях п уменьшение
уменьшаются. Следовательно, при увеличении п увеличивается ЭВК. При больших значениях п уменьшение  замедляется и при достаточно больших значениях п начинается рост
замедляется и при достаточно больших значениях п начинается рост  и уменьшение ЭВК. Значения ЭВК для
и уменьшение ЭВК. Значения ЭВК для  ,
,  и
и  приведены на рис.5а при когерентном и на рис.5б (приложение Д) при некогерентном способе приема в канале связи.
приведены на рис.5а при когерентном и на рис.5б (приложение Д) при некогерентном способе приема в канале связи.
После набора кода следует рассчитать зависимость, характеризующую помехоустойчивость канала связи с кодированием. Для этого изменяют величину  в широких пределах, чтобы величина
в широких пределах, чтобы величина  принимала значения от 0.1 до значения, которое несколько меньше
принимала значения от 0.1 до значения, которое несколько меньше  , строят зависимость
, строят зависимость 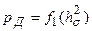 (рис.4), характеризующую помехоустойчивость канала связи с выбранным кодом. По этой зависимости определяют требуемое отношение сигнал/шум
(рис.4), характеризующую помехоустойчивость канала связи с выбранным кодом. По этой зависимости определяют требуемое отношение сигнал/шум  на входе демодулятора, при котором обеспечивается допустимая вероятность ошибки символа на выходе декодера, т.е.
на входе демодулятора, при котором обеспечивается допустимая вероятность ошибки символа на выходе декодера, т.е.  . По найденному значению
. По найденному значению  и полученному при расчете помехоустойчивости демодулятора значению
и полученному при расчете помехоустойчивости демодулятора значению  определяют ЭВК по формуле (7.2).
определяют ЭВК по формуле (7.2).
Следует также определить требуемое отношение сигнал/шум на входе демодулятора в канале связи с кодированием
 (7.10)
(7.10)
В случае модуляции АМ-2, при которой один из сигналов равен нулю, а сигналы равновероятны, отношение сигнал/шум определяется
 (7.11)
(7.11)
8. РАСЧЕТ ЭФФЕКТИВНОСТИ СИСТЕМЫ СВЯЗИ
Эффективность системы связи оценивают коэффициентами информационной, частотной и энергетической эффективности, определяемыми формулами (10.1)…(10.3) в [1]. Эти формулы определяют эффективность использования соответственно пропускной способности канала связи С, полосы пропускания канала связи  и отношения сигнал/шум
и отношения сигнал/шум  на выходе канала связи при заданном качестве воспроизведения передаваемого сообщения (
на выходе канала связи при заданном качестве воспроизведения передаваемого сообщения (  - скорость передачи информации). При расчетах эффективности под каналом связи понимают совокупность средств, обеспечивающих передачу сигналов от выхода модулятора до входа демодулятора.
- скорость передачи информации). При расчетах эффективности под каналом связи понимают совокупность средств, обеспечивающих передачу сигналов от выхода модулятора до входа демодулятора.
Исходные данные для расчета:
- тип канала связи - канал с постоянными параметрами и аддитивным белым гауссовским шумом;
- метод модуляции и параметры, определяющие ширину спектра модулированного сигнала и полосу пропускания канала связи;
- отношение  на выходе канала связи, при котором обеспечивается заданное качество воспроизведения сообщения;
на выходе канала связи, при котором обеспечивается заданное качество воспроизведения сообщения;
- скорость передачи информации.
Пропускная способность непрерывного канала связи определяется формулой Шеннона (4.48) в [1]. Входящая в эту формулу полоса пропускания канала связи  принимается равной ширине спектра модулированного сигнала
принимается равной ширине спектра модулированного сигнала 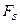 .
.
При передаче сигналов аналоговой модуляции ширина спектра сигналов определяется формулами (6.10).
При передаче сигналов дискретной модуляции минимально возможная ширина спектра сигналов определяется пределом Найквиста [1, с.284]: при АМ, ФМ, ОФМ и КАМ
 , (8.1)
, (8.1)
независимо от числа позиций сигнала М, а при ЧМ
 , (8.2)
, (8.2)
где  - (8.3)
- (8.3)
длительность элемента модулированного сигнала;
 - длительность двоичного символа на входе демодулятора.
- длительность двоичного символа на входе демодулятора.
Если передаваемое сообщение не подвергается помехоустойчивому кодированию, то значение  равно длительности двоичного символа
равно длительности двоичного символа 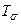 на выходе АЦП либо кодера простого кода. Если же используется помехоустойчивое кодирование, то
на выходе АЦП либо кодера простого кода. Если же используется помехоустойчивое кодирование, то
 , (8.4)
, (8.4)
где n и k - параметры корректирующего кода.
Пропускную способность непрерывного канала связи следует рассчитать для всех рассмотренных в курсовой работе вариантов передачи непрерывных сообщений: вариант аналоговой передачи и 2 варианта цифровой передачи - с помехоустойчивым кодированием и без него.
Сопоставьте полученные значения пропускной способности канала связи С с производительностью источника  , найденную при расчете информационных характеристик источника сообщений. Что утверждает теорема Шеннона о таком соотношении
, найденную при расчете информационных характеристик источника сообщений. Что утверждает теорема Шеннона о таком соотношении  и С [1, разд. 4.6]?
и С [1, разд. 4.6]?
Для расчета эффективности скорость передачи информации 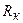 можно принять равной производительности источника
можно принять равной производительности источника  - при том качестве воспроизведения сообщений, которое имеет место в рассчитываемой системе связи, потери информации пренебрежимо малы. Коэффициенты эффективности следует рассчитать для всех вариантов передачи.
- при том качестве воспроизведения сообщений, которое имеет место в рассчитываемой системе связи, потери информации пренебрежимо малы. Коэффициенты эффективности следует рассчитать для всех вариантов передачи.
Необходимо рассчитать и построить график предельной зависимости  - предел Шеннона [1, рис. 11.1].Значения
- предел Шеннона [1, рис. 11.1].Значения 
 и
и  откладывают в логарифмических единицах - соответственно
откладывают в логарифмических единицах - соответственно 
Дата добавления: 2015-02-09; просмотров: 705; Мы поможем в написании вашей работы!; Нарушение авторских прав |