Встраиваемые и рекурсивные

Цель работы : Изучение функций в языке С++.

Задание: Составить алгоритм и написать программу на языке С++ решения задачи согласно своего варианта.

Длительность:2 часа.

Теоретические основы:

Встраиваемые (inline-) функции

В результате работы компилятора каждая функция представляется в виде машинного кода. Если в программе вызов функции встречается несколько раз, в местах таких обращений генерируются коды вызова уже реализованного экземпляра функции. Однако выполнение вызовов требует некоторой затраты времени. Таким образом, если тело функции небольшого размера и обращение к ней в программе происходит довольно часто, на практике можно указать компилятору вместо вызовов функции в соответствующих местах генерировать все ее тело. Осуществляется это с помощью ключевого слова inline.Тем самым увеличивается производительность реализованного кода, хотя, конечно, размер программы может увеличиваться. Компиляторы различных фирм накладывают свои ограничения на использование встраиваемых функций, поэтому перед использованием inline, функций необходимо обратиться к руководству компилятора.

Ключевое слово inline должно предшествовать первому вызову встраиваемой функции (например, содержаться в ее прототипе).

#include <iostream.h>

// Прототип встраиваемой функции:

inline int Sum (int, int);

int main ()

{

int A = 2; B = 6; C = 3;

char eol = '\n';

// Вызовы встраиваемой функции,

// генерируют все тело функции

cout << Sun(A, B) << eol;

cout << Sun(B, C) << eol;

cout << Sun(A, C) << eol;

return 0;

}

int Sum (int x, int y);

{

return x+y;

}

В приведенном примере в каждом месте вызова функции Sum() будет сгенерирован код тела всей функции.

Рекурсивные функции

Как уже упоминалось ранее, функция может вызывать сама себя. При этом говорят, что возник рекурсивный вызов. Рекурсия бывает:

• простой - если функция в теле содержит вызов самой себя;
• косвенной - если функция вызывает другую функцию, а та в свою очередь вызывает первую.

При выполнении рекурсии программа сохраняет в стеке значения всех локальных переменных функции и ее аргументов, с тем чтобы в дальнейшем по возвращении из рекурсивного вызова восстановить их сохраненные значения.

В связи с вышеизложенным, применять рекурсию следует с осторожностью, так как ее использование для функций, содержащих большое количество переменных или слишком большое число рекурсивных вызовов, может вызвать переполнение стека. Следует также помнить, что при использовании рекурсивного вызова разработчик обязан предусмотреть механизм возврата в вызывающую процедуру, чтобы не произошло образования бесконечного цикла.

Некоторые задачи на практике могут быть проще и нагляднее решены именно с использованием рекурсивных функций. Например, решение тривиальной задачи нахождения факториала без обращения к рекурсии могло бы выглядеть следующим образом:

#include <iostream.h>

int main ()

{

int count = 1;

long int result = 1;

while (count && count < 13)

{

cout << "Введите целое число: ";

cin >> count;

for (int i=count; i>1; i--)

{

result *= i;

}

count << result << '\n';

result = 1;

}

return 0;

}

Ту же задачу можно решить более элегантно, применив рекурсию:

#include <iostream.h>

long int fact (long);

int main ()

{

int count = 1;

while (count && count < 31)

{

cout << "Введите целое число: ";

cin >> count;

cout << fact (count) << '\n';

}

return 0;

}

long int fact (long x)

{

if (x == 0 || x == 1)

return 1;

return x * fact(x-1);

}

Как видно, тело функции main () во втором примере максимально упростилось и занимается фактически вводом значения и выводом результата, в то время как все вычисления возложены на единственную содержательную строку в рекурсивной функции fact().

Задания по вариантам к лабораторной работе №5:

1. Составить подпрограмму вычисления длины дуги

образованной функцией f(х) в интервале (а, b). Используя подпрограмму, определить самую длинную из дуг, образованных функциями

f(х) = х² + 21п(1 + х²);

f(х) = х*1п|х²-2х|;

f(х) = (х² + 2х - b)е^-x

на интервале (2; 4); n = 50.

2. Составить подпрограмму определения минимума функции у = f(х), заданной в дискретных точках отрезка [а, b] с постоянным шагом h. Используя ее, найти минимумы функций:

y₁ = sin²х * соsх – 1n|х| на отрезке [0.1; 1], h = 0.1;

y₂ = x² - 2х + 8 на отрезке [-1; 1 ], h = 0.2.

3. Составить подпрограмму для определения максимума функции у = f(х), заданной в дискретных, точках отрезка [а, b] с постоянным шагом h. Используя ее, найти максимумы функций:

y₁ = е^х*соs²х - 1 на отрезке [1; 2], h = 0.1;

у₂ = х*1n|х + 1| на отрезке [0; 2], h = 0.2.

4. Составить подпрограмму определения минимума функции z = f(х, у), заданной в дискретных точках х_i =х₀ + ih_х; у_i = у₀ +jh_У (i = 1, 2,..., n_x; j=1, 2,.... n_у). Используя ее, найти минимумы функций:

z₁ = 3х² - 2у² + 4ху - 8х; х₀ = 1; h_х = 0.2; n_х = 10; у₀ = 2; h_у = 0.1; n_у = 20;

z₂ = 6х² + у²-4х-6у + 1; х₀ = 0; h_х = 0.1;n_x = 15;у₀ = -1; h_у = 0.1; n_у = 10.

5. Составить подпрограмму определения максимума функции z = f(х, у), заданной в дискретных точках х_i =х₀ + ih_х; у_i = у₀ +jh_У (i = 1, 2,..., n_x; j=1, 2,.... n_у). Используя ее, найти максимумы функций:

z₁ = х³ + у² - 2ху + 2; х₀ = 0; h_x = 0.1; n_x = 10; у₀ = 0; h_у = 0,1; n_у = 10;

z₂ = 2х³ + 3у² + 2х + 3у - 3ху; х₀ = 0; h_х = 0.2; n_x = 20; у₀ = 1; h_у = 0.1; n_у = 5.

6. Составить подпрограмму вычисления определенного интеграла по формуле прямоугольников

и, используя ее, вычислить

при расчетах принять n=20.

7. Составить подпрограмму вычисления площади треугольника, заданного координатами своих вершин, по

формуле , где р = (х+у+г)/2; х, у, z - длины сторон треугольника., определяемые расстояниями между вершинами треугольника. Найти суммарную площадь двух треугольников с вершинами (4, 5); (1,6); (6, 1)и(3, 3); (1, 7); (7, 1).

8. Составить подпрограмму вычисления числа сочетаний из n по m по формуле:

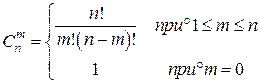
где значение факториала k! вычисляется с использованием подпрограммы-функции. Найти значение суммы , где а = 0.1; b = 0.9; n = 6.

9. Составить подпрограмму вычисления коэффициента корреляции двух случайных величин X и У на основании выборок X=(x₁, x₂, …, x_n), Y=(y₁, y₂, …, y_n) по формуле:

Для вычисления среднего арифметического вектора (z₁, z₂, …, z_n) по формуле

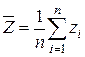
использовать подпрограмму-функцию. Найти для выборок

Х = (1; 1.2; 4.6; 2.5; 1.5; 3.8; 3.9), У = (0.5; 1.2; 3.8; 2.5; 4.2; 0.7; 1.5).

10. Составить подпрограмму вычисления высот треугольника со сторонами а, b, c.по формулам:

где р = (a+b+c)/2, если заданы координаты вершин треугольника. Для вычисления длин сторон а, b, с использовать подпрограмму определения длины отрезка между двумя точками. Найти меньшую из высот треугольника, имеющего следующие координаты вершин: (1, 2), (8, 7), (4, 0).

11. Составить подпрограмму определения координат точки пересечения двух прямых у = k₁х + b₁ и у = k₂х + b₂, проходящих через заданные точки по формулам:

Коэффициенты k и b прямой у = kх + b, проходящей через точки (х1, у1), (х2, у2), определить из уравнения:

Найти точки пересечения прямых, проходящих через точки (2, 4), (,7, 8) и (1, 8), (8, 2).

12. Составить подпрограмму вычисления составляющих вектора градиента функции F=(x₁, x₂, …, x_n) n переменных в точке x=(x₁, x₂, …, x_n) по конечно-разностным формулам

Найти вектор градиента в точке X = (4, 6) для функций

Z₁ = 2х² - 4у² + 8ху - 2х + 1;

Z₂ = 8х²у - 2ху

при .

13. Составить подпрограмму вычисления определенного интеграла по формуле трапеций

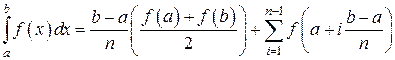
и, используя ее, вычислить

При расчетах n = 20.

14. Составить подпрограмму вычисления k-й степени квадратной матрицы из n х n элементов, используя подпрограмму умножения двух матриц. Найти А3, В4, где

15. Составить подпрограмму упорядочивания элементов одномерного массива по убыванию методом максимального элемента, используя подпрограмму нахождения номера максимального элемента последовательности чисел. Упорядочить по убыванию массивы:

X = (0.1; 0.5; 0.22; 0.05; 0.34; 0.99; 1.5);

У = (1.11; 1.33; 5.09; 4.95; 8.4).

16. Составить подпрограмму вычисления бесконечной суммы S с заданной точностью.

Используя подпрограмму, найти суммы:

17. Составить функцию определения косинуса угла между двумя векторами по формуле:

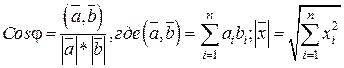
Для вычисления скалярного произведения и модуля использовать подпрограммы-функции. Найти косинусы углов между векторами с = (1; 2; 3); у = (1.1; 3.8; 4.1); z = (0.5; 0.1; 3.08).

18. Характеристикой строки матрицы назовем сумму положительных элементов этой строки. Составить подпрограмму, определяющую номер строки с максимальной характеристикой. Для вычисления характеристики использовать подпрограмму-функцию. Найти строки с максимальной характеристикой для матриц:

19. Характеристикой столбца прямоугольной матрицы размером m*n назовем максимальный элемент этого столбца. Составить подпрограмму определения минимальной характеристики в прямоугольной матрице. Для вычисления характеристики использовать подпрограмму. Найти минимальную характеристику для матриц А (размером 4x5) и В (размером 4x3). Исходные данные задать произвольно.

20. Характеристикой строки квадратной матрицы назовем среднее арифметическое значение элементов этой строки. Составить подпрограмму нахождения строки с минимальной и максимальной характеристиками. Для вычисления характеристики использовать подпрограмму-функцию. Поменять местами строки с максимальным и минимальным средним в квадратной матрице Z, из 25 элементов. Исходные данные задать произвольно.

21. Составить подпрограмму, которая присваивает элементам одномерного массива Z. значения функции f(х) в точках (x₁, x₂, ..., х_n). Сформировать одномерный массив А из значений функции f₁(х) = е^хсоs(х) в точках (0.1; 0.35; 0.37; 0.39; 0.45; 0.51) массив В из значений функции f₂(х) = 3sin(х) в течках (π/8; π /7; π /6; π /5; π /4).

22. Назовем характеристикой строки двумерного символьного массива число символов, относящихся к гласным русским буквам. Составить подпрограмму замены символов в строке с максимальной характеристикой на символ '*'. Произвести указанную замену символов для произвольных массивов размером (3*6) и (2*7).

Требования к отчёту по лабораторной работе:

1. оформить отчет по соответствующим требованиям (титульный лист)

2. сформулировать цель работы

3. задание;

4. схема алгоритм программы;

5. текст программы;

6. выводы по результатам выполнения лабораторной работы;

7. список используемой литературы (обязательно из электронной библиотеки).