Лабораторная работа № 6. Численное решение обыкновенных дифференциальных уравнений

Задание:Найти численное решение задачи Коши для данного дифференциального уравнения и начального условия 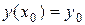на отрезке с шагом . Использовать метод, указанный преподавателем.

№ варианта	Уравнение	Начальное условие	a	b
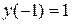
			-1	-0,1
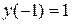
			-1	-0,1
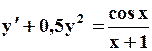
			1,6	2,6
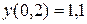
			0,2	1,2
		y(0)=0
		y(0)=0
		y(1)=2
		y(0)=0
		y(0)=0
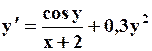
		y(0)=0
		y(1,2)=1	1,2	2,2
		y(0)=0
		y(1)=1
		y(0)=0
		y(1)=1
		y(0)=0
		y(2)=2
		y(0)=0
		y(0)=0
		y(1)=1
		y(0)=0
		y(0)=0
		y(2)=1
		y(0)=0
		y(0)=0
		y(1)=1
		y(0)=0
		y(1,5)=1	1,5	2,5
		y (0)=0,2
		y(0)=0,5
		y(0)=0
		y(1)=2
		y(0)=0
		y(0)=0,3
		y(0)=0,7

Вопросы для самоподготовки

1. Общая постановка задачи Коши.

2. Что является решением задачи Коши? Каков его геометрический смысл?

3. В чём состоит численное решение задачи Коши?

4. Метод Эйлера (алгоритм, геометрическая интерпретация, программа).

5. Метод Рунге-Кутта второго порядка (алгоритм, геометрическая интерпретация, программа).

6. Метод Эйлера-Коши (алгоритм, геометрическая интерпретация, программа).