
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ускорение
При прямолинейном движении быстрота изменения величины скорости  характеризуется ускорением а – изменением величины скорости за единицу времени.
характеризуется ускорением а – изменением величины скорости за единицу времени.
В случае произвольного криволинейного движения вектор скорости может меняться по величине и по направлению.
Быстрота изменения вектора скорости в этом случае характеризуется вектором ускорения  , расчленяемым на две составляющие, определяющие в отдельности быстроту изменения скорости по величине и быстроту изменения скорости по направлению.
, расчленяемым на две составляющие, определяющие в отдельности быстроту изменения скорости по величине и быстроту изменения скорости по направлению.
 |
На рисунке 3 изображен отрезок траектории между двумя соседними бесконечно близкими точками А и В. Скорости в этих точках
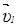 и
и  направлены по касательным к траектории в этих точках и отличаются по величине и по направлению.
направлены по касательным к траектории в этих точках и отличаются по величине и по направлению.
Рисунок 3
Причем рассматриваем случаи, когда скорость в точке В больше по величине. Перенесем вектор  параллельно самому себе в точку А. Соединяя конец вектора
параллельно самому себе в точку А. Соединяя конец вектора 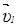 с концом вектора
с концом вектора  , получаем вектор
, получаем вектор  =
=  -
- 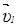 .
.
Это геометрическое приращение вектора  за время
за время  .
.
Тогда аср=  . Это отношение называется средним ускорением. Переходя к пределу, выражают мгновенное ускорение:
. Это отношение называется средним ускорением. Переходя к пределу, выражают мгновенное ускорение:
а =  =
=  . (7)
. (7)
Откладывая на перенесенном векторе  отрезок, численно равный длине вектора
отрезок, численно равный длине вектора 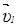 , видим, что вектор
, видим, что вектор  может быть представлен как геометрическая сумма двух векторов:
может быть представлен как геометрическая сумма двух векторов:
 =
=  -
-  , (8)
, (8)
где  - численно равен изменению величины скорости за
- численно равен изменению величины скорости за  :
:  =
=  -
- 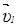 .
.
Если величина скорости не меняется, то  =0,
=0,  =0.
=0.
 характеризует изменение направления вектора скорости
характеризует изменение направления вектора скорости  за время
за время  . Он направлен в сторону вогнутости траектории. В выражение (7) поставим значение
. Он направлен в сторону вогнутости траектории. В выражение (7) поставим значение  из (8):
из (8):
 =
=  =
=  +
+ 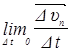 =
=  +
+  . (9)
. (9)
Вектор  =
=  также направлен по касательной к траектории, а модуль этого вектора равен аk =
также направлен по касательной к траектории, а модуль этого вектора равен аk =  - тангенциальное ускорение.
- тангенциальное ускорение.
Для определения второй составляющей в уравнении (9) восстановим перпендикуляры к касательным в точках А и В до пересечения их в точке О. Малая дуга  S = АВ есть отрезок окружности с центром в точке О и радиусом ОА=ОВ=R.
S = АВ есть отрезок окружности с центром в точке О и радиусом ОА=ОВ=R.
Треугольники АОВ и САD подобны, т.к. имеют одинаковые углы при вершине (углы со взаимно перпендикулярными сторонами).
Тогда  или
или  =
=  ,
, 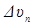 =
=  . Делим на
. Делим на  :
:  =
=  .
.
Переходя к пределу :
аn=  =
=  =
= 
 =
=  (10)
(10)
Таким образом, численное значение нормального ускорения в данной точке равно квадрату скорости, деленному на радиус кривизны в той же точке:
аn= 
Вектор ускорения есть векторная сумма нормального и тангенсального ускорения (уравнение 9).
 =
=  =
=  +
+ 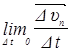 =
=  +
+  .
.
Дата добавления: 2015-02-10; просмотров: 139; Мы поможем в написании вашей работы!; Нарушение авторских прав |