СИТУАЦИОННОЕ МОДЕЛИРОВАНИЕ

В разд. 2.1 решение (4) уравнения измерения (2) полу­чилось приближенным из-за неточного знания поправки. Ситу­ации, в которых по какой-либо причине не хватает нужной количественной информации, часто встречаются в метроло­гии. Для математического описания таких ситуаций использу­ются ситуационные модели.

Предположим, например, что неизвестно значение Q не­которой физической величины Q. Требуется представить эту ситуацию математической моделью.

Если какие-либо значения Q более вероятны, чем другие, это должно быть принято во внимание. Тогда подбирается соответствующий закон распределения вероятности Q на ин­тервале возможных значений. Если же на этом интервале Q с одинаковой вероятностью может иметь любое значение, то закон распределения вероятности Q принимается равномерным. Выбранный закон распределения вероятности Q является математической моделью ситуации, состоящей в том, что зна­чение Q неизвестно. Эта модель не является стохастической, так как Q — неслучайное значение, и статистические законо­мерности здесь не проявляются. Чтобы подчеркнуть это, у си­туационных моделей величину, аналогичную дисперсии, обоз­начают через и²_Q.

На рис. 17 представлена графически математическая мо­дель ситуации, состоящей в том, что значение Q с одинако­вой вероятностью может быть любым на интервале от — Q_m до Q_m. Так как площадь, ограниченная осью абсцисс и графиком плотности распределения вероятности должна равняться единице, то

2Q_m p(Q) =1

Отсюда

р

Числовые характеристики этого "закона распределения ве­роятности" - среднего значения

что видно непосредственно из рисунка; аналог дисперсии

Вместо аналога дисперсии часто используется аналог сред­него квадратического отклонения

Пример 12. В рабочих условиях измерении температура на 1000 К превышает нормальную. Средством измерений является металличес­кая линейка из тугоплавкого сплава. Чему равна температурная поп­равка при измерениях длины в таких условиях?

Решение. Зависимость длины линейки от температуры имеет вид:

где l_H и t_H — длина линейки и температура, соответствующие нормаль­ным условиям, а a— коэффициент линейного расширения материала, из которого изготовлена линейка. Результат сравнения неизвестного значения L c l при t - t_H = 1000 К в (1 + 1000a) раз меньше результа­та сравнения L с l_H. Поэтому поправочный множитель (мультипликатив­ная температурная поправка)

c= 1 + 1000 a.

Коэффициент линейного расширения сплава a обыч­но неизвестен. По справоч­ным данным он может быть в пределах от 10^-6 К^-1 до 10^-5 К^-1. Отсут­ствие точных сведений об a можно учесть с помощью ситуационной модели, сог­ласно которой c с одина­ковой вероятностью может иметь любое значение в пределах интервала 0,001 c 1,01. Графическое изображение ситуационной модели дано на рис. 18, а. Числовые характеристики этого "закона распределения вероятности”

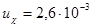
В рассматриваемом примере температурная по­правка может быть сконст­руирована и как аддитив­ная

u=1000aХ

Графическое изображение ситуационной модели в этом случае показано на рис. 18, б, а ее числовые характеристики равны:

Использование ситуационной модели является искусственным математическим приемом, позволяющем учесть дефицит информации о значении коэффициента линейного расширения а. Проведя соответствую­щие исследования и установив значение а, можно уточнить поправку, которая на самом деле является неслучайной и изображается точкой на числовой оси.

2.3.4. ОБНАРУЖЕНИЕ И ИСКЛЮЧЕНИЕ ОШИБОК

Надежность эргономической системы, в которую входят человек, окружающая среда, объект измерений и средство из­мерений, не безгранична. В ней могут происходить сбои, отка­зы аппаратуры, скачки напряжения в сети питания, сейсми­ческие сотрясения, отвлечение внимания оператора, описки в записях и многое другое, не имеющее отношения к измере­ниям. В результате появляются ошибки, вероятность кото­рых, как следует из теории надежности больших систем, не так уж мала.

При однократном измерении ошибка может быть обна­ружена только путем логического анализа или сопоставления результата с априорным представлением о нем. Установив и устранив причину ошибки, измерение можно повторить.

При многократном измерении одной и той же величины постоянного размера ошибки проявляются в том, что резуль­таты отдельных измерений заметно отличаются от осталь­ных. Иногда это отличие настолько большое, что ошибка очевидна. Остается понять и устранить ее причину или просто отбросить этот результат как заведомо неверный. Если отли­чие незначительное, то оно может быть следствием как ошибки, так и рассеяния отсчета, а, следовательно, показания и результата измерения, которые согласно основному посту­лату метрологии являются случайными. Нужно поэтому иметь какое-то правило, руководствуясь которым принимать реше­ния в сомнительных случаях.

После того, как все влияющие факторы учтены и все поп­равки в показания внесены, рассеяние результата измерения одной и той же физической величины постоянного размера нередко бывает следствием множества причин, вклад каж­дой из которых незначителен по сравнению с суммарным дей­ствием всех остальных. Центральная предельная теорема те­ории вероятности утверждает, что результат измерения при этом подчиняется так называемому нормальному закону, кри­вые плотности распределения вероятности которого

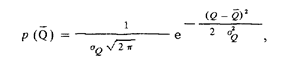
при различных значениях дисперсии показаны на рис. 9. Интег­ральная функция нормального закона распределения.

Если условия центральной предельной теоремы выполня­ются, то весь массив экспериментальных данных при много­кратном измерении одной и той же величины постоянного размера должен группироваться около среднего значения 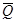, и выпадение какого-нибудь отдельного значения результата из­мерения из этого массива позволяет предположить, что он ошибочный. Найдем вероятность, с которой любое значение результата измерения, подчиняющегося нормальному закону распределения вероятности, должно находиться в пределах от Q₁ до Q₂:

Интегралы в этом выражении не могут быть выражены через элементарные функции. Более того, для интегральной функ­ции нормального закона распределения вероятности нет ни таблиц, ни графиков, так как с их помощью невозможно охватить все многообразие возможных значени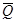й и . Произведем поэтому замену переменной:

Учитывая, что после такой замены d Q = d z, получим

Теперь интересующая нас вероятность выражена через раз­ность значений интегральной функции, соответствующей плот­ности распределения вероятности

характеризующей так называемый нормированный нормалъный закон. Дифференциальная и интегральная функции его показаны на рис. 19, а числовые характеристики

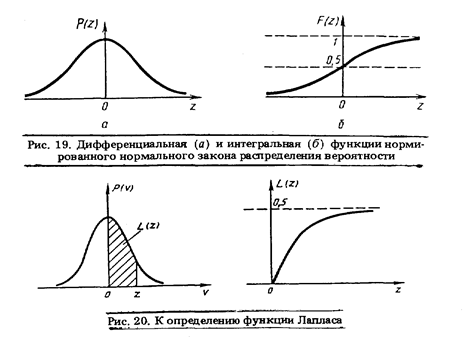
Из рис. 19, б видно, что

Эта функция, связанная с интегралом вероятности — функци­ей Лапласа (см. рис. 20)

табулирована в диапазоне значений z от 0 до 3,3, за предела­ми которого в сторону больших z практически неотличима от 1. Если выбрать z₂ = -z₁, и обозначить эту величину че­рез t, что будет соответствовать, как это показано на рис.21,

выбору границ интервала [Q₁;Q₂], равноотстоящих от соседнего значения Q на ± t 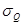, т.е.

то окончательно получим:

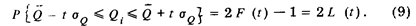
По табличным значениям функций, входящих в это урав­нение, построена верхняя кривая на рис. 22. Параметр t играет в метрологии важную роль. Он показывает, на сколько 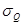cзаданной вероятностью может отличаться отдельное значение результата измерения, подчиняющегося нормальному закону распределения вероятности, от своего среднего значения. Так, например, из графика на рис. 22 видно, что

Эта вероятность называется доверительной, интервал [ - t ; + 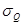] - доверительным интервалом, а его границы Q₁ и Q₂ - доверительными границами. Из графика следует, что доверительный интервал зависит от доверительной вероят­ности. С очень высокой вероятностью 0,997 все значения ре­зультата измерения, подчиняющегося нормальному закону, должны группироваться в пределах доверительного интер­вала Q ± 3 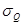. На этом основании можно сформулировать следующее правило: если при многократном измерении од­ной и той же физической величины постоянного размера сомнительное значение результата измерения отличается от среднего значения больше чем на 3 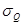, то с вероятностью 0,997 оно является ошибочным и его следует отбросить.Это правило называется "правилом трех сигм".

Пример 13. Одной из причин рассеяния результатов радиотехни­ческих измерений служит "шум" первых каскадов усиления в из­мерительных преобразователях. Напряжение "шума" является слу­чайной величиной, подчиняющейся нормальному закону распреде­ления вероятности с нулевым средним значением и дисперсией, рав­ной мощности "шума", выделяемой на сопротивлении 1 Ом.

Определить, не содержится ли ошибок в следующих эксперимен­тальных данных, полученных при измерении мгновенного значения шумового напряжения в отсутствии полезного сигнала: -4,2 мВ; 0,3 мВ; 5,7 мВ; -1,6мВ; -7,2мВ; 3,9 мВ; 2,2 мВ; -0,1 мВ; 1,4 мВ, если мощность "шума", выделяемая на нагрузке 1 Ом, равна 4 мкВт.

Решение. Среднее квадратическое отклонение мгновенного значе­ния шумового напряжения составляет 2 мВ

. По "правилу трех сигм", следовательно, нужно признать, что в пятом случае допущена какая-то ошибка.

Можно, конечно, принимать решения и с меньшей вероят­ностью. В рассмотренном примере с вероятностью 0,99, нап­ример, допущена ошибка и в третьем случае. На практике, од­нако, преимущественное распространение получило "правило трех сигм". Условием его применения служит уверенность в том, что результат измерения подчиняется нормальному за­кону распределения вероятности. Если такой уверенности нет, то указанное обстоятельство следует проверить. Так как ошибка искажает закон распределения вероятности результа­та измерения, то проверка его нормальности производится после исключения ошибки.Как это делается подробно рас­смотрено в разд. 2.6.2.

В некоторых случаях известно заранее, что результат из­мерения подчиняется равномерному закону распределения вероятности. Например, из-за люфтов и трения в опорах под­вижной части измерительного механизма он с равной вероят­ностью может отличаться от среднего значения на любую ве­личину в пределах общего люфта. Последний обычно извес­тен, так что появление больших отклонений может быть следствием только ошибок. Без дополнительной проверки они должны быть отброшены.

2.4. ИЗМЕРИТЕЛЬНАЯ ИНФОРМАЦИЯ

Измерение состоит в получении информации о значе­нии измеряемой величины. Означает ли это, что до измере­ния об этой величине ничего не известно?

Нет, не означает. Напротив, для того, чтобы провести измерение, нужно уже знать достаточно много. В первую оче­редь нужно хорошо себе представлять объект исследования. Внутренний диаметр полого шара не измерить ни обычной линейкой, ни микрометром. Для измерения расстояний меж­ду атомами в кристалле не годятся ни концевые, ни штрихо­вые меры длины. Некоторые измерительные задачи вообще бессмысленно ставить. Нельзя, например, измерить ни цвет, ни вкус, ни запах электрона. Нужно знатьразмерность изме­ряемой величины. В противном случае будет не ясно, с чем сравнивать ее размер: с метром? килограммом? секундой или другой единицей? Нужно иметь хотя бы ориентировочное представление и о ееразмере; температуру в доменной пе­чи не измерить уличным термометром; отсутствие представ­ления о силе электрического тока при грозовом разряде обер­нулось для Г.В. Рихмана трагедией. При постановке любых измерительных задач важно установить (а затем исключить, компенсировать, или как-то учесть)факторы, влияющие на результат измерения.

Информация, которой располагают до измерения, назы­вается априорной. Она всегда есть. Если об измеряемой ве­личине мы ничего не знаем, то ничего и не узнаем. С другой стороны, если об измеряемой величине известно все, то изме­рение не нужно. Необходимость измерения обусловлена де­фицитом информации о количественной характеристике из­меряемой величины.

Обязательное использование при измерении априорной информации можно рассматривать как второй постулат метрологии.

Наличие априорной информации о размере измеряемой величины выражается в том, что он не может быть любым в пределах от - до + . Всегда можно указать некоторые пределы, в которых находится значение измеряемой величи­ны, пусть даже очень грубо, сугубо ориентировочно. Если нельзя сказать, что в этих пределах какие-то значения изме­ряемой величины более вероятны, чем другие, то остается принять, что с одинаковой вероятностью измеряемая величина может иметь любое значение от Q₁ до Q₂, т.е. воспользовать­ся ситуационной моделью

представленной графически на рис. 23. Дефицит информации о количественной характеристике измеряемой величины

состоит в неопределенности ее значения на интервале [Q₁ ; Q₂]. Mepa этой неопределенности — энтропия

Таким образом, дефицит информации о значении измеря­емой величины перед измерением составляет

Рассмотрим теперь ситуацию, складывающуюся после выполнения измерения. Результат измерения является слу­чайным значением измеряемой величины. Если влияние пос­тоянно действующих и закономерно изменяющихся во вре­мени факторов компенсировано поправками, а ошибки исключены, то отдельные значения результата измерения являются либо завышенными, либо заниженными по чисто случайным причинам:

где случайное отклонение принимает значения, разные по абсолютной величине и знаку. Среднее значение случайного отклонения равно нулю. Поэтому

Таким образом, (см. рис. 24) значение измеряемой величи­ны равно среднему значению результата измерения. Несмещен­ность среднего значения результата измерения относительно значения измеряемой величины обеспечивает правильность измерения.

Однако на практике вычислить среднее значение резуль­тата измерения невозможно, так как при конечном объеме экспериментальных данных невозможно интегрирование в бесконечных пределах. Невозможно, следовательно, уста­новить и значение измеряемой величины. На практике исхо­дят из того, что никакое значение результата измерения с выбранной доверительной вероятностью не может отличать­ся от среднего значения больше, чем на половину довери­тельного интервала. Поэтому среднее значение результата из­мерения , а следовательно, и значение измеряемой величи­ны Q с такой же вероятностью не отличаются от любого зна­чения Q_i, больше, чем на половину доверительного интервала - рис. 25. Это позволяет после выполнения измерения уста­новить интервал [Q₃ ;Q₄] в котором с выбранной вероят­ностью находится значение Q.

Ничего определенного относительно того, чему равно Q в пределах установленного интервала, сказать нельзя. Можно поэтому принять, что на этом интервале любые зна­чения Q равновероятны, т.е. опять-таки воспользоваться ситуационной моделью

показанной на рис. 23. Всё значение измерения заключа­ется в том, что интервал [Q₃ ;Q₄] меньше интервала [Q₁ ;Q₂] в котором, как было установлено на основе анализа априорной информации, находится значение изме­ряемой величины. Таким образом, можно сказать, что измерение состоит в уточнении значения измеряемой ве­личины. Однако точное значение остается неизвестным и после измерения. Остаточная неопределенность составляет

то есть после измерения дефицит информации о значении измеряемой величины уменьшается на

Эта величина интерпретируется как количество информа­ции, получаемой в результате измерения, а протяженность интервалов [Q₁ ;Q₂] и [Q₃ ;Q₄] характеризует точность, с которой известно значение физической величины до и после ее измерения.

По ширине доверительного интервала, в котором с выбранной доверительной вероятностью устанавливается значение измеряемой величины, измерения делятся на из­мерения низкой, высокой, высшей и наивысшей точнос­ти (см. рис. 26). Технические средства, обеспечивающие высший и наивысший уровни точности, для практических измерений не используются. Подробно они рассматрива­ются в разд. 3. Средства измерений могут быть высокой и низкой точности, хотя такая градация весьма условна: отдельные уникальные средства измерений могут достигать наивысшего уровня точности. Кроме того, нужно иметь ввиду, что точность измерений определяется не только точностью средств измерений, но и многими другими факторами, рассмотренными в разд. 2.3. Предельно дости­жимой точности измерений посвящена гл. 8.