
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Сравнение двух генеральных средних
Рассмотрим две независимые выборки x1,x2,...,xnи y1,y2,...,yn, извлеченные из нормальных генеральных совокупностей с одинаковыми дисперсиями 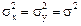 , причем объемы выборок соответственно n и m, а средние
, причем объемы выборок соответственно n и m, а средние 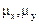 и дисперсия
и дисперсия 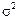 неизвестны. Требуется проверить гипотезу о том, что
неизвестны. Требуется проверить гипотезу о том, что  . Альтернативной является гипотеза
. Альтернативной является гипотеза 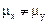 .
.
Как известно, выборочные средние – нормально (или приблизительно - нормально) распреде-ленные величины, следовательно, их разность 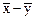 – нормальная величина со средним
– нормальная величина со средним 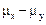 и дисперсией, которая вычисляется по формуле:
и дисперсией, которая вычисляется по формуле:
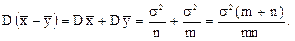
Если бы дисперсия 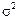 была известна, мы могли бы для проверки гипотезы воспользоваться свойствами и таблицами нормального распределения, как мы это делали при построении довери-тельного интервала для среднего при известной дисперсии. В силу того, что
была известна, мы могли бы для проверки гипотезы воспользоваться свойствами и таблицами нормального распределения, как мы это делали при построении довери-тельного интервала для среднего при известной дисперсии. В силу того, что 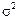 неизвестна, заменим в наших рассуждениях неизвестную дисперсию на ее эмпирический аналог.
неизвестна, заменим в наших рассуждениях неизвестную дисперсию на ее эмпирический аналог.
Итак, для проверки гипотезы  построим статистику:
построим статистику:
 ,
,
где
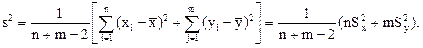
Теперь к статистике t применим те же рассуждения, которые мы применяли к статистике Т.
Если гипотеза  верна, статистика t имеет распределение Стьюдента с n+m–2 степенями свободы и в качестве области Ibможно взять интервал, симметричный относительно 0, в который величина x, распределенная по Стьюденту, попадает с вероятностью b, т.е.
верна, статистика t имеет распределение Стьюдента с n+m–2 степенями свободы и в качестве области Ibможно взять интервал, симметричный относительно 0, в который величина x, распределенная по Стьюденту, попадает с вероятностью b, т.е.
Ib= [–tn+m–2;b+tn+m–2;b], где P(|x| < tn+m–2;b) = b.
Таким образом, если нам заданы две выборки и уровень значимости a, мы вычисляем значение статистики t и ищем по a, n и m в таблице 6 (в ней содержатся критические значения распределения Стьюдента) значение tn+m–2;a. Если выполняется

то мы принимаем гипотезу о том что  . И отвергаем гипотезу
. И отвергаем гипотезу  , если это неравенство не выполняется, так как произошло событие из дополнительной области, вероятность которой a. На рисунке 4.1 заштрихованная площадь (вероятность попасть в область) равна
, если это неравенство не выполняется, так как произошло событие из дополнительной области, вероятность которой a. На рисунке 4.1 заштрихованная площадь (вероятность попасть в область) равна
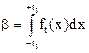 ,
,
на рисунке 4.2 заштрихована площадь a = 1–b области, где гипотеза не принимается.
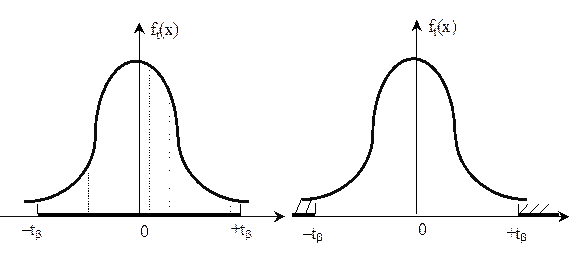
Рисунок 4.1 Рисунок 4.2
Если оказалось, что  , можно проверять гипотезу о том, что
, можно проверять гипотезу о том, что  , когда альтернативной гипотезой является
, когда альтернативной гипотезой является 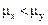 .В этом случае строится “односторонняя” область, попадание в которую дает основание принять основную гипотезу. А именно, в таблице 6 в нижней строке отыскивается a = 1 – b, где b – заданный уровень доверия, в строке с нужным числом степеней свободы находим границу интервала tn+m–2;a. Далее, если выполняется:
.В этом случае строится “односторонняя” область, попадание в которую дает основание принять основную гипотезу. А именно, в таблице 6 в нижней строке отыскивается a = 1 – b, где b – заданный уровень доверия, в строке с нужным числом степеней свободы находим границу интервала tn+m–2;a. Далее, если выполняется:

то первая гипотеза неверна и принимается, что 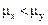 .
.
Можно проверять гипотезу о том, что  , когда альтернативной гипотезой является
, когда альтернативной гипотезой является 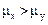 . В этом случае также строится “односторонняя” область, попадание в которую дает основание принять первую гипотезу (рисунок 4.3). А именно, гипотеза о том, что
. В этом случае также строится “односторонняя” область, попадание в которую дает основание принять первую гипотезу (рисунок 4.3). А именно, гипотеза о том, что 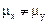 не принимается, а принимается гипотеза тогда, когда
не принимается, а принимается гипотеза тогда, когда
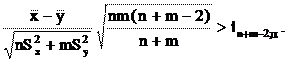
C помощью нижней строки таблица 6 распределения Стьюдента (см. приложение 3) мы решали уравнения:
P{d < –tn+m–2;a} = a, и P{d > tn+m–2;a} = a,
где a – уровень значимости.

Рисунок 4.3
Замечание.Было бы корректно сначала проверить гипотезу о равенстве дисперсий с помощью их выборочных оценок. Во второй части нашего руководства мы научимся делать такую проверку. Использовать значение статистики Т можно только, если прошла гипотеза о равенстве дисперсий. Если дисперсии 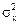 и
и 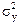 неизвестны и не предполагается, что они равны, статистика Т также имеет распределение Стьюдента. Но соответствующее ему число степеней свободы опреде-ляется приближенно и более сложным образом.
неизвестны и не предполагается, что они равны, статистика Т также имеет распределение Стьюдента. Но соответствующее ему число степеней свободы опреде-ляется приближенно и более сложным образом.
Итак, перечислим критерии, по которым проверяется статистическая гипотеза о том, что средние значения двух генеральных совокупностей, имеющих одинаковые дисперсии, совпадают (mx= my) на уровне значимости a. Они выведены из формул для двустороннего и одностороннего доверительного интервала для уровня доверия b = 1–a.
Вычисляем по выборке значение статистики t:
 ,
,
где
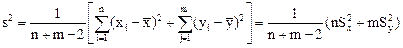 .
.
1. Критическая область для односторонней проверки гипотезы, что средние значения двух генеральных совокупностей совпадают (  ) по сравнению с альтернативой
) по сравнению с альтернативой 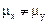 на уровне значимости a определяется неравенством:
на уровне значимости a определяется неравенством:
|t| > tn–1;a
(tn–1;aотыскивается по таблице 6 критических значений распределения Стьюдента, a в нижней строке).
2. Критическая область для односторонней проверки гипотезы, что средние значения двух генеральных совокупностей совпадают (  ) по сравнению с альтернативой
) по сравнению с альтернативой 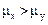 на уровне значимости a определяется неравенством:
на уровне значимости a определяется неравенством:
t > tn–1;a
(tn–1;aотыскивается по таблице 6 критических значений распределения Стьюдента, a в нижней строке).
Если вычисленное значение статистики t попадает в критическую область, то основная гипотеза отвергается. Вероятность попадания в эту область равна принятому уровню значимости a. В этом случае принимается альтернативная гипотеза.
Пример 4.2. Результаты исследования двух сортов резины на покрышках (в баллах) приведены в таблице:
| Номер покрышки | ||||
| Износ для сорта А | ||||
| Износ для сорта В |
Сделать проверку гипотезы о том, что резина сорта А больше изнашивается, чем резина сорта В.
Дата добавления: 2015-04-11; просмотров: 121; Мы поможем в написании вашей работы!; Нарушение авторских прав |