
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение.
 ,
,
 .
.
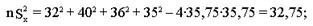

 .
.
Статистика распределена по Стьюденту с шестью степенями свободы. Значение t = 5,2 вы-ходит далеко за пределы интервала, имеющего уровень доверия 0,99 (этот интервал (–3,14; 3,14)). Следовательно, гипотеза о том, что оба сорта резины изнашиваются одинаково, не проходит. А проходит альтернативная ей “односторонняя” гипотеза о том, что резина сорта А изнашивается сильнее.
Заметим, что сделанный вывод “заметен на глаз” и без расчетов. Такой результат получится во всех случаях, когда вычисленное по испытаниям значение статистики t > 4. При близости значения t к числам 2 или 3 вывод может включать в себя уровень доверия к нему как параметр (вспомните правила двух и трех s). Если уровень доверия, с которым сделан вывод, не устраивает, надо позаботиться об улучшении опыта, например, увеличить число испытаний. Покажем это на примере.
Пример 4.3. Сравниваются две марки бензина А и В. На 11 машинах одинаковой мощности при разовом пробеге по кольцевому шоссе испытан бензин марок А и В. При испытании бензина марки В одна машина в пути вышла из строя и для нее данные по бензину отсутствуют. Расход бензина в пересчете на 100 км пути задан таблицей:
| I | ||||||||||||
| xi | 10,51 | 11,86 | 10,5 | 9,1 | 9,21 | 10,74 | 10,75 | 10,8 | 11,3 | 11,8 | 10,9 | N=11 |
| yi | 13,23 | 13,0 | 11,5 | 10,4 | 11,8 | 11,6 | 10,64 | 12,3 | 11,1 | 11,6 | – | m=10 |
Дисперсия расхода марок бензина А и В неизвестна и предполагается одинаковой. Можно ли с уровнем доверия 0,95 принять, что истинные средние расходы этих видов бензина одинаковы?
1. Вычисляем по выборкам:
 ,
, 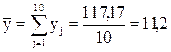 ,
,
 ,
,
 .
.
2. Находим из таблицы 6 критических значений распределения Стьюдента t19;0,95= 2,1.
3. Так как |t| < t19;0,95не выполняется, гипотезу о том, что средние значения норм расхода бензина марок А и В на 100 км пути совпадают, принять не можем, расхождение между  и
и  не объясняется только естественным разбросом данных.
не объясняется только естественным разбросом данных.
4. Заметим, что если бы разброс Q оказался бы много больше, например, вдвое, то знамена-тель увеличился в 1,41 раза и изменился бы и наш вывод – при таком большом разбросе расхож-дение между эмпирическими средними уже объяснялось бы естественным разбросом данных, а не расхождением теоретических средних.
5. Проверяем гипотезу о том, что 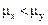 . С помощью нижней строки таблицы 6 распреде-ления Стьюдента решаем уравнение:
. С помощью нижней строки таблицы 6 распреде-ления Стьюдента решаем уравнение:

Так как –2,7 < –1,8, то гипотеза 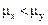 с уровнем доверия 0,95 может быть принята.
с уровнем доверия 0,95 может быть принята.
По таблице видно, что эта гипотеза заслуживает доверия, которое можно оценить даже выше – в 99 %.
Вывод.Средний расход бензина на 100 км для марки В больше, чем для марки А, с уровнем доверия 99 %.
Дата добавления: 2015-04-11; просмотров: 114; Мы поможем в написании вашей работы!; Нарушение авторских прав |