Число оборотов в единицу времени есть величина, обратная периоду. Она называется частотой вращения

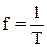.(3)

Нетрудно получить связь между угловой и линейной скоростью точки.

При движении по окружности элемент дуги связан с бесконечно малым поворотом соотношением . Отсюда .

Подставив его в (1), находим, что модуль линейной скорости будет равен

. (4)

Формула (4) связывает величины угловой и линейной скоростей.

Более общее соотношение очевидно из чертежа, где вектор линейной скорости представляет собой векторное произведение вектора угловой скорости – и радиуса-вектора точки :

. (5)

Справочный материал.

1. Векторным произведениемвекторов и называется вектор , величина которого равна площади параллелограмма, построенного на векторах сомножителях, а собственно векторы , и образуют правую тройку векторов.

2. Векторы { , , } образуют правую тройку, если кратчайший поворот от вектора к вектору , видимый из конечной точки вектора , может быть произведен в направлении «против часовой стрелки».

//Фильм «Векторная математика в физике»_6 мин.//

Определение 5.

Угловое ускорение — это производная по времени от вектора угловой скорости (соответственно вторая производная по времени от угла поворота)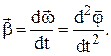

3. Примеры расчёта кинематических характеристик автомобиля.

Пример №1.

Гоночный автомобиль движется на прямолинейном участке траектории так, что его ускорение растёт линейно и за первые 10с достигает значения 5 м/с². Пренебрегая его собственными размерами и массой, определить в конце 10-ой секунды: 1) скорость автомобиля; 2) пройденный им путь.

Решение.

Поскольку ускорение растёт линейно, то 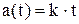и неизвестный коэффициент пропорциональности – 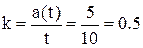м/с.

По условию движение – прямолинейно, следовательно, скорость –

м/с. (1)

Пройденный путь прямолинейного движения будет равен:

м. (2)

Ответы:

1) по формуле (1) – м/с; 2) по формуле (2) – м.

Пример №2.

Трековая модель автомобиля вращается на привязи с частотой 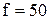Гц. После прекращения тяги, модель, сделав оборотов, остановилась. Пренебрегая собственными размерами и массой модели автомобиля, определить угловое её ускорение – 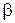, если считать, что торможение является равнозамедленным.

Решение.

Поскольку торможение принимается равнозамедленным, то угол поворота –

(1),

где угловая частота вращения, Гц (2).

Конечное значение угла – 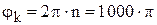рад (3).

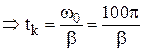Конечное значение угловой частоты вращения – , следовательно из соотношения – , где момент остановки с (4).

Подставляя в выражение (1) соотношения (2), (3), (4), находим, что рад/c.

Примечание.Решение можно получить в общем виде, полагая, что 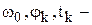определены общими выражениями – (2÷4). Тогда рад/c.