Ускорение точек плоской фигуры.

Теорема 4 (об ускорении точек плоской фигуры). Ускорение любой точки плоской фигуры равно векторной сумме ускорения полюса и ускорения за счет вращения фигуры вокруг полюса (оси, проходящей через полюс перпендикулярно плоскости фигуры).

.

Продифференцируем выражение (22) по времени, получим доказательство теоремы (рис. 31):

. (26)

Изменение вращательной вокруг полюса (оси, проходящей через полюс перпендикулярно плоскости фигуры) скорости _BA по времени характеризуется ускорением 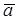_BA, имеющим две составляющих: вращательное ускорение и осестремительное ускорение (Р).

Рис. 31.

Из выражений (20) и (21) следует, что:

, (рис. 31);

, (рис. 31).

Причем вектор осестремительное ускорение направлен к полюсу (точке A).

Значит, ускорение за счет вращения фигуры S вокруг полюса 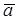_BA определяется следующим образом (рис. 31):

, . (27)