Ускорение точек тела при свободном движении.

Рис. 45.

Ускорение 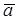_M любой точки M тела, движущегося свободно, равно (рис. 45) векторной сумме ускорения 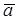_O точки O, вместе с которой тело движется поступательно, и ускорения 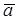_MO сферического движения тела вокруг этой точки:

.

Ускорение 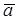_MO определяется формулой Ривальса и равно векторной сумме двух составляющих: вращательного ускорения и осестремительного ускорения:

. (33)

Вращательное ускорениеточки M равно векторному произведению вектора углового ускорения тела на радиус-вектор , соединяющий точку тела O с точкой M (20):

. (34)

Осестремительное ускорениеточки M равно векторному произведению вектора угловой скорости 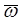тела на вектор вращательной скорости точки M (21):

. (35)

Сложное движение точки.

Основные понятия сложного движения точки.

Если точка M участвует в двух или более движениях, то такое её движение называется сложным движением.

Примером сложного движения точки M является её движение по телу D, движущемуся относительно неподвижной прямоугольной декартовой системы координат Ox₁y₁z₁ (рис. 46). Другую систему координат Oxyz скрепим с телом D. Точка M движется по телу D относительно подвижной системы координат Oxyz.

Рис. 46.

Движение точки M относительно неподвижной системы координат называется абсолютным и определяется радиус-вектором , начало которого совпадает с точкой O₁, а конец – с точкой M (рис. 46). Скорость точки M относительно неподвижной системы координат называется абсолютной скоростью и обозначается . Абсолютное ускорение характеризует изменение абсолютной скорости точки M в её абсолютном движении.

Движение точки M относительно подвижной системы координат Oxyz, связанной с движущимся телом D, называется относительным и определяется радиус-вектором , начало которого совпадает с точкой O, а конец – с точкой M (рис. 46). Скорость точки M относительно подвижной системы координат (тела D) называется относительной скоростью и обозначается . Относительное ускорение характеризует изменение относительной скорости точки M в её относительном движении.

Пусть положение осей подвижной системы координат Oxyz определяют орты , и (рис. 46). Зная координаты x, y, z точки M в этой системе координат, можно введенные характеристики определить выражениями:

, , ,

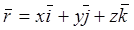где , , и , , .

Движение точки M вместе с подвижной системой координат, связанной с движущимся телом D, называется переносным. Скорость той точки тела D, с которой в данный момент совпадает движущаяся по телу точка M, называется переносной скоростью точки M и обозначается . Ускорение той точки тела D, с которой в данный момент совпадает движущаяся по телу точка M, называется переносным ускорением точки M и обозначается .