Цепь с последовательным соединением элементов

Проведем анализ работы электрической цепи с последовательным соединением элементов R, L, С.

Положим, что в этой задаче заданы величины R, L, С, частота f, напряжение U. Требуется определить ток в цепи и напряжение на элементах цепи. Из свойства последовательного соединения следует, что ток во всех элементах цепи одинаковый. Задача разбивается на ряд этапов.

1. Определение сопротивлений.

Реактивные сопротивления элементов L и С находим по формулам

X_L = ωL, X_C = 1 / ωC, ω = 2πf.

Полное сопротивление цепи равно

,

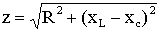угол сдвига фаз равен

(2.42)

φ = arctg((X_L - X_C) / R),

2. Нахождение тока. Ток в цепи находится по закону Ома

I = U / Z, ψ_i = ψ_u + φ.

Фазы тока и напряжения отличаются на угол φ.

3. Расчет напряжений на элементах. Напряжения на элементах определяются по формулам

U_R = I R, ψ_uR = ψ_i ;

U_L = I X_L, ψ_uL = ψ_i + 90° ;

U_C = I X_C, ψ_uC = ψ_i - 90°.

Для напряжений выполняется второй закон Кирхгофа в векторной форме.

Ú = Ú_R + Ú_L + Ú_C.

4. Анализ расчетных данных. В зависимости от величин L и С в формуле (2.42) возможны следующие варианты: X_L > X_C; X_L < X_C; X_L = X_C.

Для варианта X_L > X_C угол φ > 0, U_L > U_C. Ток отстает от напряжения на угол φ. Цепь имеет активно-индуктивный характер. Векторная диаграмма напряжений имеет вид (рис. 2.16).

Для варианта X_L < X_C угол φ < 0, U_L < U_C. Ток опережает напряжение на угол φ. Цепь имеет активно-емкостный характер. Векторная диаграмма напряжений имеет вид (рис. 2.17).

Для варианта X_L = X_C угол φ = 0, U_L = U_C. Ток совпадает с напряжением. Цепь имеет активный характер. Полное сопротивление z=R наименьшее из всех возможных значений X_L и X_C. Векторная диаграмма напряжений имеет вид (рис. 2.18).

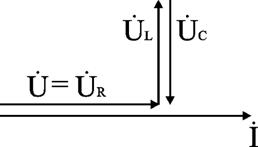
Этот режим называется резонанс напряжений (U_L = U_C). Напряжения на элементах U_L и U_C могут значительно превышать входное напряжение.

Пример.

U = 220 B, f = 50 Гц, R = 22 Ом, L = 350 мГн, С = 28,9 мкФ.

X_L = ωL = 2πf L = 2 · 3,14 · 50 · 0,35 = 110 Ом;
X_C = 1 / ωC = 1 / (2πf C) = 110 Ом;
Z = R = 22 Ом, φ=0, I = U / R = 220 / 22 = 10 А, ψ_u = ψ_i;
U_L = U_C = I X_L = 10 · 110 = 1100 В.

В приведенном примере U_L и U_С превышают входное напряжение в 5 раз.