Символический метод расчета

Если в установившемся режиме функция источника энергии имеет гармонический вид, то напряжения на линейных элементах цепи и токи ветвей также будут изменяться по гармоническому закону. Рассмотрим, как изменяются токи и напряжения для резистора, катушки индуктивности и конденсатора по рис. 4.7.

Уравнения по второму закону Кирхгофа для схемы рис. 4.7, а:

(4.7)

и по первому закону Кирхгофа для схемы рис. 4.7, б:

(4.8)

а	б
Рис. 4.7. RLС-цепи

Для гармонических функций выражения (4.7) и (4.8) имеют вид:

Для анализа и расчета полученных уравнений удобно использовать символический метод. Суть его состоит в представлении гармонических функций комплексными величинами. При этом уравнения, составленные для фиксированной частоты в интегрально-диф-ференциальной форме, переходят в алгебраические уравнения с комплексными величинами токов, напряжений и ЭДС. Каждой гармонической функции а(t) можно поставить в соответствие комплексное число называемое комплексной амплитудой (комплексом) гармонической функции (рис. 4.8)

(4.11)

Рис. 4.8. Векторное представление гармонической функции

Модуль равен амплитуде гармонической функции а аргумент 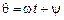ее фазе. Мнимая часть комплексной величины равна исходной гармонической функции:

. (4.12)

Обозначим А_m ∙ e^jψ= – комплекс амплитудного значения.

Преобразуя (4.7) и (4.8) с учетом (4.9), (4.10) и (4.12), получим:

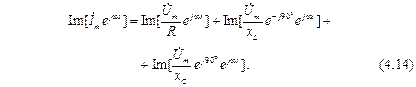
где – комплексная амплитуда ЭДС;

– комплексная амплитуда тока;

– комплексная амплитуда напряжения;

– вектор вращения.

Соотношения (4.13) и (4.14) можно упростить, учитывая и используя свойства комплексных функций и сократив подобные члены. В результате получим законы Кирхгофа в комплексной форме для амплитудных значений для схем рис. 4.7:

(4.15)

(4.16)

Законы Кирхгофа в комплексной форме для действующих значений токов и напряжений имеют вид:

(4.17)

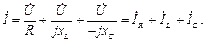(4.18)

Законы Кирхгофа в комплексной форме:

1. Алгебраическая суммакомплексных значений токов в проводниках, соединенных в узел, равна нулю:

 

 

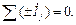
2. Алгебраическая сумма всех комплексных источников ЭДС в любом замкнутом контуре цепи равна алгебраической сумме комплексных падений напряжений на всех остальных элементах того же контура:

 

 

Для иллюстрации взаимосвязи между токами и напряжениями в конкретной схеме строят векторные диаграммы: для напряжений – топографические, построенные с соблюдением порядка расположения элементов в цепи, для токов – лучевые, построенные для выбранных узлов схемы, причем вектора выходят из начала координат или какой-то другой выбранной точки. Векторные диаграммы изображают законы Кирхгофа в комплексной форме, представленные суммой векторов на комплексной плоскости.

На рис. 4.9 показаны векторные диаграммы (топографическая для напряжений и лучевая диаграмма для токов), построенные по уравнениям (4.17) и (4.18) для схем рис. 4.7. При построении диаграмы выбираются удобные для анализа масштабы напряжений и токов, при этом длина векторов напряжений и токов будет пропорциональна их действующим значениям, а угол поворота векторов относительно вещественной оси равен их начальной фазе. Положительные значения углов отсчитываются против направления вращения часовой стрелки, а отрицательные – по часовой стрелке.

 

а	б
Рис. 4.9. Векторные диаграммы токов и напряжений

 

Уравнения (4.17) и (4.18) позволяют определить токи в ветвях и напряжения на элементах цепи. Так, для схемы рис. 4.7, а:

 

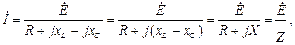(4.19)

 

где X – суммарное реактивное сопротивление ветви;

– комплексное сопротивление ветви;

Z и j – модуль и аргумент комплексного сопротивления.

Для схемы рис 4.7, б из (4.18):

 

(4.20)

 

где g и b – активная и реактивная проводимости параллельных ветвей;

– суммарная комплексная проводимость цепи;

Y и y – модуль и аргумент комплексной проводимости.

Сопротивления Z, R и X, а также проводимости Y, g и b образуют треугольники сопротивлений и проводимостей (рис. 4.10).

а	б
Рис. 4.10. Треугольники сопротивлений и проводимостей