
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Электроснабжение
Назначение и основные типы электрических станций. Электростанции на основе возобновляемых источников энергии: Солнца, воды, ветра, растительных и биологических видов топлива. Передвижные и резервные электростанции.
Назначение, основные типы и электрооборудование электрических подстанций. Основные схемы и особенности электроэнергоснабжения сельскохозяйственных потребителей.
Электрические нагрузки. Линии электропередачи воздушные и кабельные.
Государственная политика электроэнергосбережения при производстве, передаче, распределении и применении электрической энергии. Виды основных потерь электрической энергии и способы их снижения. Показатели качества электроэнергии и их влияние на работу однофазных и трехфазных электроприемников. Основные правила безопасной эксплуатации стационарных и передвижных электроустановок в сельском хозяйстве.
Варианты задач и методические указания
по выполнению контрольноГО ЗАДАНИЯ
Учебным планом для студентов-заочников по курсу «Электротехника и электроника» предусмотрено выполнение одного контрольного задания. Задание предусматривает решение пяти контрольных задач. Кроме того, каждое контрольное задание разбито на варианты.
Студенты-заочники должны готовить решение контрольного задания по своему варианту. Номер принципиальной электрической схемы выбирается по предпоследней цифре шифра студента, по последней цифре шифра выбирается номер варианта.
При выполнении контрольного задания необходимо соблюдать следующие правила:
1. Выполнение каждой задачи должно сопровождаться краткими объяснениями, необходимыми обоснованиями и подробными вычислениями;
2. Задачу следует решить сначала в общем виде (формулы в буквенных выражениях), и только затем, после необходимых преобразований, подставлять соответствующие числовые значения;
3. При вычислении каждого значения нужно пояснить словами, какая величина определяется;
4. Размерность всех заданных в условиях задач величин и полученных результатов необходимо указать в соответствии с системой СИ;
5. Электрические схемы должны быть вычерчены согласно установленным правилам (ГОСТ 2.702-75; 2.705-70; 2.722-68; 2.723-74; 2.728-74; 2.730-73; 2.710-81 «Обозначения буквенно-цифровые в электрических схемах»);
6. Графический материал желательно выполнять на миллиметровой бумаге;
7. Задача должна быть написана разборчивым почерком с ясным изображением букв и цифр текста, формул и числовых выкладок.
Чтобы получить полное представление по рассматриваемому вопросу, перед выполнением контрольного задания студент должен изучить соответствующую литературу, а также решить упражнения и задачи, приведенные в учебниках. Основные моменты решения задач, в дополнение к рекомендуемой литературе, приводятся ниже в методических рекомендациях.
Задача 1
В сеть с переменным синусоидальным напряжением U и током I включены последовательно резисторы, индуктивные катушки и конденсаторы (рис.1). Данные для расчета заданы в табл.1, в которой указаны значения напряжения или тока, активные сопротивления, индуктивности и емкости, частота питающего напряжения.
Требуется определить:
1. Показания измерительных приборов, включенных в цепь: амперметра, вольтметра, ваттметра и фазометра.
2. Построить векторную диаграмму напряжений.
3. Для принципиальных электрических схем № 1, 3, 5 определить собственную частоту колебаний fo.
4. Для принципиальной электрической схемы № 1 определить значение ёмкости С при которой в цепи наступит резонанс напряжений.
5. Для принципиальной электрической схемы №4 определить значение индуктивности L, при которой в цепи наступит резонанс напряжений.
Методические рекомендации по решению задачи 1.
Первая задача относится к расчету однофазной цепи переменного синусоидального тока с последовательным соединением резисторов Ri, индуктивных катушек XLj и конденсаторов ХCК. Для решения задачи необходимо изучить § 5.7., § 5.8., § 5.5 из [1] или § 3.10, § 3.11 из [2], с. 65...68.
В условии задачи даны численные значения активных сопротивлений R в омах (Ом), индуктивностей катушек L в милигенри (мГн), ёмкостей конденсаторов С в микрофарадах (мкФ), частота напряжения или тока f в герцах (Гц), входное напряжение U в вольтах (В) или входной ток I в амперах (А), табл. 1.
Сопротивление индуктивной катушки XL определяется по формуле:
XL = wL = 2pfL, (1)
где w - угловая частота, рад/с;
f - промышленная частота, Гц;
L - индуктивность катушки, Гн.
Сопротивление конденсатора:
 (2)
(2)
где С - ёмкость конденсатора, Ф.
Рис 1. Принципиальные электрические схемы к задаче 1.
Таблица 1 – Исходные данные к задаче 1
| Варианты | Данные для расчёта | ||||||||
| Предпоследняя цифра шифра | Последняя цифра шифра | U | I | f | R1 | R2 | L | C1 | C2 |
| В | А | Гц | Ом | Ом | мГн | мкФ | мкФ | ||
| 0…1 схема №1 | 0...1 | - | - | ||||||
| 2…3 | - | - | |||||||
| 4…5 | - | - | |||||||
| 6…7 | - | - | |||||||
| 8…9 | - | - | |||||||
| 2…3 схема №2 | 0...1 | - | 0,2 | - | - | ||||
| 2…3 | - | 0,4 | - | - | |||||
| 4…5 | - | 0,6 | - | - | |||||
| 6…7 | - | 0,8 | - | - | |||||
| 8…9 | - | 1,0 | - | - | |||||
| 4…5 схема №3 | 0...1 | - | |||||||
| 2…3 | - | ||||||||
| 4…5 | - | ||||||||
| 6…7 | - | ||||||||
| 8…9 | - | ||||||||
| 6…7 схема №4 | 0...1 | - | - | ||||||
| 2…3 | - | - | |||||||
| 4…5 | - | - | |||||||
| 6…7 | - | - | |||||||
| 8…9 | - | - | |||||||
| 8…9 схема №5 | 0...1 | - | - | ||||||
| 2…3 | - | - | |||||||
| 4…5 | - | - | |||||||
| 6…7 | - | - | |||||||
| 8…9 | - | - |
Примечание. Чтобы получить значения реактивных сопротивлений в Омах, необходимо в соответствующие формулы подставлять значения индуктивностей и емкостей соответственно в генри (Гн) и фарадах (Ф) (1мГн = 10-3 Гн , 1мкФ = 10-6 Ф).
Полное сопротивление Z последовательной цепи вычисляется по формуле:
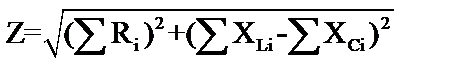 , (3)
, (3)
где S- оператор, означающий суммирование;
i - порядковый номер элемента.
Сила тока в цепи определяется по заданному напряжению U и полному сопротивлению Z по закону Ома:
 . (4)
. (4)
Входное напряжение определяется по соответствующей формуле:
 . (5)
. (5)
Активная мощность цепи в ваттах (Вт) или в киловаттах (кВт) вычисляется по формуле:
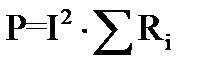 . (6)
. (6)
Индуктивная мощность цепи в варах (вар) или в киловарах (квар) вычисляется по формуле:
 . (7)
. (7)
Ёмкостная мощность цепи также в варах или киловарах вычисляется по формуле:
 . (8)
. (8)
Полная мощность цепи в вольтамперах (ВА) или в киловольтам-перах (кВА):
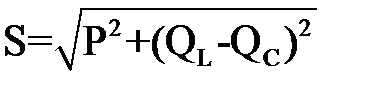 . (9)
. (9)
Показание ваттметра численно равно значению активной мощности из формулы (6), а показание фазометра определяется по формуле
 . (10)
. (10)
где RК - активное сопротивление участка цепи к которому подключена катушка напряжения фазометра;
ZК - полное сопротивление данного участка.
Показание вольтметра, вычисляется по формуле (5), в которой сопротивление Z заменяется сопротивлением ZК участка цепи, к которому подключен вольтметр.
Показание амперметра численно равно значению тока I из формулы (4).
Собственная частота колебаний fO вычисляется по формуле:
 . (11)
. (11)
где L - общая индуктивность цепи, Гн;
С - общая ёмкость цепи, Ф.
Формулы для вычисления L и C:
L = L1 + L2 + … + Li; (12)
 . (13)
. (13)
Значения резонансной ёмкости или индуктивности определяется из условия резонанса напряжений для последовательной цепи:
 . (14)
. (14)
Векторную диаграмму напряжений цепи нужно строить следующим образом:
1) записать векторное уравнение напряжений на основании 2-го закона Кирхгофа:
 . (15)
. (15)
2) выбрать базовый вектор, относительно которого строят векторную диаграмму напряжений. В последовательной цепи это, как правило, вектор тока Ī;
3) учитывать, что векторы ŪRi совпадают по фазе с вектором тока Ī; векторы ŪLi опережают вектор Ī на 900; векторы ŪCi отстают от вектора Ī на 900. Кроме того, иметь в виду, что векторные слагаемые формулы (15) подчиняются законам переместительности и сочетательности.
Задача 2
В сеть с переменным синусоидальным напряжением U и током I, частотой f = 50 Гц включены последовательно-параллельно резисторы, индуктивные катушки и конденсаторы (рис.2). Данные для расчета параллельной цепи заданы в табл. 2, в которой указаны значения напряжения или тока, активные, индуктивные и емкостные сопротивления (данные к задаче выбираются согласно последней цифре шифра студента).
Требуется определить:
1. Показания электроизмерительных приборов включенных в цепь: амперметра, вольтметра, ваттметра и фазометра.
2. Построить векторную диаграмму токов.
Методические рекомендации по решению задачи 2.
Вторая задача относится к расчету однофазной цепи переменного тока с последовательно-параллельным соединением резисторов, индуктивных катушек и конденсаторов. Для её решения предварительно нужно изучить § 5.9, § 5.10 из [2], с. 73...77.
Даны численные значения сопротивлений R1, R2 XL1, XL2, XC1, XC2. Заданы также входное напряжение U или входной ток I в действующих значениях (табл. 2).
Данную задачу можно решать методом проводимостей, поэтому необходимо определить сначала активные проводимости ветвей gi и всей цепи g, индуктивные проводимости ветвей bLj и всей цепи bL, ёмкостные проводимости ветвей bСk и всей цепи bС , полную проводимость всей цепи у. Если рассматриваемая ветвь содержит сопротивления какого-либо вида Ri, XLi, XCi, то проводимости вычисляются по формулам:
 . (16)
. (16)
Если рассматриваемая ветвь содержит два и более последовательно соединенных разнотипных элементов, то проводимость i-той ветви вычисляется по формулам:
 , (17)
, (17)
где Zi - полное сопротивление i-той ветви.
Рис 2. Принципиальные электрические схемы к задаче 2.
Таблица 2 – Исходные данные к задаче 2
| Варианты | Данные для расчёта | ||||||||
| Предпоследняя цифра шифра | Последняя цифра шифра | U | I | R1 | R2 | XL1 | XL2 | XC1 | XC2 |
| В | А | Ом | Ом | Ом | Ом | Ом | Ом | ||
| 0…1 схема №1 | 0...1 | - | - | ||||||
| 2…3 | - | - | |||||||
| 4…5 | - | - | |||||||
| 6…7 | - | - | |||||||
| 8…9 | - | - | |||||||
| 2…3 схема №2 | 0...1 | - | 0,5 | - | |||||
| 2…3 | - | 1,0 | - | ||||||
| 4…5 | - | 1,5 | - | ||||||
| 6…7 | - | 2,0 | - | ||||||
| 8…9 | - | 2,5 | - | ||||||
| 4…5 схема №3 | 0...1 | - | - | - | |||||
| 2…3 | - | - | - | ||||||
| 4…5 | - | - | - | ||||||
| 6…7 | - | - | - | ||||||
| 8…9 | - | - | - | ||||||
| 6…7 схема №4 | 0...1 | - | - | - | |||||
| 2…3 | - | - | - | ||||||
| 4…5 | - | - | - | ||||||
| 6…7 | - | - | - | ||||||
| 8…9 | - | - | - | ||||||
| 8…9 схема №5 | 0...1 | - | - | - | |||||
| 2…3 | - | - | - | ||||||
| 4…5 | - | - | - | ||||||
| 6…7 | - | - | - | ||||||
| 8…9 | - | - | - |
Активная, индуктивная, ёмкостная проводимости всей цепи вычисляется по формулам:
 . (18)
. (18)
Полная проводимость всей цепи определяется по формуле:
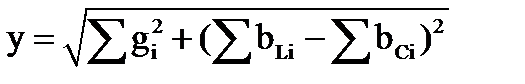 . (19)
. (19)
Входной ток I определяется по закону Ома:
I = U·у. (20)
Входное напряжение по заданному току вычисляется из формулы (20).
Показания ваттметра и фазометра вычисляются по соответствующим формулам:
 ; (21)
; (21)
 . (22)
. (22)
Примечание. Для некоторых вариантов показание фазометра вычисляется по формуле:
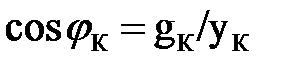 , (23)
, (23)
где qК - общая активная проводимость к-го участка цепи, содержащего одну или две параллельные ветви, См;
yК - полная проводимость к-го участка цепи, См.
При построении векторной диаграммы токов необходимо выполнить:
1) записать для данной цепи векторное уравнение токов на основе 1-го закона Кирхгофа:
Ī= Ī1 + Ī2 + Ī3 +…+Īi, (24)
где Ī1, Ī2, Ī3,…Īi - векторы общего тока и токов ветвей заданной цепи.
Численные значения токов ветвей определяют на основе закона Ома:
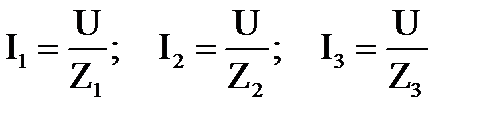 , (25)
, (25)
где Z1, Z2, Z3 - полные сопротивления ветвей, Ом;
2) выбрать базовый вектор, относительно которого строится диаграмма токов, в параллельной цепи это вектор напряжения Ū;
3) фазовые углы между векторами токов и вектором напряжения можно определять по формуле:
 , (26)
, (26)
где Zi- полное сопротивление соответствующей ветви, Ом;
Ri - сумма активных сопротивлений ветви, Ом.
Задача 3
Однофазные токоприемники соединены способом «звезда» и включены в трехфазную сеть с линейным напряжением U. Тип сопротивлений, их численное значение, а также линейное напряжение U заданы в табл. 3. Приемники фаз А, В, С соединены последовательно или параллельно согласно принципиальным электрическим схемам (рис. 3).
Требуется определить:
1. Силу токов IА, IВ, IС в фазах токоприемников А, В, С.
2. Активную, реактивную, полную мощность каждой фазы в отдельности, а также активную, реактивную и полную мощность всех трех фаз.
3. Построить векторную диаграмму токов и напряжений и графически определить силу тока IN в нейтральном проводе.
Методические рекомендации по решению задачи 3.
Третья задача относится к расчету трехфазных цепей переменного тока, в которых потребители соединены способом «звезда».
Для её решения необходимо изучить § 7.1...§ 7.3 из [1] или § 4.1... § 4.4 из [2], стр. 104...114.
Дана трехфазная четырехпроводная несимметричная цепь с последовательно или параллельно соединенными элементами (активными и реактивными). Задано входное линейное напряжение.
Для определения линейного (фазного) тока IА, IВ, IС необходимо найти полное сопротивление фазы Zi, если элементы соединены последовательно, или полную проводимость фазы Уi, если элементы соединены параллельно. Тогда токи определяются по формулам:
 , (27)
, (27)
или
IА = UА·УА; IВ = UВ·УВ; IС = UС·УС, (28)
где UА, UВ, UС - фазное напряжение цепи, В;
ZА, ZВ, ZС, УА, УВ, УА - полные сопротивления или проводимости фаз (смотри задачи 1, 2).
Рис 3. Принципиальные электрические схемы к задаче 3.
Таблица 3 – Исходные данные к задаче 3
| Варианты | Данные для расчёта | |||||||||
| Предпоследняя цифра шифра | Последняя цифра шифра | UЛ | RА | RВ | RС | XLА | XLB | XLС | XСА | XCВ |
| В | Ом | Ом | Ом | Ом | Ом | Ом | Ом | Ом | ||
| 0…1 схема №1 | 0...1 | - | - | - | ||||||
| 2…3 | - | - | - | |||||||
| 4…5 | - | - | - | |||||||
| 6…7 | - | - | - | |||||||
| 8…9 | - | - | - | |||||||
| 2…3 схема №2 | 0...1 | - | - | - | - | |||||
| 2…3 | - | - | - | - | ||||||
| 4…5 | - | - | - | - | ||||||
| 6…7 | - | - | - | - | ||||||
| 8…9 | - | - | - | - | ||||||
| 4…5 схема №3 | 0...1 | - | - | - | - | - | ||||
| 2…3 | - | - | - | - | - | |||||
| 4…5 | - | - | - | - | - | |||||
| 6…7 | - | - | - | - | - | |||||
| 8…9 | - | - | - | - | - | |||||
| 6…7 схема №4 | 0...1 | - | ||||||||
| 2…3 | - | |||||||||
| 4…5 | - | |||||||||
| 6…7 | - | |||||||||
| 8…9 | - | |||||||||
| 8…9 схема №5 | 0...1 | - | - | - | ||||||
| 2…3 | - | - | - | |||||||
| 4…5 | - | - | - | |||||||
| 6…7 | - | - | - | |||||||
| 8…9 | - | - | - |
Активная мощность фазы в случае последовательно или параллельно соединенным элементам вычисляется по формулам:
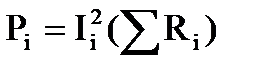 или
или  , (29)
, (29)
где SRi - сумма активных сопротивлений фазы, Ом;
gi - активная проводимость фазы, См.
Индуктивная мощность фазы QLi и емкостная мощность фазы QCi определяются аналогично, только нужно подставлять вместо Ri и gi соответственно XLi, XCi, ВLi, ВCi.
Полная мощность фазы Si вычисляется по формуле (9), исключая при этом ненужные слагаемые.
Активная мощность всей цепи вычисляется по формуле:
Р =SРi. (30)
Реактивная мощность всей цепи вычисляется по формуле:
Q = SQLi – SQCi. (31)
Полная мощность всей цепи определяется по формуле:
 (32)
(32)
Для построения векторной диаграммы линейных и фазных напряжений и токов необходимо определить углы сдвига между фазными напряжениями и соответствующими фазными токами для всех трех фаз.
Если элементы фазы соединены последовательно, то угол вычисляется по формуле:
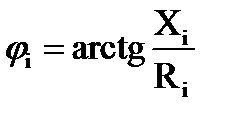 , (33)
, (33)
где Ri - активное сопротивление i-ой фазы, Ом;
Xi - реактивное сопротивление i-той фазы, Ом.
Примечание. Реактивное сопротивление каждой фазы вычисляется по формуле:
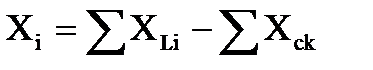 . (34)
. (34)
Если сопротивления фазы соединены параллельно, то угол ji определяется по формуле:
 , (35)
, (35)
где gi - активная проводимость i-ой фазы, См;
bi - реактивная проводимость i-ой фазы, См.
Примечание. Реактивная проводимость i-ой фазы вычисляется по формуле:
 . (36)
. (36)
При построении векторной диаграммы необходимо выполнить следующие операции:
1) записать для данной цепи одно векторное уравнение по первому закону Кирхгофа для токов и три векторных уравнения для напряжений по второму закону Кирхгофа:
IА+ IВ+IС=IN (37)
 (38)
(38)
2) векторную диаграмму напряжений начинать с построения симметричной звезды векторов фазных напряжений ŪА, ŪВ, ŪС. Линейные напряжения ŪАВ, Ūвс, ŪСА строить как векторные разности соответствующих фазных напряжений (38);
3) линейные (фазные) токи ĪА, ĪВ, ĪС нужно строить под соответствующими фазовыми углами ji, относительно своих фазных напряжений;
4) вектор тока ĪN в нейтральном проводе получить на диаграмме согласно уравнению (37).
Задача 4
Трехфазный понижающий силовой трансформатор имеет технические данные, приведенные в табл. 4: номинальную мощность Sн, номинальное высшее линейное напряжение U1Л, номинальное низшее линейное напряжение U2Л, мощность потерь холостого хода (при номинальном напряжении) РО, мощность потерь короткого замыкания (при номинальном токе) РК, схемы соединения первичных и вторичных обмоток трансформатора (рис. 4).
Требуется определить:
1. Линейный и фазный коэффициенты трансформации трансформатора.
2. Фазные напряжения трансформатора.
3. Линейные и фазные токи трансформатора.
4. Коэффициент полезного действия при коэффициенте мощности нагрузки cosjм = 0,9 и коэффициенте нагрузки b = 75% от номинальной.
5. Годовой коэффициент полезного действия при полной нагрузке b = 1 и коэффициенте мощности cosjм = 0,8, времени работы под нагрузкой в году Т = 7000 ч.
6. Построить векторную диаграмму линейных и фазных напряжений для первичных и вторичных обмоток трансформатора и определить группу соединения обмоток.
Методические рекомендации по решению задачи 4.
Четвертая задача относится к расчету трехфазного силового трансформатора, способ соединения обмоток которого задан. Для решения задачи необходимо изучить §13.10 из [1] или §9.8 из [2], стр. 248…255.
Распространенными схемами соединения обмоток трансформаторов являются схема «звезда», обозначаемая буквой У (или символом Y), и схема «треугольник», обозначаемая буквой Д (или символом D).
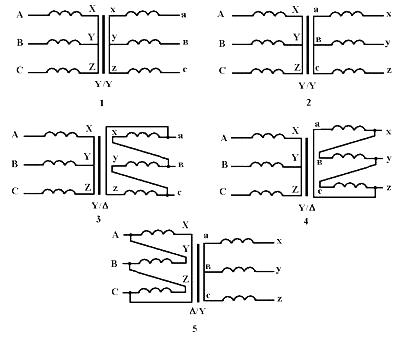
Рис 4. Принципиальные электрические схемы к задаче 4.
Таблица 4 – Исходные данные к задаче 4
| Варианты | Данные для расчёта | ||||||
| Предпоследняя цифра шифра | Последняя цифра шифра | S | U1Л | U2Л | РО | РК | Схема соединения обмоток |
| кВА | кВ | кВ | кВт | кВт | |||
| 0…1 схема №1 | 0...1 | 0,25 | 0,12 | 0,6 | U/U | ||
| 2…3 | 0,4 | 0,12 | 0,6 | ||||
| 4…5 | 0,25 | 0,17 | 0,88 | ||||
| 6…7 | 0,4 | 0,17 | 0,88 | ||||
| 8…9 | 0,25 | 0,25 | 1,28 | ||||
| 2…3 схема №2 | 0...1 | 0,25 | 0,44 | 1,97 | U/U | ||
| 2…3 | 0,4 | 0,44 | 1,97 | ||||
| 4…5 | 0,25 | 0,54 | 2,75 | ||||
| 6…7 | 0,4 | 0,54 | 2,75 | ||||
| 8…9 | 0,25 | 0,66 | 2,75 | ||||
| 4…5 схема №3 | 0...1 | 0,25 | 1,08 | 5,5 | U/D | ||
| 2…3 | 0,4 | 1,08 | 5,5 | ||||
| 4…5 | 0,25 | 1,35 | 5,5 | ||||
| 6…7 | 0,4 | 1,35 | 5,5 | ||||
| 8…9 | 0,4 | 1,6 | 7,6 | ||||
| 6…7 схема №4 | 0...1 | 0,4 | 2,75 | 12,2 | U/D | ||
| 2…3 | 6,5 | 2,75 | 12,2 | ||||
| 4…5 | 0,4 | 4,5 | |||||
| 6…7 | 6,5 | 4,5 | |||||
| 8…9 | 0,4 | 4,95 | 16,5 | ||||
| 8…9 схема №5 | 0...1 | 6,5 | 8,5 | 33,5 | D/U | ||
| 2…3 | 6,5 | 9,5 | 33,5 | ||||
| 4…5 | 10,5 | 9,5 | 33,5 | ||||
| 6…7 | 6,5 | 12,3 | |||||
| 8…9 | 6,5 | 13,5 | 46,5 |
Обмотка высшего напряжения (ВН) может быть соединена или в «звезду» или в «треугольник» независимо от способа соединения обмотки низшего напряжения (НН). Очевидно, что число основных схем соединения обмоток равно четырем, а именно Y/Y , D/D , Y/D, D/Y. Здесь над чертой показано обозначение схемы соединения обмоток ВН, под чертой – обмоток НН. Начала обмоток ВН обозначаются заглавными латинскими буквами А, В, С; концы этих же обмоток буквами Х, У, Z. Начала обмоток НН обозначаются прописными латинскими буквами а, в, с; концы – x, y, z.
Разнообразие схем и способов соединений обмоток приводит к необходимости указывать численное значение фазового угла между векторами линейных одноименных напряжений обмоток ВН и НН трансформатора. Фазовые углы определяют так называемые группы соединения обмоток. Всего насчитывается двенадцать групп от 0 до 11 включительно.
Трехфазные трансформаторы имеют два коэффициента трансформации – линейный и фазный. Линейный коэффициент определяется как отношение линейного напряжения U1л (U1н) обмотки ВН к линейному напряжению U2л (U2н) обмотки НН:
 . (39)
. (39)
Фазный коэффициент трансформации равен отношению фазного напряжения обмотки ВН U1ф к фазному напряжению обмотки НН U2ф:
 . (40)
. (40)
При соединении обмоток по способу «звезда» используют формулы:
 , (41)
, (41)
IЛ=IФ. (42)
При соединении обмоток по способу «треугольник» используют формулы:
UЛ=UФ, (43)
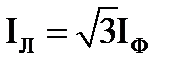 . (44)
. (44)
Для определения токов обмоток ВН и НН используют формулы полной мощности трансформатора:
S1Н=S2Н , (45)
или
 . (46)
. (46)
Коэффициент полезного действия трансформатора можно определять по формуле:
 , % (47)
, % (47)
где cos j2 – коэффициент активной мощности потребителя;
Ро – мощность потерь холостого хода, кВт;
Рк – мощность потерь короткого замыкания, кВт;
b – коэффициент нагрузки трансформатора.
Его можно определить по формуле:
 . (48)
. (48)
Годовой к. п. д. учитывает экономичность работы трансформатора за год:
 , % (49)
, % (49)
где То = 8760 ч, Т=7000 ч.
При построении векторной диаграммы напряжений трансформатора с высшей и низшей сторон необходимо:
1) построить векторную диаграмму линейных и фазных напряжений обмоток ВН: ŪАХ, ŪВY, ŪСZ, ŪАВ, ŪВС, ŪСА. Следует учитывать, что при соединении обмоток трансформатора в треугольник линейные напряжения равны фазным;
2) построить векторную диаграмму линейных и фазных напряжений обмоток НН: Ūax, Ūвy, Ūсz, Ūав, Ūвс, Ūса. Векторы одноименных фазных напряжений обмоток ВН и НН параллельны между собой, например ŪАХïïŪax, ŪВYïïŪвy, ŪСZïïŪсz;
3) для определения группы соединения обмоток трансформатора нужно по векторной диаграмме вычислить, фазовый угол между одноименными линейными векторами напряжений обмоток ВН и НН, например, угол между векторами ŪАВ и Ūав. Число получающееся в результате деления значений этого угла на 300 и дает искомую группу соединения обмоток трансформатора.
Примечание. Фазовый угол сдвига следует отсчитывать от вектора линейного напряжения обмотки ВН до одноименного вектора линейного напряжения обмотки НН по часовой стрелке.
Примеры решения задач
Задача 1. В сеть с переменным синусоидальным напряжением U = 120 В, частотой f = 50 Гц последовательно включены: L = 38 мГн; R1 = 5 Ом; R2 = 3 Ом; C = 177 мкФ.
Определить показания измерительных приборов амперметра, вольтметра, ваттметра и фазометра (рис. 5), резонансную частоту fо, построить векторную диаграмму напряжений.
Рис 5. Принципиальная электрическая схема к решению задачи 1.
Р е ш е н и е
1. Сопротивление индуктивной катушки:
XL = 2pfL = 2·3,14·50·0,038 = 12 Ом.
2. Сопротивление конденсатора:

3. Полное сопротивление цепи:

4. Показание амперметра:
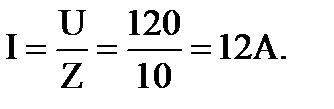
5. Показание ваттметра:
Р = I2·(R1+ R2) = 102·(5 + 3) = 800 Вт.
6. Показание вольтметра на участке цепи:
 В.
В.
7. Показание фазометра:

8. Значение резонансной частоты:
 Гц.
Гц.
9. Для построения векторной диаграммы выберем масштабы mU, В/мм, mI, А/мм и вычислим напряжение на отдельных элементах цепи:
UL = XL I = 12 · 2 = 144 В;
UR1 = R1 I = 5 · 12 = 60 В;
UR2 = R2 I = 3 · 12 = 36 В;
UC = XC I = 18 · 12 = 216 В.
Векторная диаграмма в выбранном масштабе построена на рис. 6.
Рис 6. Векторная диаграмма к решению задачи 1.
Векторы напряжений на активных сопротивлениях ŪR1 и ŪR2 совпадают по направлению с вектором тока Ī, вектор ŪL опережает, а вектор ŪC отстает от вектора тока Ī на четверть периода или 900. Вектор напряжения на зажимах цепи U равен геометрической сумме напряжений на всех ее элементах.
Задача 2. В сеть с переменным синусоидальным напряжением U = 20 В, частотой f = 50 Гц параллельно включены R1 = 3 Ом, XL = 4 Ом, R2 = 4 Ом, XC = 3 Ом, R3 = 4 Ом (рис. 7).
Рис 7. Принципиальная электрическая схема к решению задачи 2.
Определить показания измерительных приборов амперметра, ваттметра, фазометра, построить векторную диаграмму токов.
Р е ш е н и е
1. Активная проводимость первой ветви:
 См.
См.
2. Индуктивная проводимость первой ветви:

3. Активная проводимость второй ветви:
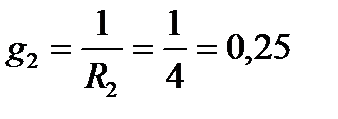 См.
См.
4. Емкостная проводимость третьей ветви:

5. Активная проводимость третьей ветви:
 См.
См.
6. Активная проводимость всей цепи:
g = g1 + g2 + g3 = 0,12 + 0,25 + 0,16 = 0,53 Cм.
7. Индуктивная проводимость всей цепи:
bL = 0,16 Cм.
8. Емкостная проводимость всей цепи:
bС = 0,12 Cм.
9. Полная проводимость всей цепи:
 См.
См.
10. Показание амперметра:
I = U · y = 20 · 0,53 = 10,6 А.
11. Показание ваттметра:
Р = U2 · g = 202 · 0,53 = 212 Вт.
12. Показание фазометра:
α = arccos (g/y) = arccos (0,53/0,53) = arccos 1 = 0°
13. Для построения векторной диаграммы выберем масштабы: mU, В/мм, mI, А/мм и вычислим составляющие общего тока
I1a = U · g1 = 20 · 0,12 = 2,4 A;
I2a = U · g2 = 20 · 0,25 = 5 A;
I3a = U · g3 = 20 · 0,16 = 3,2 A;
I1L = U · bL = 20 · 0,16 = 3,2 A;
I3C = U · bC = 20 · 0,12 = 2,4 A.
Векторная диаграмма в выбранном масштабе построена на рис. 8.
Рис 8. Векторная диаграмма к решению задачи 2.
Векторы Ī1а, Ī2а, Ī3а, совпадают по фазе с вектором напряжения Ū, вектор Ī1L, отстает, а вектор Ī3C опережает вектор Ū на четверть периода. Вектор общего тока Ī равен геометрической сумме составляющих векторов токов.
Задача 3. Однофазные токоприемники RA = XA = RB = XC = 10 Ом соединены по способу «звезда» и включены в сеть с линейным напряжением U = 220 В (рис. 9).
Определить силу тока в фазах А, В, С; активную, реактивную и полную мощность каждой фазы в отдельности; активную, реактивную и полную мощность всех трех фаз.
Построить векторную диаграмму токов и напряжений и графически определить силу тока в нейтральном проводе.
Рис 9. Принципиальная электрическая схема к решению задачи 3.
Р е ш е н и е
1. Активная проводимость фазы А:
 См.
См.
2. Индуктивная проводим ость фазы А:
 См.
См.
3. Полная проводимость фазы А:
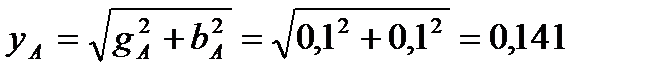 См.
См.
4. Ток фазы А:
IA = UA·УA = 127·0,141 = 17,9 А.
5. Ток фазы В:

6. Ток фазы С:

7. Активная мощность фазы А:
РА = UА2 · gA = 1272 · 0,1 = 1613 Вт.
8. Активная мощность фазы В:
PB = IB2· RB= 12,72 · 10 = 1613 Вт.
9. Индуктивная мощность фазы А:
QA = UA · bA = 127 · 0,1 = 1613 вар.
10. Емкостная мощность фазы С:

11. Активная мощность всей цепи:
Р = РА + РВ = 1613 + 1613 = 3226 Вт.
12. Реактивная мощность всей цепи:
Q = QА – QС = 1613 – 1613 = 0.
13. Полная мощность всей цепи:

14. Для построения векторной диаграммы напряжений и токов выберем масштабы: mU,В/мм, mI, А/мм и определим углы сдвига между вектором фазного напряжения и соответствующим ему вектором фазного тока:

Векторная диаграмма в выбранном масштабе построена на рис. 10.
Рис 10. Векторная диаграмма к решению задачи 3.
Вектор ĪN найден путем сложения векторов ĪА, ĪВ, ĪС.
Задача 4. Трехфазный понижающий силовой трансформатор имеет следующие технические данные: SН = 25 кВА; U1Н = 6 кВ; U2Н = 0,23 кВ; РО = 0,12 кВт; РК = 0,6 кВт; способ соединения обмоток (рис. 11), D/U.
Определить линейный и фазный коэффициенты трансформации, фазные напряжения, линейные и фазные токи, коэффициент полезного действия при сosj2 = 0,8 и коэффициенте нагрузки b = 80% от номинальной. Определить также годовой коэффициент полезного действия при полной нагрузке b = 1, при сosj2 = 0,9 и времени работы Т = 5000 ч. Построить векторную диаграмму линейных и фазных напряжений трансформатора, определить группу соединения обмоток трансформатора.
Рис 11. Принципиальная электрическая схема к решению задачи 4.
Р е ш е н и е
1. Линейный коэффициент трансформации:

2. Фазный коэффициент трансформации:
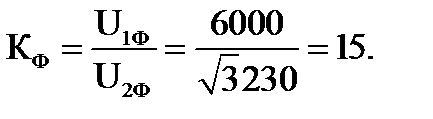
3. Фазное напряжение обмотки ВН:

4. Фазное напряжение обмотки НН:
U2Ф=U2Н=0,23 кВ.
5. Линейный ток обмотки ВН:

6. Фазный ток обмотки ВН:
I1Ф=I1Л=2,40 А.
7. Линейный ток обмотки НН:
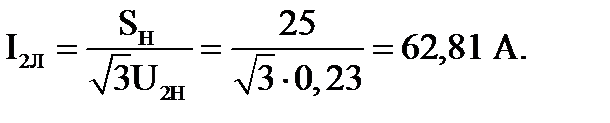
8. Фазный ток обмотки НН:
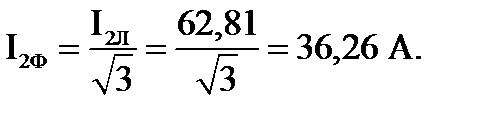
9. Коэффициент полезного действия:
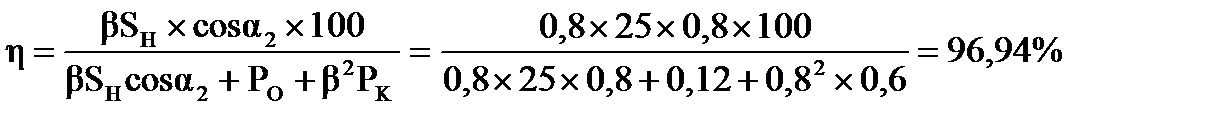
10. Годовой коэффициент полезного действия:

11. Для построения векторной диаграммы напряжений выберем разные масштабы напряжений обмоток ВН и НН, mUBН, кВ/мм, mUHH, кВ/мм. Векторы линейных (фазных) напряжений обмоток НН параллельны векторам фазных напряжений обмоток ВН (рис. 12 а).
Рис 10. Векторные диаграмма к решению задачи 4.
Из векторной диаграммы номер группы трансформатора определяется делением фазового угла сдвига между векторами ŪАВ и Ūав на 300, в результате имеем единицу, то есть первую группу трансформатора Y/D-1 (см. рис.12 б.).
ЛИТЕРАТУРА
1. Электротехника. Под ред. В.Г. Герасимова. М.: Высшая школа, 1985. 480 с.
2. Борисов Ю.М. и др. Электротехника М.: Энергоатомиздат, 1985. 450 с.
3. Справочное пособие по электротехнике и основам электроники. Под ред. А.В. Нетушила. М.: Высшая школа, 1985. 320 с.
4. Основы промышленной электроники. Под ред. В.Г. Герасимова. М.: Высшая школа, 1986, 336 с.
5. Сборник задач по электротехнике и основам электроники. Под ред. В.Г. Герасимова. М.: Высшая школа, 1987. 288 с.
6. Морозов А.Г. Электротехника, электроника и импульсная техника. М.: Высшая школа, 1987. 217 с.
7. П р и щ е п Л.Г. Учебник сельского электрика. М.: Агропромиздат, 1986. 587 с.
8. Электротехнический справочник (в трех томах). Под общ. ред. В.Г. Герасимова и др. М.: Энергоатомиздат, 1985 1986, 1988.
Учебно-методическое издание
Дата добавления: 2015-04-16; просмотров: 154; Мы поможем в написании вашей работы!; Нарушение авторских прав |