Эквипотенциальные поверхности и поверхности равного давления.

Поверхности, в каждой точке которых 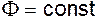, называют эквипотенциальными. Частным случаем эквипотенциальной поверхности является поверхность равного давления, т.е. поверхность, в каждой точке которой 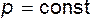. В этом случае 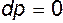и (3.4) принимает вид

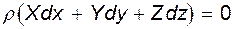
Но плотность 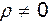, и, следовательно,

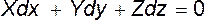(3.8)

Уравнение (3.8) называют уравнением поверхности равного давления. Если из массовых сил на жидкость действует только сила тяжести, то 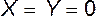; 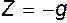(знак минус, т.к. сила тяжести ориентирована в сторону, противоположную оси z); 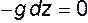и 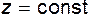, т.е. в покоящейся жидкости любая горизонтальная плоскость есть поверхность равного давления.

3.4. Равновесие однородной несжимаемой жидкости в поле сил тяжести. Закон Паскаля. Гидростатичес­кий закон распределения давления.

Проинтегрируем основное уравнение гидростатики (3.4) в предположении, что 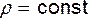(жидкость несжимаема) и считая, что из массовых сил действует только сила тяжести. Как показано выше, в этом случае 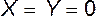, , 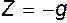т.е. 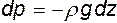, и после интегрирования

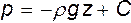(3.9)

где C - произвольная постоянная. Для ее нахождения используем следующее граничное условие (см. рис. 3.1): при 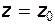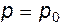. Из (3.9) следует, что

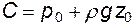
И после подстановки

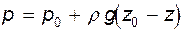(3.10)

Как видно из рис. 3.1, разность ( 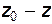) - глубина погружения рассматриваемой частицы, которую будем обозначать буквой h, т.е.

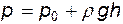(3.11)

Полученное уравнение выражает известный из курса физики закон Паскаля: давление, приложенное к свободной поверхности, передается во все точки без изменения.

Поскольку любое правильное физическое уравнение должно быть размерностно однородным, то ясно, что член 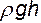должен выражаться в единицах давления, т.е. в паскалях (Па - Н/м2). Эту величину называют избыточным давлением. Она может быть как положительной, так и отрицательной. Такая трактовка приводит нас к понятию абсолютного давления, которое в соответствии с (3.11) может быть представлено как сумма барометрического (атмосферного) давления и избыточного, т.е.

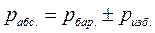(3.12)

Отрицательное избыточное давление называют вакуумом.

Вернемся вновь к уравнению (3.10). После деления обеих его частей на 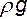получаем

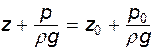(3.13)

В таком виде все его члены выражаются в единицах длины и носят название напоров. Величина z характеризует положение жидкой частицы над произвольно выбираемой горизонтальной плоскостью отсчета, т.е. z - это геометрический напор; 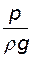- пьезометрический напор. Сумму этих величин 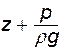называют гидростатическим напором. Чтобы уяснить физический смысл этих величин, рассмотрим простую схему, показанную на рис. 3.2.

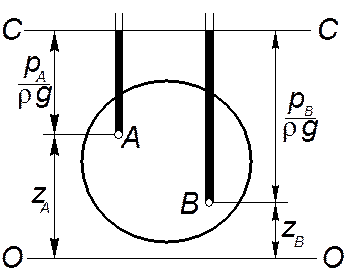
Представим герметично закрытый сосуд, заполненный жидкостью, находящейся под давлением. Выберем в этом сосуде две произвольно рас­положенные точки A и B и, опять-таки произвольно, горизонтальную плоскость O-O, которую назовем плоскостью отсчета.

Координаты частиц, расположенных в точках A и B будут 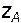и 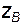. В соответствии со сказанным выше, величины 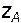и 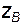выражают геометрический напор. Введем теперь через крышку сосуда в точки A и B сообщенные с атмосферой стеклянные трубки. Эти трубки называют пьезометрами. Поскольку по условию жидкость находится под давлением, то она начнет подниматься по пьезометрам. Не представляет труда и ответ на вопрос о том, когда прекратится подъем. Очевидно, что это произойдет в тот момент, когда высота столба жидкости уравновесит давление в рассматриваемой точке. Это и есть пьезометрическая высота, либо пьезометрический напор.

Соотношение (3.13) справедливо для любых произвольно выбранных частиц покоящейся жидкости, поэтому в общем виде его можно записать как 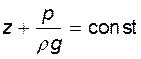, т.е. для любых точек жидкости гидростатический напор одинаков. Следовательно, уровни в пьезометрах установятся на одной и той же высоте (плоскость C-C на рис. 3.2). Уравнение (3.13) выражает так называемый гидростатический закон распределения давления.