Система уравнений Максвелла для электромагнитного поля

43. Вихревое электрическое поле.

Для объяснения возникновения индукционного тока в неподвижных проводниках (второй опыт Фарадея) Максвелл предположил, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре (первое основное положение теории Максвелла).

Циркуляция вектора напряженности этого поля

По определению поток вектора 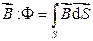откуда следует

Здесь и в дальнейшем мы используем частную производной по времени, поскольку в общем случае электрическое поле может быть неоднородным, и может зависеть не только от времени, но и от координат.

Таким образом, циркуляция вектора не равна нулю, т.е.

электрическое поле , возбуждаемое переменным магнитным полем, как и само магнитное поле, является вихревым.

Суммарное электрическое поле складывается из электрического поля, создаваемого зарядами 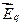и вихревого электрического поля . Поскольку

циркуляция равна нулю, то циркуляция суммарного поля

Это - первое уравнение системы уравнений Максвелла для электромагнитного поля.

44.Ток смещения.

Максвелл предположил, что аналогично магнитному полю и всякое изменение электрического поля вызывает в окружающем пространстве вихревое магнитное поле (второе основное положение теории Максвелла).

Поскольку магнитное поле есть основной, обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения, в отличие от тока проводимости, обусловленного движением заряженных частиц.

Надо сказать, что термин ток смещения не является удачным. Он имеет некоторое основание в случае диэлектриков, так как в них действительно смещаются заряды в атомах и молекулах. Однако понятие тока смещения применяется и для полей в вакууме, где никаких зарядов, а следовательно и никакого их смещения нет. Тем не менее этот термин сохранился в силу исторических традиций.

Плотность тока смещения

Следует подчеркнуть, что ток смещения определяется производной

вектора 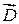, но не самим вектором 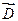. Так, например, в поле плоского конденсатора вектор 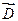всегда направлен от положительной пластины к отрицательной. Но в случае, если электрическое поле возрастает, то , а следовательно и ток смещения направлены так, как показано на рисунке (а). Если же электрическое поле убывает, то направлено от отрицательной пластины к положительной, и магнитное поле противоположно (рис. (б)) по сравнению с первым случаем.

Если в каком-либо проводнике имеется переменный ток, то внутри проводника существует переменное электрическое поле. Поэтому внутри проводника имеется и ток проводимости, и ток смещения и магнитное поле проводника определяется суммой этих двух токов.

Максвелл ввел понятие полного тока, равного сумме токов проводимости и смещения. Плотность полного тока

Полный ток всегда замкнут. На концах проводников обрывается лишь ток проводимости, а в диэлектрике (или в вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.

Из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно - способность создавать в окружающем пространстве магнитное поле.

Максвелл обобщил теорему о циркуляции вектора , использовав полный ток

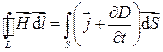
Обобщенная теорема о циркуляции вектора представляет собой второе уравнение системы уравнений Максвелла для электромагнитного поля.

45. Полная система уравнений Максвелла.

Третье уравнение системы уравнений Максвелла для электромагнитного поля это теорема Гаусса для поля Для заряда, непрерывно

распределенного внутри замкнутой поверхности с объемной плотностью р, это уравнение имеет вид

Четвертое уравнение Максвелла - это теорема Гаусса для поля В

Таким образом, система уравнений Максвелла в интегральной форме

Для того, чтобы эта система уравнений была полной ее необходимо дополнить такими соотношениями, в которые входили бы величины, характеризующие индивидуальные свойства среды, в которой возбуждаются электрические и магнитные поля. Эти соотношения называются материальными соотношениями

, ,

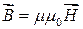Где ε₀ и µ₀- соответственно электрическая и магнитная постоянные, ε и µ - соответственно диэлектрическая и магнитная проницаемости, γ - удельная проводимость вещества.

Из уравнений Максвелла следует, что

-- источниками электрического поля являются либо электрические заряды, либо изменяющиеся во времени магнитные поля,

-- магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями,

-- переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом - они образуют единое электромагнитное поле.

Для стационарных полей (Е = const и В = const) уравнения Максвелла имеют вид

В этом случае электрические и магнитные поля независимы друг от друга, что позволяет изучать отдельно постоянные электрическое и магнитное поле.

Воспользуемся известными из векторного анализа теоремами Стокса и Гаусса

По определению, дивергенцией и ротором векторного поля в данной точке М называют следующие производные по объёму
,

где интегралы и есть, соответственно, скалярный и векторный потоки векторного поля через замкнутую поверхность S, которая окружает данную точку М , охватывая область с объёмом V.

Дивергенция есть мера источников поля. Если в некоторой области дивергенция равна нулю, то векторное поле в этой области свободно от источников. Те точки поля в которых дивергенция положительна называются источниками поля, а в которых отрицательна - стоками векторного поля.

Используя теоремы Стокса и Гаусса, можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства)

Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

Так, например, уравнение явно демонстрирует, что источниками

электрического поля являются положительные электрические заряды, а стоками - отрицательные электрические заряды. Уравнение отражает

тот факт, что не существует источников и стоков магнитного поля - "магнитных зарядов".

В случае если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла - интегральная и дифференциальная - эквивалентны. Однако если имеются поверхности разрыва - поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Для того чтобы эти уравнения Максвелла в дифференциальной форме были справедливы и на границах сред, где величины, входящие в уравнения, меняются скачкообразно, необходимо дополнить эти уравнения граничными условиями, которым должно удовлетворять магнитное поле на границе раздела двух сред. Эти соотношения были рассмотрены ранее:

D_n1=D_n2 , E_τ1= E_τ1 , B_n1=B_n2 , H_τ1= H_τ1

(первое и последнее уравнения выведены для случая, когда на границе раздела нет ни свободных зарядов, ни токов проводимости).

КОЛЕБАНИЯ И ВОЛНЫ