Нц повторять. Команды, повторяемые в цикле

Команды, повторяемые в цикле

кцпокане Условие окончания цикла.

Запишем алгоритм вычисления интеграла с заданной точностью на алгоритмическом языке, используя введенную команду цикла с постусловием:

алг Метод Симпсона с автоматическим выбором шага (аргвещ a, b, , резвещ )

начвещ , h, , ; цел m, i

| Задание начального значения параметра m

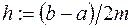; | Вычисление соответствующего

| значения шага интегрирования

= ; | Вычисление

|начального значения

|

нцповторять | Начало цикла метода повторного счета

; | Передача значения с предыдущего

| шага цикла или начального значения.

; | Изменение значения параметра m.

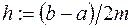; | Вычисление соответствующего

| значения шага интегрирования

:=0;

нцдля i от 1 до m-1

| Вычисление суммы

|

Кц

:=0;

нцдля i от 1 до m

| Вычисление суммы

|

Кц

| Вычисление

| =

кцпокане | Конец цикла метода

| повторного счета

Кон

3. Записать формулу Гаусса с 3-мя узлами для вычисления интеграла и найти оценку абсолютной погрешности вычисленного по этой формуле приближенного значения интеграла для случая, когда , , .

Решение:

Запишем формулу Гаусса с 3-мя узлами. При n=3 формула Гаусса на имеет 3 узла , , , и три коэффициента , .

Узлы формулы Гаусса на равны

,

,

.

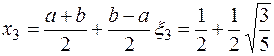Коэффициенты формулы Гаусса на равны

, , .

Формула Гаусса в нашем случае примет вид

При вычислении по этой формуле получается приближенное значение интеграла Q. Найдем оценку его абсолютной погрешности

,

где - мажорантная оценка модуля производной на ( ).

Найдем . Для этого найдем производную . На , очевидно, выполняется: . Отсюда =720.

Вычислим оценку погрешности приближенного значения интеграла:

.

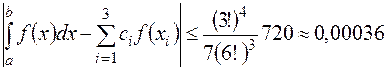4. Составить алгоритм вычисления приближенного значения интеграла методом Монте-Карло (первая схема) с погрешностью, не превышающей заданного положительного числа с вероятностью 0,997. Записать алгоритм на алгоритмическом языке.

Решение:

Исходными данными для алгоритма являются значения a, b, и функция . Первая алгоритмическая схема метода Монте-Карло состоит в последовательном вычислении значений при до тех пор, пока не будет выполнено условие

. Здесь - значения случайной величины (равномерно распределенной на ), получаемые с помощью датчика случайных чисел. Последнее вычисленное значение даст нам искомое приближенное значение интеграла.

В этих формулах содержатся суммы, число членов которых растет с ростом n. Чтобы избавиться от лишних вычислений, мы будем вычислять величины и 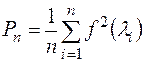по рекуррентным формулам:

, .

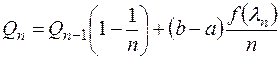По этим формулам будут вычисляться значения этих величин в цикле при 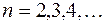Для того чтобы по этим формулам можно было начать счет, до начала цикла необходимо вычислить , .Вычислив и , величину удобно выразить через них:

.

Поскольку на каждом шаге цикла нужно только одно значение каждой из величин , и , мы введем три простые переменные без индексов: Q, P, L, которые в цикле будут принимать соответствующие значения: , , ; , , ; 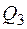, , и так далее. На каждом n-м шаге цикла эти величины будут вычисляться по формулам:

, ,

.

До начала цикла , . На каждом n-м шаге цикла проверяется условие . Если используется цикл с предусловием, то надо еще до цикла задать также начальное значение величины L. Это может быть любое большое число, например , чтобы условие окончания цикла не выполнилось случайно до выполнения первого шага.

Поскольку значение 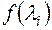используется после вычисления два раза, мы введем переменную , воспринимающую это значение. Это необходимо сделать, поскольку при повторном обращении к датчику случайных чисел мы получим уже другое случайное значение, а нам нужно, чтобы случайные значения функции в формулах для P и Q были одинаковыми.

Будем считать, что у нас есть датчик значений случайной величины, равномерно распределенной на . Обозначим через очередное случайное значение, выдаваемое этим датчиком. Тогда будет представлять собой значение случайной величины, равномерно распределенной на . Именно это значение мы будем использовать в качестве аргумента при вычислении случайных значений подынтегральной функции.

Запишем получившийся алгоритм на алгоритмическом языке:

алг Метод Монте-Карло (первая схема) (аргвещ a, b, , резвещ Q)

начвещ P, L, fr; цел n

| Вычисление первого

| случайного значения функции

; ; | Задание начальных значений

; | параметров.

нцпока L> | Начало цикла метода Монте-Карло.

; | Изменение значения параметра n.

| Вычисление очередного

| случайного значения функции

кц | Конец цикла метода Монте-Карло.

Кон

5. Составить алгоритм вычисления приближенного значения интеграла методом Монте-Карло (вторая схема), , для заданного n. Записать алгоритм на алгоритмическом языке.

Решение:

Исходными данными для алгоритма являются значения a, b, n, и функция . Приближенные значения интеграла вычисляются по формуле: . Здесь n – число испытаний (бросаний случайной точки , равномерно распределенной в прямоугольнике ), - мажорантная оценка функции на , - количество попаданий случайной точки в криволинейную трапецию, ограниченную сверху графиком функции при n испытаниях. Условие попадания точки в трапецию: .

Будем считать, что у нас есть датчик значений случайной величины, равномерно распределенной на . Обозначим через очередное случайное значение, выдаваемое этим датчиком. Тогда будет представлять собой значение случайной величины, равномерно распределенной на , а - значение случайной величины, равномерно распределенной на . А точка - значение случайной точки, равномерно распределенной в прямоугольнике .

Запишем алгоритм вычисления на алгоритмическом языке.

алг Метод Монте-Карло (вторая схема) (аргвещ a, b, , цел n, резвещ Q )

начвещ , , цел i, m

| Задание начального значения числа попаданий

нцдля i от 1 до n | Начало цикла подсчета числа

| попаданий

| Вычисление случайного значения

| абсциссы

| Вычисление случайного значения

| ординаты. Значения в этой строчке

| и в предыдущей должна быть разными.

| Это достигается повторным обращением

| к датчику случайных чисел

если

то

Все

кц | Конец цикла подсчета числа попаданий.

| Теперь .

Кон

6. Составить алгоритм вычисления приближенных значений первообразной в заданных точках , где 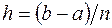- шаг сетки, . Приближенные значения первообразной во всех точках должны вычисляться спогрешностями, не превышающими заданного положительного числа . Для вычисления значений интегралов с заданной точностью использовать готовый алгоритм, построенный в примере 3.

Решение:

Исходными данными для алгоритма являются значения a, b, n, и функция . Приближенные значения первообразной в точках 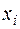вычисляются по схеме:

, , .

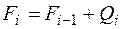Здесь 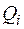- приближенные значения интегралов , вычисляемые с погрешностями, не превышающими . Для вычисления этих интегралов используем алгоритм из примера 3.

Запишем алгоритм на алгоритмическом языке.

алг Табулирование первообразной (аргвещ a, b, , цел n, резвещтаб )

начвещ x, h, Q, цел i

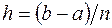| Вычисление шага сетки

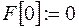| Задание начального значения первообразной

нцдля i от 1 до n | Начало цикла вычисления

| значений первообразной

| . При этом .

Метод Симпсона с автоматическим выбором шага (x-h, x, , Q)

кц | Конец цикла вычисления значений первообразной

Кон

7. Подготовить все необходимое для вычисления приближен-ного значения несобственного интеграла с погрешностью, не превышающей .

Решение:

Будем выбирать значение величины b исходя из требования:

.

Подынтегральная функция положительна, следовательно, и интеграл тоже, и модуль можно убрать. Кроме того,

.

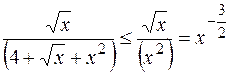Отсюда

Для определения значение величины b получается неравенство: . Решая его, получим: .

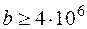Искомое приближенное значение несобственного интеграла представляет собой приближенное значение определенного интеграла

с погрешностью, не превышающей . Для его вычисления можно использовать любую квадратурную формулу.

8. Подготовить все необходимое для вычисления приближен-ного значения несобственного интеграла с погрешностью, не превышающей .

Решение:

Будем выбирать значение величины c 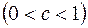исходя из требования:

.

Как известно, модуль интеграла не превышает интеграла от модуля:

.

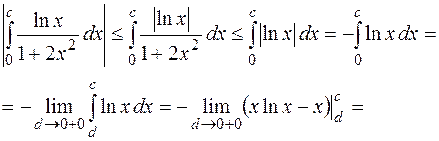
Здесь использовано, что

.

Для определения значения величины с получается неравенство: 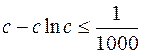. Решить это неравенство точно невозможно. Исследуем функцию . Найдем при . Следовательно, функция возрастает при . Кроме того, , а . Таким образом, наше неравенство решение имеет. Будем искать его подбором. Вычислим несколько значений этой функции при разных значениях с. Для этого можно использовать электронную таблицу Excel или систему программирования Паскаль. Желательно, чтобы искомое значение с было побольше. Таким путем подбирается по возможности наибольшее значение с, удовлетворяющее решаемому неравенству: с = 0,00009.

Искомое приближенное значение несобственного интеграла представляет собой приближенное значение определенного интеграла

с погрешностью, не превышающей . Для его вычисления можно использовать любую квадратурную формулу.

9. Составить алгоритм для вычисления приближенного значения двойного интеграла , где - область, ограниченная линиями: , , , 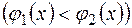. При построении кубатурной формулы использовать метод повторного интегрирования и метод средних прямоугольников. В алгоритме должно быть реализовано вычисление приближенного значения интеграла Q при заданном значении m. Записать алгоритм на алгоритмическом языке.

Решение:

Исходными данными для алгоритма являются значения a, b, m, функции , , . Вначале вычисляются и :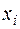

, , , .

Затем вычисляются :

, .

После этого вычисляются и :

, ,

, , .

Затем вычисляется приближенное значение интеграла :

.

С целью экономии оперативной памяти и в связи с тем, что значения m и заранее не известны, мы не будем вводить массивов. Обойдемся простыми переменными без индексов. Введем переменные xi, xxi, yij, yyij, ni, hyi, которые в соответствующих циклах будут принимать значения 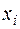, , , , , . Кроме того, введем переменную S для вычисления внутренней суммы.

Запишем алгоритм на алгоритмическом языке.

алг Вычисление двойного интеграла (аргвещ a, b, цел m,

резвещ Q)

начвещ xi, xxi, yij, yyij, hyi, S, , цел i, j, ni

:=(b-a)/m; Q:=0 | Вычисление шага сетки по оси x.

| Задание начального значения суммы

| (приближенного значения интеграла)

нцдля i от 1 до m | Начало цикла для вычисления

| внешней суммы.

xi:=a+ ; xxi:=xi- | , .

| .

| .

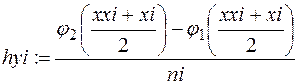S:=0 | Задание начального значения для внутренней

|суммы.

нцдля j от 1 до ni | Начало цикла для вычисления

| внутренней суммы.

, |

, |

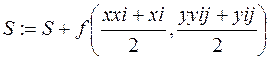
кц | Конец цикла для вычисления внутренней суммы

;

кц | Конец цикла для вычисления внешней суммы.

Кон