СИМФЕРОПОЛЬСКИЙ КОЛЛЕДЖ КИЕВСКОГО НАЦИОНАЛЬНОГО ЭКОНОМИЧЕСКОГО УНИВЕРСИТЕТА

Используя теоремы двойственности, можно, решив симплексным методом прямую задачу, найти оптимальное решение двойственной задачи. Метод одновременного решения пары взаимодвойственных задач заключается в следующем.

1. Обе задачи приводят к каноническому виду и устанавливают соответствие между переменными обеих задач.

2. Решают с помощью симплекс-метода ту из двух задач, где свободные члены в выражениях для базисных переменных неотрицательны (предполагается, что одна из задач таким свойством обладает).

3. На основании первой теоремы двойственности определяют оптимальное значение целевой функции второй задачи: или f_max = g_min.

4. На основании второй теоремы двойственности выписывают оптимальное решение второй задачи. Для этого целевую функцию первой задачи выражают через свободные, или неосновные, переменные. Тогда компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции прямой задачи, выраженной через неосновные переменные ее оптимального решения.

При использовании симплекс-таблиц из последней симплекс-таблицы выделяют последнюю строку, в которой числа, соответствующие переменным прямой задачи, присваивают компонентам оптимального решения двойственной задачи на основе соответствия переменных прямой и двойственной задачи.

Вернемся к примеру п. 4.3.

Прямая ЗЛП: Двойственная ЗЛП:

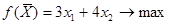
Канонический вид:

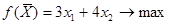
Установим соответствие между переменными двух задач:

Переменные прямой задачи I
Первоначальные	Дополнительные
х1 y4	х2 y5	х3 y1	х4 y2	х5 y3
Дополнительные	Первоначальные
Переменные двойственной задачи II

Первой решается прямая задача, поскольку для нее свободные члены в выражениях для базисных переменных неотрицательны:

х₃ = 4 – х₁ – 2х₂,

х₄ = 3 – х₁ – х₂,

х₅ = 8 – 2х₁ – х₂.

Итоговая симплекс-таблица решения прямой задачи имеет вид:

сi	БП
х1	х2	х3	х4	х5	bi
	x2				-1
	x1			-1
	x5				-3
Dj

Значение целевой функции двойственной задачи равно значению целевой функции прямой задачи: = = 10.

Оптимальное решение прямой задачи: 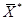= (2, 1, 0, 0, 3).

Оптимальное решение двойственной задачи: = (1, 2, 0, 0, 0), поскольку y₁ « x₃, y₂ « x₄, y₃ « x₅, y₄ « x₁, y₅ « x₂.

Последней симплекс-таблице соответствуют следующие уравнения для базисных переменных, входящих в целевую функцию:

х₁ – х₃ + 2х₄ = 2,

х₂ + х₃ – х₄ = 1.

Откуда

х₁ = 2 + х₃ – 2х₄,

х₂ = 1 – х₃ + х₄.

Выразим целевую функцию через свободные переменные:

= 3×(2 + х₃ – 2х₄) + 4×(1 – х₃ + х₄) = 10 – х₃ – 2х₄.

Таким образом, в соответствии со второй теоремой двойственности y₁ = 1, y₂ = 2, значения остальных переменных оптимального решения двойственной задачи y₃, y₄, y₅ равны нулю, поскольку они не входят в выражение целевой функции.

Следует отметить, что положительным (ненулевым) компонентам оптимального решения одной из взаимодвойственных задач соответствуют нулевые компоненты оптимального решения другой задачи:

Переменные прямой задачи I
Первоначальные	Дополнительные
Дополнительные	Первоначальные
Переменные двойственной задачи II

Такое соответствие было отмечено в рассмотренной ранее теореме.

[1] Орлов А.И. Теория принятия решений: учебник / А.И. Орлов. – М.: Издательство «Экзамен», 2006. – С. 15 -18.

[2] Замков. О.О. Математические методы в экономике: учебник / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных. – М. : МГУ им. М.В. Ломоносова, Издательство «ДИС», 1997. – С. 13 – 14.

[3] Моисеев Н.Н. Математические задачи системного анализа. М.: Наука, 1981. 488 с.

[4] Материал лекции подготовлен на основе учебного пособия: Воронин А.А., Губко М.В., Мишин С.П , Новиков Д.А. Математические модели организаций: Учебное пособие. — М.: ЛЕНАНД, 2008. — 360 с.

[5] Моисеев Н.Н. Прощание с простотой. – М.: АГРАФ, 1998.

[6] Новиков А.М., Новиков Д.А. Методология. – М.: Синтег, 2007.

[7] Волкова В.Н., Денисов А.А. Основы теории систем и системного анализа. Изд. 2-е. – СПб.: СПб.ГТУ, 1999.

[8] Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики: учеб. пособие. 2-е изд., доп. – СПб.: Питер, 2010. – С. 16–17.

[9] Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики: учеб. пособие. 2-е изд., доп. – СПб.: Питер, 2010. – С. 17 – 18.

[10] Орлова И.В., Половников В.А. Экономико-математические методы и модели: компьютерное моделирование: Учеб. пособие. – М.: Вузовские учебник, 2009. – С. 54 – 55.

[11] Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики: учеб. пособие. 2-е изд., доп. – СПб.: Питер, 2010. – С. 18.

[12] Там же. С. 57 – 58.

[13] Там же. С. 59.

[14] Там же. С. 59 – 60.

[15] Косоруков О.А., Мищенко А.В. Исследование операций: учебник / О.А. Косоруков, А.В. Мищенко; под общ. ред. д. э. н., проф. Н.П. Тихомирова. – М.: Изд-во «Экзамен», 2003. – С. 19–20.

[16] Михайлова Э.А., Смирнов А.О. Методы нахождения оптимального управления экономическими системами: пособие для практических занятий / РГАТА. Кафедра экономики. - Рыбинск, 1998. - 42 с.

[17] Красс М.С., Чупрынов Б.П. Математические методы и модели для магистрантов экономики: учеб. пособие. 2-е изд., доп. – СПб.: Питер, 2010. – С. 30-32.

[18] Там же. С. 33 – 35.

[19] Там же. С. 35- 36.

[20] Там же. С. 36- 37.

СИМФЕРОПОЛЬСКИЙ КОЛЛЕДЖ КИЕВСКОГО НАЦИОНАЛЬНОГО ЭКОНОМИЧЕСКОГО УНИВЕРСИТЕТА