Частотное распределение случайного спроса

Разобьем весь диапазон изменения спроса (в нашей выборке спрос заключен в пределах от 0 до 2-х контейнеров) на небольшое число более мелких интервалов так, чтобы в каждый из них попали какие-то точки из нашей выборки (Рис. 201 а). Подсчитаем количество точек выборки, попавших в каждый такой интервал и построим диаграмму частотного распределения спроса (Рис. 201 б).

Площадь каждого из прямоугольников на этой диаграмме равна доли точек, попадающих в интервал, на который такой прямоугольник опирается (Рис. 201 б). Очевидно, что сумма площадей всех прямоугольников на диаграмме частотного распределения равна 1.

Рис. 201

Частотное распределение дает оценку вероятности попадания спроса в каждый из выделенных интервалов. С его помощью можно попытаться оценить риск дефицита. Представим себе, что мы планируем запас товара на один день, зная, что средний спрос равен 1 контейнеру. Допустим, что мы собираемся оставить на один день торговли 1,2 контейнера данного товара. Какова будет вероятность того, что спрос превысит наш запас, и возникнет дефицит?

Для ответа на этот вопрос попробуем просто сложить площади прямоугольников, опирающихся на интервалы [1,2-1,4], [1,4-1,6], [1,6-1,8] и [1,8-2,0] (Рис. 201 б). Площадь каждого из прямоугольников равна частоте, с которой спрос из нашей выборки попадал в каждый из этих интервалов. Сумма площадей этих прямоугольников, очевидно, покажет, как часто спрос превышал 1,2 контейнера. В данном случае окажется, что это частота равна 0,22 (22 точки из 100 вошедших в выборку лежат выше ординаты 1,2).

Если эту частоту, которая относится к случайной выборке из истории продаж данного товара использовать, как оценку вероятности того, что спроспревысит 1,2 контейнера, то получается, что вопрос об оценки риска возникновения дефицита решен.

Однако, на самом деле, оценка вероятности по частоте всегда сопряжена с ошибкой, которая тем больше, чем меньше размер выборки. Если мы подбрасываем монету 10 раз, то вполне возможно, что орел выпадет 8 раз, что приведет к оценке выпадения монетки на орла равной 0,8. Разумеется, если подбросить монету 100 раз, выпадение орла 80 раз практически исключено, и оценка вероятности получится гораздо более близкой к 0,5. Статистика позволяет оценить ошибки в оценках вероятности по частоте и среднего и стандартного отклонения по выборке [1]. Допустим, в нашем случае выборки из 100 чисел – значений спроса на некоторый товар за предшествующие 100 дней, среднее значение оценено как 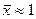, а стандартное отклонение спроса – как . Тогда стандартная ошибка 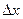в определении среднего составит

где N=100 – размер выборки. Такого же порядка будет и ошибка в определении стандартного отклонения s (хотя формула для нее будет сложнее). А вот относительная стандартная ошибка в определении вероятности p попадания случайного спроса в тот или иной интервал частотной диаграммы будет равна

что для p»0,1 и N = 100 составит величину в 30%, а для p»0,01 – почти 100%! Разумеется, увеличение размера выборки позволяет уменьшить и ошибки в оценке распределения вероятностей, однако, на практике в бизнесе редко удается получить большие выборки. Кроме того, если, как в случае, показанном на Рис. 200, среднее (ожидаемое) значение спроса меняется со временем, получение адекватного частотного распределения существенно усложняется.

Вместе с тем, оказывается, что во многих случаях специальных исследований для оценки распределения вероятностей интересующей нас величины (в частности, распределения вероятностей различных значений спроса) по частотному распределению выборочных значений не требуется. Дело в том, что если нас интересует суммарный спрос за несколько (L) дней или суммарный спрос в нескольких сравнимых друг с другом торговых точек, то его распределение заранее известно.

Независимо от того, как распределено каждое случайное слагаемое в сумме случайных величин, сама сумма должна быть распределена нормально со средним значением, равным сумме средних значений слагаемых (формула 4) и дисперсией, равной сумме дисперсий слагаемых (формула 5).

Это утверждение выражает важнейший статистический закон, известный как центральная предельная теорема теории вероятностей [2]. Везде, где мы имеем дело с суммой случайных величин (не важно, одинаково распределенных или нет, если только одна или несколько из них не доминируют над всеми остальными), мы встречаем это замечательное распределение вероятностей. Даже если речь идет о спросе за 1 день, он весьма часто формируется благодаря множеству малых случайных факторов, и потому также распределен нормально.

Это распределение очень часто встречается на практике и в других случаях (именно поэтому оно и называется нормальным). Вследствие этого стоит изучить его свойства и использовать для оценки различных рисков, в частности, риска возникновения дефицита.