КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЛЕКЦИЯ № 3
Метод Гаусса с выбором главного элемента
(оптимальный метод).
Пусть имеется система уравнений, записанная в виде (1).
Выберем в первом уравнении максимальный по модулю ненулевой элемент.
Пусть, например, элемент,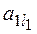 
, стоящий в 
столбце матрицы А. Разделим первое уравнение системы на 
, который будем называть ведущим элементом первого шага. В результате получим новое эквивалентное уравнение:
(2)
где
Исключим с помощью уравнения (2) 
из всех остальных уравнений
системы (1). Для этого
1. будем умножать уравнение (2) на 
2. вычитать из i-того уравнения системы.
Полученная эквивалентная система уравнений будет иметь вид: 
(3)
Где
В частности получается
На втором шаге выбираем во втором уравнении максимальный по модулю элемент.
Пусть это будет, например, 
,
1. делим второе уравнение (3) на .
2. Получившееся новое второе уравнение, умножаем на 
3. и вычитаем из i -того уравнения системы (3), для всех i¹ 2.
В итоге после второго шага получим следующую систему, эквивалентную системе (3):
Где
На k -ом шаге в k -том уравнении
1. выбираем максимальный по модулю ненулевой элемент 
.
2. Делим k -ое уравнение на этот элемент.
3. Получившееся уравнение умножаем на 
4. и вычитаем из всех оставшихся уравнений при i¹k .
Продолжая этот процесс, придем к одному из следующих случаев:
1. Система, если опустить нули, будет иметь вид:
(4)
В этом случае система определенная, имеет единственное решение, которое фактически уже записано в виде (4).
2. На каком то шаге получим уравнение вида:
В этом случае система несовместна, т.е. не имеет решений.
3. На каком то шаге получится уравнение 0=0.
В этом случае данное уравнение надо исключить из рассмотрения, т.к. оно оказалось линейной комбинацией остальных уравнений системы.
Продолжая далее вычисления, мы придем либо к случаю 2), либо получим систему:
Система имеет множество решений.
Переменные
- базисные; 
- свободные.
Начинать решение системы по методу оптимального исключения можно не с первого уравнения, а с произвольного.
За ведущий элемент на первом шаге можно выбрать максимальный элемент матрицы системы.
На очередном k -ом шаге за ведущий элемент можно брать максимальный ненулевой элемент из всех элементов матрицы системы, исключая элементы тех строк, в которых уже выбирались ведущие элементы на предыдущих шагах.
При таком способе проведения вычислений естественно ожидать, что погрешности вычислений будут невелики, т.к. всегда делятся меньшие числа на большие числа.
Проводя же вычисления, например, по методу Гаусса, приходится иногда делить большие числа на меньшие. При этом погрешность результата деления может получиться очень большой.
Применения метода Гаусса к вычислению определителей и обратных матриц.
Дата добавления: 2014-12-03; просмотров: 86; Мы поможем в написании вашей работы!; Нарушение авторских прав |