с) Пара вращений.

Вращения направлены в разные стороны, но . Такая совокупность вращений называется парой вращений.

М.Ц.С. – находится в бесконечности и все точки будут иметь одинаковые скорости, следовательно результирующее движение будет поступательным.

3. Сложение вращений вокруг пересекающихся осей.

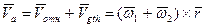
, где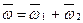

Если векторы мгновенных угловых скоростей слагаемых движений пересекаются, то они складываются по правилу параллелограмма.

Мгновенное результирующее движение – есть вращение вокруг мгновенной оси, проходящей через т. О.

4. Сложение поступательного и вращательного движений.

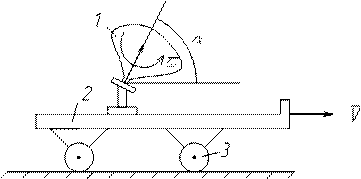
V – скорость переносного движения для тела 1 – относительное движение вращение с угловой скоростью , для тела 3 – относительное движение вращение вокруг его оси.

а) Случай когда скорость поступательного движения перпендикулярна к оси вращения ( )

Это плоскопараллельное движение

А – полюс, то рассматриваемое движение будет слагаться из поступательного со скоростью и из вращательного вокруг оси Аа. Проходящей через полюс.

,

a AP найдем из равенства

Мы получим, что движение тела в этом случае можно рассматривать как мгновенное вращение вокруг оси Рр, т.е. точка Р является м.ц.с.

б) Винтовое движение ( )

Аа – ось винта правый винт

h – шаг винта

Т – время одного оборота

VT=h и 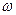T=2 T= ; h= ;

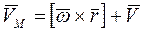
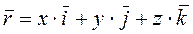
, где

в) Скорость поступательного движения образует произвольный угол с осью вращения,(общий случай свободного твердого тела)

- V’’ заменим парой ,

АС= , тогда у тела остается вращение с угловой скоростью и поступательное движение со скоростью ,т.е. распределение скоростей точек тела будет таким же как при винтовом движении вокруг оси Сс с угловой скоростью и поступательной скоростью

Сс – называют мгновенной винтовой осью.

Таким образом, движение свободного твердого тела можно рассматривать как слагающиеся из серии мгновенных винтовых осей.

Пример 2

Коническая шестерня (бегунок) обегает горизонтально расположенную шестерню n=150 раз в минуту. Радиус опорной шестерни R=20 см, а угол раствора конуса бегунка . Определить угловую скорость качения бегунка по опорной шестерне. Скорость точки B бегунка и ускорение точки C бегунка.

Решение:

Скорость точки C бегунка равна нулю, т.к

OC - мгновенная ось вращения

AO – ось относительного вращения

из параллерограмма скоростей найдем

Определению ускорений точек бегунка должно предшествовать вычисление углового ускорения бегунка в его абсолютном движении

Конец вектора - точки K описывает в горизонтальной плоскости окружность радиусом . Это и будет годогроф вектора угловой скорости. Сам вектор вращается вокруг вертикальной оси с угловой скоростью . Угловое ускорение бегунка равно скорости движения точки K годогрофа угловой скорости

И направлено из точки О перпендикулярно плоскости чертежа.

, т.к

И направлено ускорение точки С по правилу правого винта.