Диференціальне рівняння вимушених коливань і його розв’язування

Щоб у реальній коливальній системі одержати незатухаючі коливання, треба компенсувати цій системі втрати енергії. Таку компенсацію можна здійснити за допомогою якого-небудь періодично діючого фактора X(t), який змінюється за гармонічним законом:

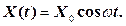
Для механічних коливань пружинного маятника роль X(t) відіграє зовнішня вимушуючи сила

(1)

З урахуванням цієї сили закон руху пружинного маятника запишеться у вигляді

Якщо скористатися позначеннями , , то прийдемо до рівняння

(2)

Рівняння (2) є неоднорідним лінійним диференціальним рівнянням другого порядку. Розв’язок такого рівняння складається з двох частин, загального розв’язку відповідного рівняння без правої сторони і часткового розв’язку цього рівняння з правою стороною, тобто

де A₀ ─ амплітуда зміщення в початковий момент часу (t=0); А ─ амплі-туда коливань, яка установиться через деякий час.

Через деякий час t₁, завдяки дії вимушеної сили F₀ , амплітуда коливань досягне максимального значення (рис. 1). З цього моменту часу розв’язком рівняння (2) буде лише функція

(3)

Рис. 1

Відповідні похідні від (3) підставимо в рівняння (2), одержимо

(4)

У виразі (4) сталі величини А і ω повинні мати такі значення, щоб гармонічна функція 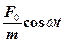дорівнювала сумі трьох гармонічних функцій, які стоять в лівій частині рівняння. Для виконання цієї умови, необхідно щоб сума трьох векторів при відповідних косинусах в лівій частині (4) дорівнювала вектору, який стоїть біля косинуса в правій частині. Однак вектори і напрямлені по одній лінії, але в різні боки. Вектор 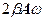напрямлений перпендикулярно до перших двох. Зазначена вище умова може бути реалізована за допомогою векторної діаграми (рис. 2).

Векторна діаграма дає можливість визначити амплітуду і початкову фазу вимушених коливань. З діаграми видно, що

. (5)

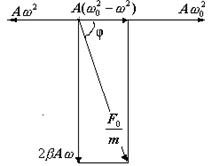
Рис. 2

Звідки амплітуда вимушених коливань буде дорівнювати

(6)

Початкова фаза вимушених коливань, як видно з векторної діаграми, дорівнює

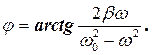(7)

З урахуванням співвідношень (6) і (7) розв’язок диференціального рівняння вимушених коливань (2) матиме вигляд

(8)

Якщо розглянути електричний коливальний контур, то роль змінної величини в цьому випадку буде мати е.р.с., або змінна напруга

(9)

Диференціальне рівняння вимушених коливань в коливальному контурі, з урахуванням (9), буде мати вигляд

(10)

Використовуючи позначення, аналогічні до (2), прийдемо до рівняння

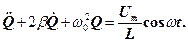(11)

Розв’язком рівняння (11) є функція, аналогічна до (3), тобто

(12)

Амплітуда заряду вимушених електромагнетних коливань буде дорівнювати

. (13)

Підстановка значень і в (13) дає значення амплітуди електромагнетних коливань в такому вигляді

(14)

Похідна за часом від (12) дає можливість одержати в коливальному контурі закон зміни електричного струму

,

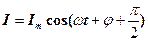де ─ максимальний струм у коливальному контурі.