Гармонічні коливання. Диференціальне рівняння гармонічних коливань та його розв’язок. Амплітуда, фаза, частота, період коливань

Коливаннями називають процеси, які повторюються з певною періодичністю. В залежності від механізму виникнення коливань розглядають механічні, електромагнітні, електромеханічні і т. п. коливання, а в залежності від характеру сил, що діють на коливну систему, – вільні (власні), згасаючі, вимушені тощо.

Розгляд почнемо з власних механічних коливань горизонтального пружинного маятника, який складається з тіла масою m, закріпленого до кінця пружини, що жорстко прикріплена до стінки (рис. 5.1).

Якщо вивести тіло з положення рівноваги, то на нього почне діяти повертаюча сила пружної деформації пружини, яка задається законом Гука . Якщо знехтувати тертям і масою пружини у порівнянні з масою тіла, то при невеликих деформаціях пружини закон руху – ІІ закон Ньютона – запишеться як

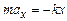, (5.1)

де k – коефіцієнт пружності (жорсткість пружини), х – зміщення тіла від положення рівноваги, а_х – прискорення вздовж осі Х. В подальшому всяку силу, пропорційну до зміщення і напрямлену до положення рівноваги, будемо називати квазіпружною, незалежно від її природи.

Оскільки прискорення 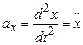, то (5.1) можна переписати як

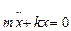
або

. (5.2)

У рівнянні (5.2) 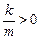, тому можна ввести позначення

, (5.3)

де називають власною циклічною частотою коливань.

Підставляючи (5.3) у (5.2), одержимо диференціальне рівняння коливань не тільки пружинного маятника, але усякого тіла (матеріальної точки), на яке діє квазіпружна сила:

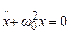. (5.4)

Легко показати, що розв’язком цього рівняння є гармонічні функції (рис. 5.2)

або 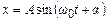. (5.5)

Коливання, в яких зміна фізичної величини в залежності від часу відбувається за законом синуса або косинуса, називаються гармонічними. В (5.5): А – амплітуда коливань – найбільше значення коливної фізичної величини (у даному випадку, максимальне зміщення від положення рівноваги), 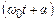– фаза коливань, a – початкова фаза.

Проміжок часу, протягом якого здійснюється одне повне коливання, називається періодом коливань Т. Зрозуміло, що 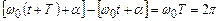, оскільки гармонічні функції повторюються через 2p. Звідси циклічна частота

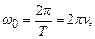(5.6)

де 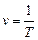– лінійна частота, як кількість коливань, здійснених за одиницю часу.

Для пружинного маятника 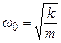, тому період коливань

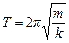. (5.7)