Ядерна модель атома. Борівський воднеподібний атом. Спектральні серії

7.1.1. Оскільки світло випромінюється і поглинається атомами речовини, то виникає питання: яка структура атомів забезпечує дискретний (квантовий) характер вказаних процесів? Вперше конструктивну відповідь на це питання дав Резерфорд (1911р), досліджуючи розсіяння 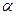-частинок на тонких (товщина » 1 мкм) металічних плівках (фольгах) (рис.7.1).

Центрований діафрагмою 2 пучок a-частинок від джерела 1 розсіювався фольгою 3 під різними кутами J від -p до p. Кількість a-частинок (Dn), розсіяних під фіксованими кутами, реєструвалась приймачем 4, який міг переміщуватись по колу навколо центру фольги. Було встановлено (рис.7.2):

а) більшість a-частинок, проходячи через фольгу, практично не розсіюється;

б) дуже добре виконується теоретично передбачуване співвідношення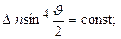

в) певна, хоч і незначна, кількість a-частинок розсіюється під кутами, близькими до ±p.

Аналіз результатів експерименту дозволив Резерфорду запропонувати ядерну модель атома, згідно з якою в центрі атома 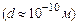розміщене позитивно заряджене ядро 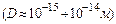, що володіє масою, приблизно рівною масі атома. Навколо ядра рухаються електрони. Якщо в нейтральному атомі Z електронів, де Z – порядковий номер елементу в періодичній таблиці елементів Д.І. Менделєєва, то заряд ядра 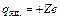, де 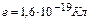– елементарний заряд. В рамках цієї моделі зрозуміло, що ймовірність лобового зіткнення a-частинки з ядром, яке забезпечує розсіяння на кути ±p, дуже мала. Електрони ж в силу незначної маси розсіювати a-частинки не можуть.

Оскільки, у відповідності з теоремою Ірншоу, неможлива стійка статична конфігурація електричних зарядів, то атом мусить бути динамічною системою, тобто електрони повинні рухатись навколо ядра по замкнених (колових чи еліптичних) орбітах. Такий рух є прискореним, і електрон з точки зору класичної фізики повинен втрачати енергію, випромінюючи електромагнітні хвилі, і тому впасти на ядро. Але, як відомо, атом – стійка конфігурація електричних зарядів. І тому, приймаючи ядерну модель атома, потрібно відмовитись від класичного опису орбітального руху електронів.

7.1.2. Розвиваючи запропоновану модель, у 1913 р. Н. Бор висунув гіпотезу у вигляді наступних постулатів: а) із усіх можливих механічних станів (орбіт) електрона в атомі здійснюються лише такі, для яких момент імпульсу орбітального руху електрона кратний до постійної Планка h, тобто

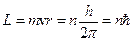, (7.1)

де 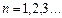– квантове число стану (номер орбіти), а 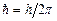– постійна Дірака; такі стани називаються стаціонарними;

б) перебуваючи в стаціонарному стані, електрон атома не випромінює і не поглинає енергії;

в) при переході з одного стаціонарного стану на інший електрон випромінює чи поглинає квант світла з енергією, рівною різниці енергій цих станів, тобто

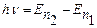. (7.2)

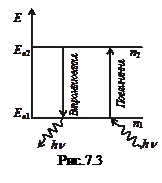
Отже, основна ідея постулатів Бора полягає в квантуванні (дискретності) механічних характеристик руху електронів: моменту імпульсу, енергії тощо. Рис.7.3 ілюструє наявність стаціонарних квантових станів (енергетичних рівнів) з енергіями 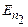та 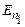і випромінювальні та поглинальні переходи між ними: зменшення енергії електрона супроводжується випромінюванням кванту світла (фотона) з енергією 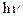; поглинання кванту світла з енергією 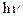забезпечує збільшення енергії електрона від 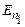до 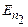. В цій моделі випромінювання (поглинання) квантів світла з енергіями 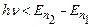є неможливим.

7.1.3. Запропонована теорія вперше була застосована до воднеподібних атомів ( 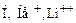тощо), в яких навколо ядра, заряд якого 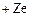, рухається по коловій орбіті радіусом r лише один електрон. При цьому ядро вважається нерухомим. Розглядаючи електрон як класичну матеріальну точку, енергію атома запишемо як суму кінетичної і потенціальної енергій електрона в кулонівському полі ядра

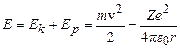, (7.3)

де m – маса електрона, 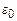– електрична стала. Врахуємо, що в ролі доцентрової сили, яка забезпечує коловий рух електрона, виступає кулонівська сила, тобто

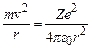. (7.4)

Звідси випливає, що 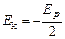, і (7.3) запишеться у вигляді

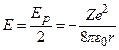. (7.5)

Оскільки орбітальний момент імпульсу електрона

,

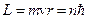то, врахувавши (7.4), отримаємо вираз для радіуса стаціонарної орбіти електрона

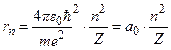, (7.6)

де має зміст радіуса першої (n = 1) орбіти електрона в атомі водню (Z = 1); ця величина називається борівським радіусом. Отже, має місце квантування (n = 1, 2, 3, …) радіусів стаціонарних орбіт електрона.

Підставляючи (7.6) у (7.5), отримаємо вираз для енергії атома

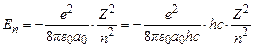. (7.7)

Введемо позначення: – постійна Рідберга. Тоді (7.7) набуде остаточного вигляду

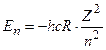. (7.8)

Отже, енергія атома приймає дискретні значення, тобто квантується. Стан з найнижчою енергією (n = 1) називається основним, усі інші стани – збудженими. Стан з найвищою енергією (n = ¥) відповідає іонізації атома. Отже, енергія іонізації воднеподібних атомів

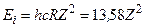, (еВ).

І тому зручно інколи (7.8) записувати у вигляді

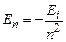. (7.9)

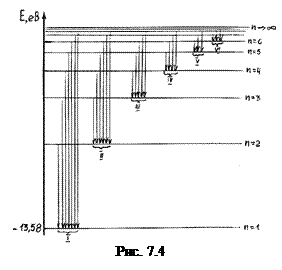
7.1.4.Зобразимо енергетичну діаграму атома водню (Z = 1) (рис.7.4). В основному стані атом може перебувати як завгодно довго. Якщо ж його перевести певним чином (теплом, світлом, бомбардуванням вільними електронами тощо) в довільний збуджений стан, то тривалість перебування в цьому стані складає 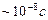, і атом самовільно переходить в основний чи нижчі збуджені стани, як показано на рис. 7.4. При цьому, у відповідності з (7.2) та (7.8), випромінюється фотон з енергією

,

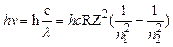а довжина випромінюваної світлової хвилі розраховується за серіальною формулою Бальмера

, (7.10)

де n₂ – квантове число стану, з якого відбувається перехід, n₁ – квантове число стану, в який переходить атом.

Якщо забезпечити умови “заселеності” усіх збуджених станів, то в спектрі випромінювання атомарного водню спостерігатиметься значна кількість спектральних ліній, які можна згрупувати в наступні серії:

І–серія Лаймана, для якої а ;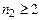

ІІ–серія Бальмера, для якої 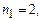а ;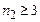

ІІІ–серія Пашена, для якої а ;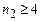

ІV–серії Брекета, для якої а 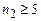, тощо.

Лінії серії Лаймана лежать в ультрафіолетовій області, серії Бальмера – у видимій області, серії Пашена, Брекета – в інфрачервоній області. Відмітимо, що довжини хвиль, розраховані за формулою (7.10), дуже добре співпадають з експериментальними значеннями.

На цьому тріумф теорії Бора закінчується, бо вона виявилась нездатною пояснити спектри випромінювання складних (неводнеподібних) атомів, а також інтенсивності спектральних ліній навіть атомарного водню. Слабкість цієї теорії полягає в тому, що, ввівши нехарактерні для класичної фізики поняття про квантування фізичних величин і про квантові переходи (”стрибки”), в усьому іншому вона залишилась класичною. І тому послідовна, квантовомеханічна теорія повинна ґрунтуватись на нових (некласичних) принципах опису стану і руху мікрочастинок.