КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Якщо то ; проте , тобто , оскільки , то . Звідси або .
5. Матриця 
є ідемпотентною, rgA = 1 і матриця Z має таку властивість, що ( 
) — квадратна симетрична невироджена матриця.
Приклад 5. Нехай 
; тоді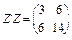 
;
,
отже, матриця 
— невироджена.
.
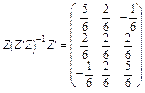Визначимо нову матрицю А так:
.
Матриця А — симетрична та ідемпотентна, оскільки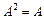 
. Зауважимо, що ранг матриці А дорівнює 1.
Знайшовши характеристичні корені цієї матриці, тобто розв’язавши рівняння 
, дістанемо 
= 1 і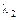 
= 0 кратності 2, що ілюструє виконання властивості 4.
Диференціювання функції багатьох змінних
(градієнт функціі f (x) )
Розглянемо операцію диференціювання функції багатьох змінних f (x1,x2 ... xn), коли змінні задано у формі матриці-рядка, або, що те саме, вектора, тобто X = (x1, x2 ... xn 
. Тоді можна коротко записати f (x) = (x1, x2 ... xn .
Означення 5. Градієнтом функції f(x) (позначається: 
) називається вектор, який складається з частинних похідних функції f (x) за x1, x2 ... xn:
(20)
Нехай потрібно визначити градієнт функції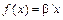 
, коли 
і 
.
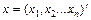Тоді
.
Отже, градієнт функції
. (21)
Узявши до уваги, що 
, градієнт можна визначити як
. (22)
Далі розглянемо функцію 
, де A = (aij) — симетрична матриця порядку n і 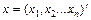— n-вимірна матриця-стовпець. Функцію такого типу визначають як квадратичну форму.
Визначимо градієнт квадратичної форми. Для цього подамо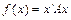 
як скалярний добуток:
(23)
.
Знайдемо компоненти вектора-градієнта.
Перший компонент
.
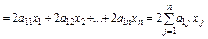другий компонент:
n-й компонент:
Отже, градієнт від квадратичної форми має вигляд
(24)
Отже, скорочено
(25)
Питання для самоконтролю.
1. Задані матриці:
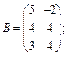
Знайдіть матриці суми (різниці):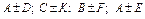 
. Поясніть, чому не існує суми (різниці) матриць: 
.
2. Для матриць із завдання 1 знайдіть добутки: BA; CF; CK; AE; DE. Поясніть, чому не існує добутків AB; CD; FC; FB; KA; KE.
3. Для матриць із завдання 1 знайдіть транспоновані до них матриці.
4. Із множини матриць завдання 1 знайдіть симетричні. Яка ознака симетричної матриці?
5. Покажіть, що для матриць із завдання 1 справджується тотожність 
.
6. Яка матриця називається ідемпотентною? Покажіть, що матриця 
є ідемпотентною.
7. Назвіть скалярні характеристики матриць.
8. Покажіть, що для матриць А і С із завдання 1 
; 
.
9. Дано матрицю 
. Чому дорівнює слід (tr A) матриці А?
10. Для матриці А із завдання 9 покажіть, що 
.
11. Дано симетричну матрицю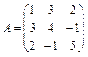 
. Покажіть, що 
.
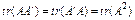12. Знайдіть визначник матриці А із завдання 11.
13. Для матриці А із завдання 11 покажіть, що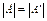 
.
14. Яка матриця має обернену матрицю? Які з поданих далі матриць мають обернені:
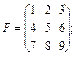
15. Наведіть основні властивості оберненої матриці.
16. Задано матрицю 
, обернену до матриці А:
.
Покажіть, що 
.
17. Покажіть, що матриця
.
є ортогональною.
18. Задана систему лінійних рівнянь
Матриця, обернена до матриці системи,
.
Знайдіть розв’язок даної системи рівнянь.
19. Яка матриця називається блоковою?
20. Задано по чотири блоки блокових матриць А і В:
; 
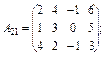
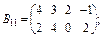
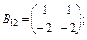
Знайдіть суму (різницю) блокових матриць 
.
21. Яка умова множення блокових матриць? З відповідних блоків матриць А і В з попереднього завдання складіть дві матриці, які можна було б помножити одна на одну.
22. Задано матриці
Знайдіть матрицю Кронеккeр-добутку (прямого множення) 
.
23. Задана блочна невироджена матриця
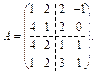
Знайдіть обернену матрицю .
24. Яке рівняння називають характеристичним рівняння матриці А?
25. Яку назву мають корені характеристичного рівняння?
26. Чому дорівнює добуток 
, де Х — власні вектори матриці А?
27. Знайдіть характеристичні корені і власні вектори матриці:
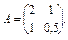
28. Дайте означення квадратичної форми. Запишіть її у розгорнутому вигляді і в матричній формі.
29. Коли квадратична форма є додатно визначеною і напіввизначеною?
30. Яку квадратичну форму називають випадковою квадратичною формою?
31. Чому дорівнює математичне сподівання випадкової квадратичної форми?
32. Сформулюйте властивості випадкової квадратичної форми.
Дата добавления: 2014-12-03; просмотров: 136; Мы поможем в написании вашей работы!; Нарушение авторских прав |