Проста модель експоційного згладжування.

Новий прогноз= αх (фактичний результат в останньому періоді) + (1-α)х (прогноз в останньому періоді), тобто F_t+1= αA_t + (1-α)F_t.

Константу згладжування α дослідник вибирає з відрізка (0,1). В умовах стабільності частіше αє (0,2;0,4).

Модель експоційного згладжування з поправкою на тренд.

Будуємо прогноз методом простого згладжування, а потім корегуємо його з поправкою на тренд за допомогою формули:

Прогноз з урахуванням тренда FIT_t = прогноз F_t + тренд T_t.

Тренд Т_t = (1-b)T_t-1 + b(F_t – F_t-1), де T_t і T_t-1 - загладжуваний тренд в періоди t і (t-1) , b - константа згладжування.

Питання для самоконтролю.

1. Дайте означення тимчасового ряду.

2. Назвіть фактори які формують значення тимчасового ряду.

3. Що таке тренд?

4. Що таке циклічне коливання тимчасового ряду?

5. Що таке випадкові фактори?

6. Адитивна модель тимчасового ряду.

7. Мультиплікативна модель тимчасового ряду.

8. Назвіть основні кроки побудови тимчасового ряду.

9. Що таке автокореляція?

10. Сформулюйте критерій Дарбіні-Уотсона.

11. Проста модель експоційного згладжування.

12. Модель експоційного згладжування з поправкою на тренд. T_t

Тема 4. Модель множинної регресії

Лекція 6

Тема лекції. Багатомірна лінійна модель.

Мета: ознайомити студентів з загальними принципами побудови багатомірної лінійної економетричної моделі

План лекції

1. Передумови застосування методу найменших квадратів

(1 МНК).

2. Оцінка параметрів рівняння множинної регресії.

3. Множинний коефіцієнт кореляції і детермінації.

4. Частинні коефіцієнти кореляції і коефіцієнти регресії.

5. F i t – критерії.

Література:

1. Наконечний С.І., Терещенко Т.О., Романюк Т.П. Економетрія: Навчальний посібник. – К.: КНЕУ,1998. – 351с.

2. Лук’яненко І. Г. Економетрика: Підручник / І. Г. Лук’яненко, Л. І. Краснікова. - К.: Товариство „Знання”, КОО, 1998. - 494 с.

3. Магнус Я. Р. Эконометрика. Начальный курс / Я. Р. Магнус, П. К. Катышев, А. А. Пересецький. –М.: Дело,1997. – 248 с.

4. Зацеркляний М.М. Вступ в економетрію: Навчальний посібник./М.М. Зацеркляний, І.І. Парфьонова. - Харків :ППФ “АЛМАКС”,2005. – 244 с.

5. Ершов С.Г. Использование пакета STATISTIKA для обработки данных: Учебно – практическое пособие/С.Г. Ершов. - Харьков: ХНЭУ, 2005. – 84 с.

Передумови застосування методу найменших квадратів

МНК).

Множинна регресія - рівняння зв'язку з декількома незалежними змінними:

y=f(x₁,x₂,…,x_m),
де у – залежна змінна (результативна ознака);

x₁,x₂,…,x_m - незалежні змінні (фактори).

Множинна регресія застосовується в ситуаціях, коли з безлічі факторів, що впливають на результативну ознаку, не можна виділити один домінуючий фактор і необхідно враховувати вплив декількох факторів.

Основна мета множинної регресії - побудувати модель з великим числом факторів, визначивши при цьому вплив кожного з них окремо, а також сукупний їх вплив на модельований показник.

Як і у випадку парної регресії, побудова рівняння множинної регресії здійснюється у два етапи
- специфікація моделі;
- оцінка параметрів вибраної моделі.
Включення в рівняння множинної регресії того чи іншого набору факторів пов'язано, перш за все, з поданням дослідника про природу взаємозв'язку модельованого показника з іншими економічними явищами.

Фактори, що включаються у множинну регресію, повинні відповідати наступним вимогам:
1. Вони повинні бути кількісно виміряні.
2. Фактори не повинні бути взаємно корельовані і тим більше знаходитися в точній функціональній залежності. Якщо між факторами існує висока кореляція, то не можна визначити їх ізольований вплив на результативний показник.

Включені у множинну регресію фактори повинні пояснити варіацію незалежної змінної. Якщо будується модель з набором m факторів, то для неї розраховується показник детермінації R², який фіксує частку поясненої варіації результативної ознаки за рахунок розглянутих у регресії m факторів.

Вплив інших, не врахованих у моделі, факторів оцінюється як 1-R² з відповідною залишкової дисперсією S².

При додатковому включенні в регресію (m+1) – фактора х_m+1 коефіцієнт детермінації повинен зростати, а залишкова дисперсія зменшиться , тобто

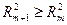та .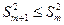

Якщо цього не відбувається і дані показники мало відрізняються один від одного, то включений в аналіз фактор х_m+1 не покращує модель і практично є зайвим чинником.

Насичення моделі зайвими факторами не тільки не знижує величину залишкової дисперсії і не збільшує показник детермінації, але призводить до статистичної незначущості параметрів регресії за t-критерієм Стьюдента.

Нехай економетрична модель у матричній формі має вигляд

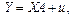(1)

де Y — вектор значень залежної змінної;

X — матриця незалежних змінних розміром 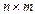(n — число спостережень, m — кількість незалежних змінних);

A — вектор оцінок параметрів моделі;*

u — вектор залишків.

Щоб застосувати 1МНК для оцінки параметрів моделі, необхідне виконання таких умов(умови Гаусса-Маркова):

1) математичне сподівання залишків дорівнює нулю, тобто

(2)

2) значення u_i вектора залишків u незалежні між собою і мають постійну дисперсію, тобто

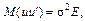(3)

де Е — одинична матриця;

3) незалежні змінні моделі не пов’язані із залишками:

(4)

4) незалежні змінні моделі утворюють лінійно незалежну систему векторів, або, іншими словами, незалежні змінні не повинні бути мультиколінеарними, тобто :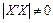

(5)

,

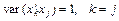де X_k — k-й вектор матриці пояснювальних змінних; X_j — j-й вектор цієї матриці пояснювальних змінних X, .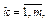

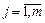Перша умова, здавалося б, є очевидною. Адже коли математичне сподівання залишків не дорівнює нулю, то це означає, що існує систематичний вплив на залежну змінну, а до модельної специфікації не введено всіх основних незалежних змінних. Якщо ця передумова не виконується, то йдеться про помилку специфікації.

зауважимо, що коли економетрична модель має вільний член, то майже завжди за рахунок його значення можна скоригувати рівняння так, щоб математичне сподівання залишків дорівнювало нулю. Отже, для таких моделей перша умова практично виконуватиметься завжди.

Друга умова передбачає наявність сталої дисперсії залишків. Цю властивість називають гомоскедастичністю. Проте вона може виконуватись лише тоді, коли залишки u є помилками вимірювання. Якщо залишки акумулюють загальний вплив змінних, які не враховані в моделі, то звичайно дисперсія залишків не може бути сталою величиною, вона змінюється для окремих груп спостережень. У такому разі йдеться про явище гетероскедастичності, яке впливає на методи оцінювання параметрів.

Третя умова передбачає незалежність між залишками і пояснювальними змінними, яка порушується насамперед тоді, коли економетрична модель будується на базі одночасових структурних рівнянь або має лагові змінні. Тоді для оцінювання параметрів моделі використовуються, як правило, дво- або трикроковий метод найменших квадратів.

Четверта умова означає, що всі пояснювальні змінні, які входять до економетричної моделі, мають бути незалежними між собою. Проте очевидно, що в економіці дуже важко вирізнити такий масив незалежних (пояснювальних) змінних, які були б зовсім не пов’язані між собою. Тоді щоразу необхідно з’ясовувати, чи не впливатиме залежність пояснювальних змінних на оцінку параметрів моделі.

Це явище називають мультиколінеарністю змінних, що призводить до ненадійності оцінки параметрів моделі, робить їх чутливими до вибраної специфікації моделі та до конкретного набору даних. Знижується рівень довіри до результатів верифікації моделей з допомогою 1МНК.Отже, це явище з усіх точок зору є дуже небажаним. Але воно досить поширене. Далі розглянемо методи виявлення мультиколінеарності і способи її врахування з допомогою специфікації моделі чи спеціальних методів оцінювання параметрів.

Скористаємося моделлю (1), для якої виконуються умови (2)–(5), щоб оцінити параметри методом 1МНК.

Рівняння (1) подамо у вигляді: 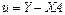. Тоді суму квадратів залишків u можна записати так:

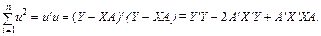
Продиференціюємо цю умову за А і прирівняємо похідні до нуля:

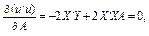
або

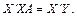(6)

Тут 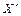— матриця, транспонована до матриці незалежних змінних X.

Звідси

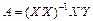(7)

Рівняння (6) дає матричну форму запису системи нормальних рівнянь, а формула (7) показує, що значення вектора А є розв’язком системи таких рівнянь.

Розглянемо приклад оцінювання параметрів моделі 1МНК.