Лекція 3. Статистичні оцінки параметрів розподілу

За так званою “основною теоремою математичної статистики” вважається, що вибіркові характеристики є статистичними оцінками теоретичних характеристик (параметрів) розподілу.

Наприклад, середнє значення з вибірки обсягом n (середнє арифметичне)

будемо вважати оцінкою математичного сподівання M[X] випадкової величини X, якщо варіанти вибірки x1, x2, … xnрозглядати як окремі реалізації (спостереження) цієї випадкової величини. Середнє арифметичне є лінійною функцією результатів спостережень.

Будь-яка функція результатів спостережень, яка не залежить від невідомих параметрів, називається статистикою.

Отже, статистика, яка отримана за результатами спостережень і за якою можна судити про невідоме істинне значення параметра Q, називається оцінкою параметра Q.

Таким чином, в загальному випадку задачу знаходження оцінок параметрів теоретичних розподілів можна сформулювати так: розглядається випадкова величина X, яка підпорядковується деякому теоретичному закону розподілу
F (X, Q ), аналітичний вигляд якого є відомим, аQ – параметр закону розподілу, числове значення якого є невідомим. Провести дослідження для всієї генеральної сукупності неможливо і тоді про параметр Q намагаються судити за вибірками з цієї сукупності.

Отже, із генеральної сукупності розглянемо m вибірок, кожна із яких складається з n незалежних спостережень за об’єктом (i = 1, 2, … n)

Далі вважають, що кожна вибірка – це окремі значення випадкових величин xj(j = 1, 2 … m), які мають закон розподілу F (X, Q). Тоді деяка однозначно визначена функція результатів спостережень над випадковою величиною X

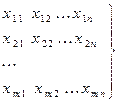
(3.6)

буде оцінкою параметра Q, яку називають точковою.

Зрозуміло, що не кожна статистика може бути оцінкою певного теоретичного параметра. Оскільки результати досліджень випадкові, то будь-яка статистика є випадковою величиною. Для того, щоб статистика могла служити оцінкою деякого параметра Q, необхідно, щоб розподіл цієї статистики був зосередженим достатньо близько від невідомого параметра Q, тобто так, щоб ймовірність великих відхилень статистики від Q була малою. Тоді при систематичному користуванні цієї статистикою як параметром в середньому буде досягатися необхідна точність. Бажано також, щоб при збільшенні кількості спостережень точність результатів оцінювання також збільшувалась.

Для цього оцінки параметрів мають відповідати умовам незміщеності, слушності (обгрунтованості) та ефективності.

Оцінка параметра Q називається незміщеною, якщо її математичне сподівання дорівнює параметру, який оцінюється, тобто

(3.7)

Якщо рівність (3.7) не виконується, тоді оцінка може або збільшувати значення параметра Q, , або зменшувати його . В обох випадках це приводить до систематичних похибок при користуванні оцінкою замість параметрів. Таким чином, вимога незміщеності гарантує відсутність систематичних похибок при користуванні оцінкою Q.

Слушною (обгрунтованою) називають таку статистичну оцінку, яка для n®¥ прямує за ймовірністю до оцінюваного параметра, тобто підпорядковується закону великих чисел

(3.8)

Отже, слушність оцінки свідчить про те, що чим більшим є обсяг вибірки, тим більша ймовірність того, що похибка оцінки не перевищує як завгодно мале додатне число e. Ця властивість більше придатна для вибірок великого обсягу.

Ефективною оцінкою називають таку, яка для заданого обсягу вибірки n має найменшу дисперсію серед всіх можливих незміщених і обгрунтованих оцінок параметра. Якщо і – дві незміщені оцінки параметра Q із дисперсіями і , причому < , тоді оцінка буде ефективнішою оцінкою параметра Q, тому що їй відповідає менше розсіювання окремих значень результатів спостережень навколо центра розподілу. Точкові оцінки, які задовольняють умовам незміщеності, обгрунтованості та ефективності, називаються “найкращими”.

Для отримання “найкращих” оцінок є різні методи, серед яких найбільш поши-рені метод найбільшої правдоподібності (МП-метод), запропонований Ґауссом та узагальнений фішером, і метод моментів, розроблений Пірсоном.

Розглянемо вибірку x1, x2, …, xn, обсяг якої дорівнює n, значень деякої випадкової величини X із функцією густини ймовірностей f (x, Q), яка залежить від параметра Q. Тоді функція, яка має вигляд

, (3.9)

називається функцією правдоподібності.

Нехай X – дискретна випадкова величина, яка набуває значень із частотами m1, m2, …, mrвідповідно і .

У цьому випадку функція правдоподібності матиме вигляд

. (3.10)

Вважатимемо значення відомими та розглянемо як функцію невідомого параметра Q. Значення параметра Q, для яких функція правдоподібності набуває максимуму, називають оцінками максимальної правдопо-дібності.

Виявляється, що для досить загальних умов, що накладаються на функцію розподілу, ці оцінки є асимптотично незміщеними, слушними і ефективними.

Згідно відомих правил диференціального числення для знаходження оцінки максимальної правдоподібності необхідно розв’язати рівняння

(3.11)

і вибрати такий розв’язок , при якому функція набуває максимуму.

Замість рівняння (3.11) зручніше розглядати рівняння вигляду

(3.12)

беручи до уваги не саму функцію (3.9), а її натуральний логарифм.

Якщо є два параметри Q1і Q2, то оцінки їх визначаються зі сумісного розв’язування двох рівнянь

і .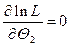

Знайдемо оцінки параметрів нормального розподілу, користуючись МП-методом.

Нехай за даними вибірки x1, x2, …, xn обсягу n спостережень нормально розподіленої випадкової величини X необхідно оцінити два параметри цього закону m та s.

У даному випадку функція правдоподібності L визначається співвідношеннями

,

. (3.13)

Для знаходження оцінок m і s2, продиференціюємо вираз (3.13) по m і s2та прирівняємо до нуля отримані вирази. У результаті отримаємо

,

,

звідки із першого рівняння матимемо

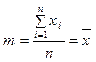, (3.14)

а з другого рівняння отримаємо

. (3.15)

Отже, оцінкою математичного сподівання m є середнє арифметичне , а оцінкою дисперсії s2величина S2, яка називається вибірковою диспер-сією. Метод найбільшої правдоподібності на практиці часто приводить до необхідності розв’язувати доволі складні системи рівнянь. Він не завжди дає оцінки, які є “найкращими”.

Розглянемо метод моментів, запропонований К. Пірсоном. Моменти вибірки вважаються оцінками для моментів розподілу величини X , які залежать від невідомих параметрів. У свою чергу параметри, які оцінюються, можна знайти у вигляді певних функцій від теоретичних моментів, замінивши які їх оцінками, тобто моментами вибіркового розподілу, ми і отримаємо оцінки для невідомих параметрів.

Слід відзначити, що метод моментів іноді приводить до малоефективних оцінок.

Отже, якщо вважати середнє арифметичне початковим вибірковим моментом першого порядку

,

а вибіркову дисперсію S2центральним вибірковим моментом другого порядку

,

то, записуючи вирази для таких моментів будь-якого порядку

, (3.16)

, (3.17)

можна отримати оцінки інших параметрів розподілу випадкової величини X.

У вибірках великого обсягу, коли варіація ознаки вважається неперервною, для знаходження оцінок параметрів користуються інтервальним статистичним рядом. Тоді статистичні оцінки обчислюють за такими наближеними формулами:

, (3.18)

, (3.19)

(3.20)

(3.21)

У виразах (3.18)–(3.21) – середина i-го інтервалу; k - кількість інтервалів; (*) – ознака статистичної оцінки.

“Найкращою” в сенсі незміщеності, слушності та ефективності є середнє арифметичне як оцінка математичного сподівання.

Дійсно, якщо x1, x2, …, xn– незалежні спостереження величини X, тоді

.

Отже, середнє арифметичне є незміщеною оцінкою математичного сподівання. За законом великих чисел відомо, що також є слушною оцінкою

.

Дисперсія середнього арифметичного є найменшою серед дисперсій всіх інших можливих оцінок математичного сподівання. Тому можна вважати ефективною оцінкою математичного сподівання mx, особливо, якщо x підпорядковується нормальному закону розподілу.

Вибіркова дисперсія 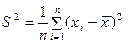не буде незміщеною оцінкою дисперсії генеральної сукупності (тобто теоретичного параметра s2).

Розглянемо X1, X2, …, Xn– взаємно незалежні випадкові величини з математичними сподіваннями

,

та дисперсіями

.

Знайдемо математичне сподівання .

Зобразимо вибіркову дисперсію у вигляді

.

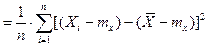Після нескладних алгебраїчних перетворень знайдемо математичне сподівання отриманого виразу

.

Отже, оцінка S2є зміщеною оцінкою параметра . Для того, щоб отримати незміщену оцінку дисперсії, треба зміщену помножити на величину (ця величина називається поправкою Бесселя). Тоді величина

(3.22)

є виправленою дисперсією і незміщеною оцінкою дисперсії генеральної сукупності. Такою оцінкою користуються більше для вибірок малих обсягів.

Отже, для вибірок великих обсягів статистичні оцінки теоретичних параметрів є асимптотично незміщеними, слушними і ефективними. Якщо обсяги вибірок є малими (n < 30), то порушуються властивості “найкращої” оцінки. Відзначимо також, що раніше розглядалося поняття відносної частоти події. Зрозуміло, що відносна частота події є статистичною оцінкою ймовірності події.

Дійсно, з огляду на обмеженість класичної формули для обчислень ймовірностей випадкових подій, ми фактично обчислюємо статистичні оцінки цих ймовірностей у багатьох практичних випадках.