КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функція називається неперервною в точці , якщо для будь-якої послідовності відповідна послідовність значень збігається до .
Функція 
називається неперервною в точці 
, якщо для довільного числа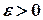 
існує число 
таке, що для всіх 
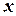, які задовольняють умову 
, виконується нерівність 
.
Наведені означення рівносильні.
Функція називається неперервною в точці справа (зліва), якщо 
.
Отже, функція неперервна в точці , якщо вона неперервна в цій точці як справа, так і зліва.
Покажемо, що неперервна функція характеризується тим, що нескінченно малому приростові аргументу 
відповідає нескінченно малий приріст функції 
.
Дійсно, умову 
можна записати як 
. Тоді
.
Отже, можна дати наступне означення неперервності функції в точці . Функція називається неперервною в точці , якщо нескінченно малому приростові аргументу в цій точці відповідає нескінченно малий приріст функції.
Уведене поняття неперервності функції є локальною (місцевою) властивістю. Якщо функція неперервна в кожній точці інтервалу 
, то говорять, що вона неперервна на інтервалі . Якщо при цьому в точці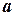 
функція неперервна справа, а в точці 
– неперервна зліва, то говорять, що функція неперервна на відрізку 
.
Зауважимо, що термін неперервної кривої походить із поняття неперервної функції. Графіком неперервної на функції є неперервна крива ("суцільна крива").
Дата добавления: 2014-12-03; просмотров: 23; Нарушение авторских прав
