
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: Коливний рух. Математичний та пружинний маятники. Рівняння гармонічних коливань
Коливальний рух. Вільні й вимушені механічні коливання. Гармонічні коливання. Зміщення, амплітуда, період, частота і фаза гармонічних коливань
Коливаннями або коливальними рухами називають такі види механічного руху чи зміни стану системи, які періодично повторюються в часі, наприклад, механічні коливання тіла на пружині, коливання маятників, коливання струн, вібрації фундаментів будівель, електромагнітні коливання в коливальному контурі.
За фізичною природою коливання поділяють на механічні та електромагнітні, за характером коливань - на вільні, вимушені та автоколивання. Хоча коливання досить різноманітні за своєю фізичною природою, але вони мають спільні закономірності й описуються однотипними математичними методами.
Механічні коливання - періодичне зміщення тіла то в один, то в другий бік відносно положення рівноваги.
Механічна система, в якій одне або декілька тіл можуть здійснювати коливальні рухи, називають коливальною системою.
Коливання, які відбуваються лише під дією внутрішніх сил, називають вільними. Щоб система виконувала ці коливання, треба вивести тіло з положення рівноваги, тобто надати коливальній системі енергію. При цьому рівнодійна всіх сил, що діють на тіло, має бути відмінною від нуля і спрямованою до положення рівноваги, в якому рівнодійна дорівнює нулю. Вільні коливання виникали б, якби не було впливу зовнішніх сил. Цього досягти неможливо, тому вільні коливання це абстракція. Вони з часом стають затухаючими.
Виникла потреба в коливаннях під дією зовнішньої сили, що періодично змінюється, такі коливання називають вимушеними. Ці коливання здійснюють поршні в циліндрах двигунів, голка швацької машини тощо.
Ще одним видом незатухаючих коливань є автоколивання. Це коливання, які підтримуються внутрішніми джерелами енергії системи, коли не діє зовнішня періодична сила. Наприклад, настінний годинник з маятником або наручний механічний годинник - це механічні автоколивальні системи.
У годинниках потенціальна енергія тягарця (або стиснутої пружини) поступово, окремими порціями передається маятнику і компенсує втрати на тертя. Можна спостерігати автоколивання струни під дією смичка, голосових зв'язок під час розмови або співу.
Коливання називають періодичними, якщо значення фізичних величин, які змінюються в процесі коливань, повторюються через однакові проміжки часу. Найпростішим прикладом періодичних коливань є гармонічні коливання, під час яких фізична величина змінюється з плином часу за законом
x = Asin(wt + j0), або x = Acos(wt + j0), (5.1.1)
де А, w, і j0 - постійні величини, причому А > 0, w > 0.
Найпростіший приклад гармонічного коливання - це коливання вздовж осі Ох проекції кінця радіуса-вектора точки, що рухається по колу радіуса А (рис.5.1.2). Якщо t = 0 радіус вектор ОВ утворює з віссю Оу кут j0, а за час t описує кут wt, так що в довільний момент часу x = Asin(wt + j0).
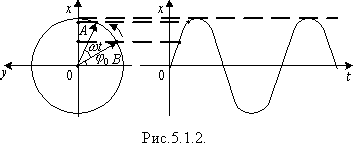
У механічних коливаннях х - зміщення тіла (коливальної системи) від положення рівноваги. У СІ [x] = м; А - амплітуда - найбільше відхилення від положення рівноваги. Якщо коливання незагасальні, то амплітуда не змінюється. У СІ [А] = м.
Мінімальний проміжок часу Т, через який повторюється певне значення змінної величини, що характеризує коливальну систему, називають періодом коливань. Або ж простіше: період - це час одного повного коливання. Якщо за час t відбулося N коливань, тоді
 .
.
У СІ [Т] = c.
Величину, обернену до періоду коливань Т, називають частотою коливань n :
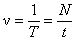 .
.
Частота n показує скільки повних коливань здійснює коливальна система за одиницю часу. У СІ частоту вимірюють у герцах: частота дорівнює 1 Гц, якщо за 1 с коливальна система (маятник) виконує одне повне коливання: [n] = 1 Гц = 1/с = с-1.
У теорії коливань часто користуються циклічною частотою (w) - величиною, яка показує скільки коливань здійснює маятник за 2p секунд. У СІ її вимірюють у герцах (Гц). Між частотою і циклічною частотою існує зв'язок:
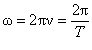 .
.
У рівняннях (5.1.1) вираз в дужках під знаком синуса або косинуса називають фазою коливань j = wt + j0. Фаза коливань визначає при заданій амплітуді стан коливальної системи в довільний момент часу. У СІ цю величину вимірюють у радіанах (рад).
Якщо відлік часу в коливальній системі розпочати з моменту проходження тілом положення рівноваги, то коливання відбуваються за законом синуса, а якщо з точки максимального відхилення - то за законом косинуса.
У формулах (5.1.1) j0 - початкова фаза - показує, на якому етапі знаходився коливальний рух у момент початку відліку часу.
Оскільки механічні коливання відбуваються під дією сил, то при цьому відбувається періодична зміна величини і напряму швидкості та прискорення тіла, що здійснює коливальний рух. Швидкість дорівнює першій похідній від зміщення х:
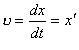 ,
,
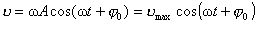 , або
, або 
де 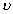 max = wt.
max = wt.
Прискорення дорівнює першій похідній від швидкості або другій похідній від зміщення
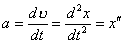
або
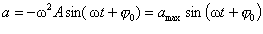 , (5.1.2)
, (5.1.2)
де amax = – w2A.
Порівнюючи вирази (5.1.1) та (5.1.2) дістанемо диференціальне рівняння вільних гармонічних коливань
x" = – w2x
З рівняння (5.1.2) випливає, що під час гармонічних коливань прискорення прямо пропорційне зміщенню ax = – w2x. А згідно з другим законом Ньютона Fx = max = – mw2x. Отже, гармонічні коливання відбуваються під дією сили, напрямленої до положення рівноваги і прямо пропорційної зміщенню від цього положення. Цю силу називають вертальною.
Математичний і пружинний маятники.
Період коливань математичного і пружинного маятників.
Математичний і пружинний маятники є коливальними системами, які за певних умов здійснюють гармонічні механічні коливання.
Математичним маятником називають матеріальну точку, підвішену на невагомій і нерозтяжній нитці. Це ідеальна коливальна система. Якщо подібний маятник не можна вважати матеріальною точкою або не можна знехтувати вагою тіла і розтягом підвісу, то маятник називають фізичним. Такий маятник коливається подібно до математичного.
Підвісимо матеріальну точку масою m на нитці довжиною l і відхилимо отриманий маятник на кут a від положення рівноваги (рис.5.1.3).
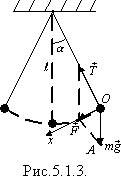
На тіло діятимуть (якщо знехтувати силами тертя і опору повітря) сила тяжіння 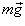 і сила натягу нитки
і сила натягу нитки 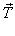 , рівнодійна яких
, рівнодійна яких 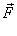 і буде надавати матеріальній точці прискорення. Це прискорення буде напрямлене в бік положення рівноваги. Модуль рівнодійної цих сил (вертикальної сили) знаходимо із прямокутного трикутника FOA:
і буде надавати матеріальній точці прискорення. Це прискорення буде напрямлене в бік положення рівноваги. Модуль рівнодійної цих сил (вертикальної сили) знаходимо із прямокутного трикутника FOA:
F = mgsina.
У разі малих кутів відхилення sina 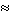 a = x/l. Ураховуючи, що напрям зміщення і вертальної сили протилежні, отримаємо
a = x/l. Ураховуючи, що напрям зміщення і вертальної сили протилежні, отримаємо  , де х - абсолютне значення зміщення маятника від положення рівноваги. Оскільки за другим законом Ньютона F = ma, то прискорення маятника
, де х - абсолютне значення зміщення маятника від положення рівноваги. Оскільки за другим законом Ньютона F = ma, то прискорення маятника 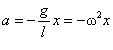 , де
, де  . Період коливань математичного маятника
. Період коливань математичного маятника
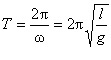 . (5.1.3)
. (5.1.3)
Згідно з формулою (5.1.3) можна зробити висновок, що період коливань математичного маятника не залежить від маси тіла, а визначається лише довжиною підвісу і прискоренням вільного падіння.
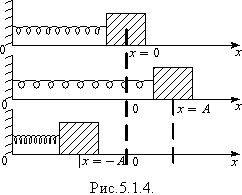
Ще одним прикладом гармонічного коливання є коливання тіла на пружині (рис.5.1.4). У стані рівноваги (рис.5.1.4, положення х = 0) пружина поки що не деформована, тому на тіло сила пружності не діє. Сила тертя між тілом і опорою дорівнює нулю. Сила тяжіння зрівноважена силою реакції опори. Якщо вивести тіло зі стану рівноваги, перемістивши його вздовж осі Ох на відстань x = ± A (ліворуч або праворуч), а потім відпустити, то маятник буде вільно коливатися під дією сили пружності за законом x = Asinwt. Згідно із законом Гука (Fпр)x = – kx. За другим законом Ньютона (Fпр)x = ma, де m - маса тіла пружинного маятника; а - його прискорення, або 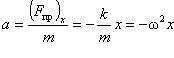 , де
, де 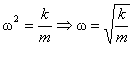 .
.
Період коливань пружинного маятника
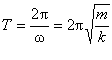 . (5.1.4)
. (5.1.4)
Як видно з формули (5.1.4) період і частота коливань пружинного маятника не залежать від прискорення вільного падіння, а визначаються лише масою підвішеного тіла і жорсткістю пружини.
Перетворення енергії при гармонічних коливаннях.
Явище резонансу під час вимушених механічних коливань.
Розглянемо перетворення енергії під час гармонічних коливань на прикладі пружинного маятника. Уважатимемо систему, що виконує вільні гармонічні коливання під дією пружної сили замкненою. У процесі коливання згідно із законом збереження енергії відбувається перетворення кінетичної енергії в потенціальну і, навпаки, але повна механічна енергія замкненої системи має залишатися незмінною.
З цією метою з'ясуємо, як змінюється в часі кінетична і потенціальна енергії. У формулу кінетичної енергії  підставимо значення швидкості гармонічного коливання:
підставимо значення швидкості гармонічного коливання:
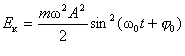 . (5.1.5)
. (5.1.5)
Якщо в певну мить зміщення системи від положення рівноваги дорівнює х, то її потенціальна енергія дорівнює роботі пружної сили. Оскільки під час зміни зміщення від 0 до х величина пружної сили змінюється від F1 = 0 до F2 = kx, то роботу цієї сили розраховують за формулою 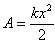 . Отже,
. Отже, 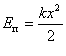 . Підставляючи в цю формулу значення зміщення для гармонічного коливання, одержимо вираз
. Підставляючи в цю формулу значення зміщення для гармонічного коливання, одержимо вираз
 . (5.1.6)
. (5.1.6)
Повна енергія коливальної системи дорівнює сумі кінетичної і потенціальної енергій у заданий момент часу. Додаючи рівняння (5.1.5) і (5.1.6) та враховуючи, що mw2 = k, отримаємо вираз для повної енергії коливальної системи:
 .
.
Таким чином, повна енергія системи, що виконує гармонічні коливання, пропорційна квадрату амплітуди коливань і не залежить від часу. Зі збільшенням кінетичної енергії системи зменшується її потенціальна енергія і, навпаки, але сума кінетичної і потенціальної енергій в довільний момент часу залишається сталою.
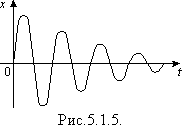
У реальних коливальних системах за рахунок зміни енергії коливального руху виконується робота проти сил тертя й опору. Тому з часом амплітуда вільних коливань зменшується (рис.5.1.5). Коли ж запас енергії вичерпується, коливання припиняються. Коливання, амплітуда яких з часом зменшується, називають затухаючими. Інколи цей процес посилюють за допомогою спеціальних пристроїв. Наприклад, у транспортних засобах використовують різні амортизатори, які гасять коливання кузова, зумовлені нерівностями дороги.
Для того, щоб коливання в системі не загасали, необхідно компенсувати втрати енергії, спричинені дією сили тертя і опору. Енергію в системі треба поповнювати періодично. Це досягається періодичною дією на систему зовнішньої сили. Наприклад, коливання тягарця, підвішеного на пружині, можна підтримувати як завгодно довго, якщо підштовхувати тягарець через рівні проміжки часу.
Коливання системи, які виникають під дією зовнішньої періодично змінної сили, називаються вимушеними.
Зі зміною частоти n зовнішньої сили змінюються амплітуди вимушених коливань. Якщо ця частота наближається до частоти вільних коливань системи n0, то амплітуда вимушених коливань збільшується, досягаючи максимуму, якщо n = n0. Зі збільшенням частоти (n > n0) амплітуда вимушених коливань зменшується. Явище різкого зростання амплітуди вимушених коливань у разі наближення частоти дії зовнішньої періодичної сили до частоти вільних коливань системи називають резонансом. Графік залежності амплітуди коливань від частоти під час резонансу зображено на рис.5.1.6. Резонансна крива тим гостріша, чим менші втрати енергії в системі.

Явище резонансу може бути корисним, оскільки воно дає змогу навіть за допомогою малої сили суттєво збільшити амплітуду, наприклад, укладання бетону за допомогою вібраторів.
Резонанс може бути шкідливим і небезпечним. З метою запобігання цьому слід заздалегідь обчислювати частоти коливань різних машин, засобів транспорту, фундаментів тощо, щоб у звичайних умовах їх експлуатації не міг настати резонанс.
У повсякденному житті можна спостерігати, як в кімнаті бряжчать шибки під час проходження по вулиці важкого вантажного автомобіля. Це означає, що власні частоти коливань шибок дорівнюють частоті коливань деталей автомобіля.
Запитання для самоперевірки
1. Який рух називають коливальним? Що являє собою коливання тіла?
2. Які коливання називають вільними? Наведіть приклади вільних коливань.
3. Які коливання називають вимушеними? Наведіть приклади вимушених коливань.
4. Побудуйте схему і поясніть дослід, що встановлює зв'язок між обертальним і коливальним рухами.
5. Які коливання називають гармонічними? Яке рівняння виражає зміст гармонічного коливання?
6. Що називають амплітудою коливання?
7. Що називають періодом коливань? Яка формула виражає зміст цього поняття? Яка одиниця вимірювання періоду коливань?
8. Що називають частотою коливань? Запишіть формули лінійної і циклічної частот коливань. Назвіть одиниці їх вимірювання.
9. Запишіть формулу, яка встановлює зв'язок між циклічною та лінійною частотами.
10. Наведіть визначення фази гармонічного коливання? Що розуміють під початковою фазою?
11. Що називають зміщенням коливного тіла?
12. Що таке маятник? Який маятник називають математичним?
13. Запишіть рівняння вільних коливань математичного маятника.
14. Запишіть формулу власної циклічної частоти математичного маятника.
15. Який маятник називають пружинним маятником?
16. За якою формулою визначають власну циклічну частоту пружинного маятника?
17. Виведіть формулу періоду вільних коливань пружинного маятника.
18. Опишіть процес перетворення енергії під час гармонічних коливань на прикладі пружинного маятника.
19. За якими формулами визначають повну механічну енергію тіла, що гармонічно коливається, в момент проходження точки рівноваги і крайніх точок руху?
20. За якою формулою визначають повну механічну енергію тіла, що гармонічно коливається, в момент проходження між точкою положення рівноваги і крайньою точкою руху?
21. Чому вільні коливання маятника загасають? За яких умов коливання можуть стати незагасальними?
22. Зобразіть графік загасального коливання.
23. Що називають механічним резонансом? Які умови виникнення резонансу?
24. Наведіть приклади шкідливого і корисного проявів механічного резонансу.
Дата добавления: 2014-12-03; просмотров: 3859; Мы поможем в написании вашей работы!; Нарушение авторских прав |