
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Приклади. 1. Нехай у прямокутній декартовій системі координат рівняння ax+by+cz+d=0 визначає деяку площину
 1. Нехай у прямокутній декартовій системі координат
1. Нехай у прямокутній декартовій системі координат  рівняння ax+by+cz+d=0 визначає деяку площину
рівняння ax+by+cz+d=0 визначає деяку площину  , а також задана точка
, а також задана точка  . Обчислимо відстань
. Обчислимо відстань  від даної точки
від даної точки  до площини
до площини  . Вважатимемо, що точка
. Вважатимемо, що точка  – основа перпендикуляра, опущеного із точки
– основа перпендикуляра, опущеного із точки  на площину
на площину  (рис. 1).
(рис. 1).
|
 перпендикулярний до площини
перпендикулярний до площини  , тому вектори
, тому вектори  та
та  колінеарні, тобто виконується рівність
колінеарні, тобто виконується рівність 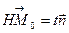 . Прирівнюючи координати векторів, дістаємо
. Прирівнюючи координати векторів, дістаємо
 ,
,  ,
,  ,
,
або  ,
,  ,
,  .
.
Оскільки координати точки  задовольняють рівняння площини
задовольняють рівняння площини  , то виконується рівність
, то виконується рівність  , звідки
, звідки  . Тоді
. Тоді
 =
= 

 .
.
Таким чином,

 . (1)
. (1)
Одержане співвідношення виражає відстань від точки до площини.
 2. Задамо в просторі афінну систему координат та розглянемо площину
2. Задамо в просторі афінну систему координат та розглянемо площину  , задану рівнянням
, задану рівнянням  . Вона розбиває весь простір на два півпростори із спільною границею – площиною
. Вона розбиває весь простір на два півпростори із спільною границею – площиною  . Знайдемо умови, які визначають ці півпростори.
. Знайдемо умови, які визначають ці півпростори.
Виберемо на даній площині деяку точку  та проведемо через неї паралельно до вектора
та проведемо через неї паралельно до вектора  пряму
пряму  (рис. 2). Даний вектор не може бути паралельним до площини
(рис. 2). Даний вектор не може бути паралельним до площини  , оскільки тоді, згідно з лемою про паралельність вектора та площини (лекція 7, п. 3), виконувалася б рівність
, оскільки тоді, згідно з лемою про паралельність вектора та площини (лекція 7, п. 3), виконувалася б рівність  , що неможливо. Нагадаємо, що в прямокутній системі координат вектор
, що неможливо. Нагадаємо, що в прямокутній системі координат вектор  перпендикулярний до площини
перпендикулярний до площини  . Виберемо на прямій
. Виберемо на прямій  довільну точку
довільну точку  та запишемо рівності
та запишемо рівності  , які випливають із колінеарності векторів
, які випливають із колінеарності векторів  та
та  , оскільки останні можна зв’язати між собою рівністю
, оскільки останні можна зв’язати між собою рівністю 
 . Обчислимо значення виразу
. Обчислимо значення виразу  для точки
для точки  :
:






 .
.
Оскільки  , то знак виразу
, то знак виразу  залежить від знаку множника
залежить від знаку множника  . Якщо
. Якщо  , то вектори
, то вектори  та
та  співнапрямлені, тому всі точки
співнапрямлені, тому всі точки  , для яких
, для яких  >0, будуть утворювати півпростір, обмежений площиною
>0, будуть утворювати півпростір, обмежений площиною  (цьому півпростору належить кінець вектора
(цьому півпростору належить кінець вектора  ). При
). При  вектори
вектори  та
та  напрямлені протилежно, тому множина точок, для яких
напрямлені протилежно, тому множина точок, для яких  <0, утворює інший півпростір, границею якого є площина
<0, утворює інший півпростір, границею якого є площина  .
.
3. Дослідимо взаємне розташування двох площин  , заданих в деякій афінній системі координат рівняннями
, заданих в деякій афінній системі координат рівняннями
 ,
,  .
.
Очевидно, що площини  та
та  можуть бути паралельними (зокрема співпадати), або перетинатись. У першому випадку можна говорити про відстань між ними, а у другому – про кут між площинами.
можуть бути паралельними (зокрема співпадати), або перетинатись. У першому випадку можна говорити про відстань між ними, а у другому – про кут між площинами.
Дослідимо умову паралельності площин. Нехай  . Розглянемо паралельні до площини
. Розглянемо паралельні до площини  вектори
вектори  та
та  (нагадаємо, що вектор
(нагадаємо, що вектор  паралельний до площини
паралельний до площини  тоді і тільки тоді, коли виконується рівність
тоді і тільки тоді, коли виконується рівність  ). Для того, щоб площини
). Для того, щоб площини  та
та  були паралельними, необхідно і достатньо, щоб ці вектори були паралельними до площини
були паралельними, необхідно і достатньо, щоб ці вектори були паралельними до площини  , тобто повинні виконуватися рівності
, тобто повинні виконуватися рівності
 ,
,  . (2)
. (2)
Звідси дістаємо умову паралельності площин
 (3)
(3)
у випадку, коли  ,
,  та
та  відмінні від нуля. Зауважимо, що у випадку паралельності площин, якщо
відмінні від нуля. Зауважимо, що у випадку паралельності площин, якщо  , то
, то  . Справді, якби
. Справді, якби  0 і
0 і  , то площина
, то площина  була б паралельна осі
була б паралельна осі  , в той час, коли площина
, в той час, коли площина  до осі
до осі  не паралельна. При
не паралельна. При  з рівності (2) дістаємо
з рівності (2) дістаємо  . Аналогічно, при
. Аналогічно, при  дістаємо
дістаємо  . Тобто якщо деякі із коефіцієнтів біля змінних в рівнянні однієї з площин рівні нулю, то для паралельності площин необхідно, щоб у рівнянні другої площини відповідні коефіцієнти теж дорівнювали нулю.
. Тобто якщо деякі із коефіцієнтів біля змінних в рівнянні однієї з площин рівні нулю, то для паралельності площин необхідно, щоб у рівнянні другої площини відповідні коефіцієнти теж дорівнювали нулю.
Нехай  та
та  ,
,  ,
,  . Вважатимемо також, що точка
. Вважатимемо також, що точка 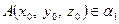 . Площини
. Площини  та
та  співпадатимуть, якщо точка
співпадатимуть, якщо точка  . Із рівностей
. Із рівностей  ,
,  , помноживши другу із них на
, помноживши другу із них на  та віднявши від першої, дістаємо
та віднявши від першої, дістаємо  . Звідси дістаємо умову співпадання двох площин у виді пропорції
. Звідси дістаємо умову співпадання двох площин у виді пропорції

(наявність нуля в одному із знаменників вимагає рівності нулю відповідного чисельника).
 Нехай умова (3) паралельності площин не виконується, тобто площини перетинаються. При перетині двох площин утворюються чотири двогранні кути, величини яких ми хочемо визначити, користуючись рівняннями площин. Вважатимемо систему координат прямокутною декартовою. Оскільки вектор
Нехай умова (3) паралельності площин не виконується, тобто площини перетинаються. При перетині двох площин утворюються чотири двогранні кути, величини яких ми хочемо визначити, користуючись рівняннями площин. Вважатимемо систему координат прямокутною декартовою. Оскільки вектор  та вектор
та вектор  , то кут
, то кут  між векторами
між векторами  та
та  буде рівний одному із двогранних кутів між площинами (рис. 3).
буде рівний одному із двогранних кутів між площинами (рис. 3).
Скориставшись скалярним добутком векторів  та
та  , дістаємо
, дістаємо
 Зокрема площини будуть перпендикулярними тоді і тільки тоді, коли
Зокрема площини будуть перпендикулярними тоді і тільки тоді, коли  , тобто, коли виконується умова
, тобто, коли виконується умова
 .
.
4. Нехай площини  та
та  будуть паралельні. Тоді їхні рівняння можна записати у виді
будуть паралельні. Тоді їхні рівняння можна записати у виді
 ,
,  .
.
Знайдемо відстань  між даними площинами. Якщо точка
між даними площинами. Якщо точка  , то шукана відстань
, то шукана відстань  буде дорівнювати відстані від цієї точки до площини
буде дорівнювати відстані від цієї точки до площини  . Користуючись формулою відстані від точки до площини з пункту 1, дістаємо
. Користуючись формулою відстані від точки до площини з пункту 1, дістаємо
 .
.
5. Взаємне розташування двох площин можна досліджувати і іншими способами, зокрема, користуючись методами лінійної алгебри. Покажемо, як використовується цей метод при дослідженні взаємного розташування трьох площин  , заданих рівняннями
, заданих рівняннями
 ,
, 
 .
.
Дослідимо систему рівнянь
 . (4)
. (4)
Для цього введемо в розгляд матриці
 та
та  і позначимо їхні ранги відповідно через
і позначимо їхні ранги відповідно через  та
та  .
.
Можливі наступні випадки:
a)  . В цьому випадку система (4) має єдиний розв’язок, а площини
. В цьому випадку система (4) має єдиний розв’язок, а площини  мають єдину спільну точку;
мають єдину спільну точку;
б)  . Система (4) має однопараметричну нескінченну сім’ю розв’язків. Всі три площини в цьому випадку перетинаються по спільній прямій або дві з площин співпадають; а третя їх перетинає.
. Система (4) має однопараметричну нескінченну сім’ю розв’язків. Всі три площини в цьому випадку перетинаються по спільній прямій або дві з площин співпадають; а третя їх перетинає.
в)  . Система (4) має двопараметричну нескінченну сім’ю розв’язків, тобто, рівносильна одному із трьох її рівнянь. У цьому випадку всі три площини співпадають;
. Система (4) має двопараметричну нескінченну сім’ю розв’язків, тобто, рівносильна одному із трьох її рівнянь. У цьому випадку всі три площини співпадають;
г)  ,
,  . Система (4) розв’язків не має. Площини попарно перетинаються по трьох паралельних прямих, або дві з площин паралельні, а третя їх перетинає;
. Система (4) розв’язків не має. Площини попарно перетинаються по трьох паралельних прямих, або дві з площин паралельні, а третя їх перетинає;
д)  ,
,  . Система (4) розв’язків не має. У цьому випадку площини паралельні між собою (можливий випадок співпадання двох із них).
. Система (4) розв’язків не має. У цьому випадку площини паралельні між собою (можливий випадок співпадання двох із них).
6. Наведемо приклади.
Задача 1. Визначити, на якій відстані від початку координат проходить площина  , задана рівнянням
, задана рівнянням  .
.
Розв’язання. Користуючись рівністю (1), дістаємо 
Відповідь: 2.
Задача 2. У трикутній піраміді SABC ребра SA, SB та SC взаємно перпендикулярні та рівні відповідно  . Обчислити довжину висоти SH.
. Обчислити довжину висоти SH.
Розв’язання. Введемо прямокутну систему координат, вибравши початок координат в точці 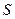 та вибравши за напрямки осей
та вибравши за напрямки осей  відповідно напрямки променів SA, SB та SC. Оскільки на осях
відповідно напрямки променів SA, SB та SC. Оскільки на осях  та
та  площина ABC відтинає відповідно відрізки
площина ABC відтинає відповідно відрізки  та
та  , то її рівняння запишеться у виді
, то її рівняння запишеться у виді  . Скориставшись формулою (1), одержуємо довжину висоти SH, як відстань від точки
. Скориставшись формулою (1), одержуємо довжину висоти SH, як відстань від точки  до площини (ABC):
до площини (ABC):  .
.
Задача 3. Встановити, чи перетинає площину, яка задана рівнянням  , відрізок, кінці якого знаходяться в точках
, відрізок, кінці якого знаходяться в точках  та
та  .
.
Розв’язання. Визначимо знак виразу  для кожної із заданих точок. Знаходимо
для кожної із заданих точок. Знаходимо  ,
,  . Оскільки обидві точки розташовані в одному півпросторі, то відрізок площину не перетинає.
. Оскільки обидві точки розташовані в одному півпросторі, то відрізок площину не перетинає.
Задача 4. Скласти рівняння площини, яка проектує пряму  на площину
на площину  , яка задана рівнянням
, яка задана рівнянням  .
.
Розв’язання. Очевидно, що проектуюча площина паралельна до векторів  та
та  , перший з яких паралельний до заданої прямої, а другий перпендикулярний до площини
, перший з яких паралельний до заданої прямої, а другий перпендикулярний до площини  . Крім цього, площина повинна проходити через точку
. Крім цього, площина повинна проходити через точку  , яка належить прямій. Рівняння шуканої площини запишемо у вигляді визначника
, яка належить прямій. Рівняння шуканої площини запишемо у вигляді визначника  . Після очевидних обчислень дістаємо шукане рівняння
. Після очевидних обчислень дістаємо шукане рівняння  .
.
Відповідь:  .
.
Дата добавления: 2014-12-03; просмотров: 172; Мы поможем в написании вашей работы!; Нарушение авторских прав |