Скорости точек тела при плоскопараллельном движении 2 страница

По теореме синусов

,

откуда

.

Подставив в уравнение значение скорости ветра

20·3,6 = 72 км/ч,

получим

α = 3°45′.

Найдем третий угол треугольника:

β = 180° – 150° – 3°45′ = 26°15′.

Тогда

V_а = 486 км/ч.

Время перелета

t = ; t = 1 ч 39 мин.

Контрольные вопросы

1. Определение скорости точки при задании ее движения векторным, координатным и естественным способами.

2. Определение ускорения точки при задании ее движения векторным, координатным и естественным способами.

3. Какое движение твердого тела называют поступательным? Как оно задается?

4. Какое движение твердого тела называется вращением вокруг неподвижной оси и как оно осуществляется?

5. Что называют угловой скоростью вращения? Как она определяется?

6. Как вводится понятие «угловое ускорение»? Что оно характеризует?

7. Запишите формулы, по которым определяются скорость, касательное, нормальное и полное ускорения любой точки тела, вращающегося вокруг неподвижной оси.

8. Дайте определения понятиям «вектор угловой скорости» и «вектор углового ускорения». Как они направлены и где они приложены?

9. Уравнения равномерного и равнопеременного вращения тела вокруг неподвижной оси.

10. Какое движение твердого тела называют плоскопараллельным? Почему для характеристики этого движения достаточно трех уравнений?

11. Разложение плоскопараллельного движения на поступательное и вращательное.

12. Как определяются скорости точек тела при плоскопараллельном движении?

13. Теорема о проекциях скоростей двух точек плоской фигуры на ось, проходящую через эти точки.

14. Что такое мгновенный центр скоростей? Как определяется его положение? Назовите частные случаи определения.

15. Как определяются скорости точек тела при плоском движении с помощью мгновенного центра скоростей?

16. Докажите теорему об ускорениях точек тела при плоскопараллельном движении.

17. Абсолютное, относительное и переносное движения точки. Приведите примеры. Скорости и ускорения.

18. Теорема о сложении скоростей при сложном движении точки.

19. Теорема о сложении ускорений при сложном движении точки.

20. Что характеризует и как определяется поворотное ускорение?

21. Сформулируйте правила определения направления поворотного ускорения.

Динамика

Тема 12. Основные законы механики. Две задачи динамики

Динамикой называется наиболее общая часть теоретической механики, в которой изучается зависимость между механическим движением материальных тел и действующими на них силами.

Основоположником динамики является И. Ньютон (1642–1727). Он сформулировал основные законы динамики, обобщил понятие силы, ввел понятие массы, открыл закон всемирного тяготения, – все это лежит в основе современной механики и физики.

1-й закон Ньютона (закон инерции): изолированная материальная точка движется pавномеpно и пpямолинейно либо находится в покое, до тех поp, пока действие дpугих тел на эту материальную точку не изменит этого состояния.

Свойства изолированной материальной точки сохранять состояние равномерного и прямолинейного движения называется свойством инертности.

2-й закон Ньютона (основной закон динамики): скорость изменения количества движения материальной точки равна силе, действующей на эту точку (рис. 3.1.85). Математически этот закон Ньютона представим равенством

, (3.1.90)

где m – масса точки;

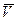– скорость точки;

– количество движения точки

Принимая m = const, получим

или . (3.1.91)

Это уравнение называется основным уравнением динамики материальной точки: действующая на материальную точку сила равна произведению массы точки на ее ускорение.

Следовательно, векторы и 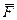наплавлены по одной прямой. Этот закон выражает количественное соотношение между тремя физическими величинами: массой, силой и ускорением.

Массой материальной точки называется физическая величина, являющаяся мерой ее инертности и гравитационных свойств.

Сила является количественной мерой взаимодействия материальных тел друг с другом.

Из 2-го закона Ньютона следует, что если сила , то ; .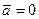

Это означает, что между 1-м и 2-м законами Ньютона имеется полное соответствие. Эти законы относятся к динамике материальной точки и справедливы только в инерциальной системе координат – системе, движущейся поступательно, прямолинейно и равномерно. Это гелиоцентрическая система с началом в центре Солнца и осями, направленными на так называемые неподвижные звезды. При решении большинства технических задач инерциальной можно считать систему отсчета, жестко связанную с Землей.

Закон независимости действия сил:ускорение материальной точки, возникающее при одновременном действии на нее нескольких сил, равно геометрической сумме ускорений, сообщаемых точке отдельными силами.

Этот закон вытекает из аксиомы о параллелограмме сил. Уравнение, выражающее основной закон динамики, принимает следующий вид:

или . (3.1.91')

3-й закон Ньютона (закон равенства действия и противодействия двух материальных тел):силы взаимодействия двух тел (действия и противодействия) равны по величине, направлены в противоположные стороны и имеют общую линию действия (рис. 3.1.86).

3-й закон Ньютона относится к динамике системы и справедлив в любой системе координат, т. к. он не содержит кинематических характеристик движущихся материальных объектов. Действие и противодействие приложены к различным материальным телам, поэтому не уравновешиваются.

Дифференциальные уравнения движения материальной точки.Используя основной закон динамики, можно вывести дифференциальные уравнения движения материальной точки в различных системах координат (рис. 3.1.87 и 3.1.88). Вспоминая, что

,

где 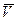– вектор скорости, 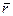– радиус-вектор точки,

можно записать уравнение (3.1.91) следующим образом:

. (3.1.92)

От векторной формы основных соотношений перейдем к аналитической форме в проекциях на оси

m 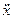= F_х = X;

m = F_y = Y; (3.1.93)

m = F_z = Z.

Большое значение имеют также дифференциальные уравнения в проекциях на естественные оси (направления касательной, нормали и бинормали к траектории):

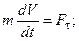
. (3.1.94)

Первая задача динамики материальной точки.Зная массу точки (m) и уравнения ее движения x = f₁(t), y = f₂(t), z = f₃(t), можно найти модуль и направление равнодействующей сил, приложенных к точке. Эта задача легко решается путем дифференцирования уравнений движения, и решение получается непосредственно из уравнений (3.1.93)

X = m 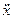; Y = m ; Z = m ;

F = ,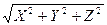

cos( ) = ;

Обратная (вторая) задача динамики материальной точки. Зная силы, действующие на материальную точку, ее массу m, а также начальное положение точки М₀ (x₀, y₀, z₀) и ее начальную скорость V₀ (x₀, y₀, z₀), требуется найти закон движения этой точки.

Под действием одной и той же силы материальная точка может совершать целый класс движений, определяемых начальными условиями движения:

x = f₁(t; x₀, y₀, z₀; );

y = f₂(t; x₀, y₀, z₀; 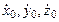); (3.1.95)

z = f₃(t; x₀, y₀, z₀; ).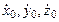

Решение этой задачи сводится к интегpиpованию дифференциальных уравнений (3.1.93), в которых масса, а также проекции силы известны. При интегрировании каждого дифференциального уравнения движения точки появляются две постоянные. Значения этих постоянных определяют по начальным условиям движения.

Во второй основной задаче динамики рассматриваются четыре случая:

1. Сила постоянна по модулю и направлению (имеем случай равнопеременного движения, т.е. движения с постоянным ускорением).

2. Сила зависит от времени (это происходит, когда ее изменяют путем регулирования, как, например, регулируют силу тяги ВС путем изменения режима работы его двигателей).

3. Сила зависит от положения точки в пространстве (силу, зависящую от координаты x, может создать сжатая или растянутая пружина и другие упругие тела при их деформации).

4. Сила зависит от скорости точки (это, прежде всего, сила сопротивления, когда материальная точка движется в какой-либо среде, например, в воздухе, воде и т.д.).

Свободные прямолинейные колебания материальной точки. Материальная точка М массой m движется прямолинейно под действием восстанавливающей силы F, направленной к центру колебания О (рис. 3.1.89):

F = – cx,

где c – постоянный коэффициент пропорциональности.

Дифференциальное уравнение колеблющейся материальной точки выглядит следующим образом:

m 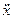= – cx. (3.1.96)

Разделим левую и правую часть на m и введем обозначение c/m = k² и перенесем в левую часть:

= 0. (3.1.97)

Получили линейное дифференциальное уравнение 2-го порядка с постоянными коэффициентами. Общее решение этого уравнения имеет вид

x = C₁coskt + C₂sinkt, (3.1.98)

где C₁ и C₂ – произвольные постоянные, определяемые по начальным условиям движения t = 0, x = x₀ , V = V₀.

Уравнение (3.1.98) – уравнение гармонических колебаний материальной точки:

V = dx/dt = – C₁ ksinkt + C₂ kcoskt; (3.1.99)

x₀ = C₁, V₀ = C₂ k Þ C₁ = x₀, C₂ = V₀/k.

Подставив в уравнение (3.1.98), получим искомый закон движения точки М

. (3.1.100)

Для анализа свободных колебаний дифференциальное уравнение (3.1.98) лучше представить в амплитудной форме, где C₁ = A sinα, C₂ =A cosα:

x = A sin(kt +α), (3.1.101)

следовательно, в случае прямолинейного движения под действием притягивающей силы, пропорциональной расстоянию от центра притяжения, материальная точка совершает гармонические колебания.

Величина наибольшего отклонения точки М от центра О, называется амплитудой – (A) колебания; аргумент (kt + α) называется фазой колебания; α – начальной фазой колебания; k – круговой частотой колебаний. Графиком гармонических колебаний является синусоида.

Скорость точки определяется по формуле

V = dx/dt = Аkcos(kt + α). (3.1.102)

Амплитуда A и начальная фаза α определяются по начальным условиям движения.

Пусть при t = 0, абсцисса точки М = x₀, а скорость V₀, тогда x₀ = Аsinα, V₀ = Аkcosα, получаем

А = и tgα = . (3.1.103)

Найдем полный период колебаний, т.е. тот промежуток времени, по истечении которого точка возвращается в данное положение с той же самой скоростью:

T = 2π/k или T = 2π . (3.1.104)

Частота и период свободных колебаний точки зависят лишь от массы этой точки и от коэффициента с, характеризующего восстанавливающую силу, и не зависят от начальных условий движения, k = 2π/T – круговая частота колебаний, определяющая число полных колебаний, которые совершает точка в течение 2π секунд.

Принцип Даламбера для материальной точки.Принципом Даламбера называют метод, позволяющий решать задачи динамики приемами статики.

Пусть точка М массой m движется по некоторой поверхности с ускорением под действием активных сил, равнодействующая которых равна , на нее наложены связи (рис. 3.1.90). Основное уравнение динамики имеет вид

; (3.1.105)

.

Введем обозначение

, (3.1.106)

тогда уравнение (3.1.105) примет вид

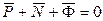. (3.1.107)

Уравнение (3.1.107) выражает принцип Даламбера: если в каждый данный момент к действующим на точку активным силам и реакциям связи условно присоединить силу инерции, то полученная система сил будет находиться в воображаемом равновесии и по отношению к ней будут справедливы уравнения статики.

Сила инерции реально существует в природе, но в действительности она приложена не к движущейся точке, а к тому телу, от взаимодействия с которым эта точка получает данное ускорение.

Силой инерции называется сила , равная по модулю произведению массы точки на ее ускорение и направленная противоположно этому ускорению.

Проецируя уравнение (3.1.106) на оси декартовых координат, получим

. (3.1.108)

Проецируя уравнение (3.1.109) на естественные оси, получим (рис. 3.1.91)

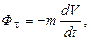
. (3.1.109)

Тема 13. Динамика относительного движения материальной точки

Пусть материальная точка массой m движется по отношению к системе отсчета , которая, в свою очередь, обладает некоторым движением по отношению к инерциальной (неподвижной) системе отсчета охуz (рис.3.1.92). Обозначим через 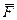равнодействующую приложенных к точке активных сил, через – равнодействующую реакций связей.

На основании 2-го закона Ньютона

,

где – абсолютное ускорение точки.

На основании теоремы Кориолиса

,

тогда

или .

Векторы (–m ) и (–m ) называются соответственно переносной и кориолисовой силами инерции. Введя обозначение и 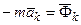, получаем

. (3.1.110)

Выражение (3.1.110) представляет собой основное уравнение динамики относительного движения материальной точки. В случае непоступательного переносного движения относительное движение материальной точки можно рассматривать как абсолютное, если к действующим на точку силам присоединить переносную и кориолисову силы инерции.

Рассмотрим некоторые частные случаи.

1. Подвижная система отсчета движется поступательно: ω_e = 0, = 0, = 0. Уравнение (3.1.110) примет вид

. (3.1.111)

2. Подвижная система отсчета движется поступательно, прямолинейно и равномерно = 0, = 0 и , . Уравнение (3.1.110) примет вид

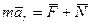, (3.1.112)

т.е. основное уравнение динамики имеет такой же вид, как в случае неподвижной системы отсчета. Иными словами, рассматриваемая система отсчета является инерциальной.

Отсюда вытекает принцип относительности классической механики, установленный Галилеем: «В системе отсчета, движущейся поступательно, прямолинейно и равномерно относительно неподвижной системы, все механические явления происходят так же, как и в неподвижной системе, в силу чего никакими механическими экспериментами такое движение системы отсчета не может быть обнаружено».

3. Точка по отношению к подвижным осям находится в покое: 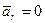и , а, следовательно, и Уравнение (3.1.110) примет вид

. (3.1.113)

Таким обpазом, в случае, когда материальная точка находится в состоянии относительного покоя, геометpическая сумма фактически пpиложенных к точке сил и пеpеносной силы инеpции pавна нулю

Случаи относительного покоя, пеpегpузки, испытываемые пилотом. Интересным примером относительного равновесия является равновесие пилота в системе отсчета, связанной с ВС. Определим перегрузку, действующую на пилота в различных режимах полета.

Перегрузкой, испытываемой пилотом в полете, называют векторную физическую величину, равную отношению вектора силы, с которой кресло и привязные ремни действуют на пилота в полете, к произведению массы пилота на ускорение свободного падения:

.

В полете на пилота фактически действуют только две силы: реакция со стороны кресла и привязных ремней, а также сила тяжести.

Таким образом, условие относительного равновесия для данного случая может быть записано в следующем виде:

,

откуда, учитывая, что и , находим

.

Переносное ускорение можно принять равным ускорению центра масс самолета, которое найдем из основного закона динамики

m_c = ,

где – сила тяги двигателя,

– подъемная сила,

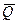– сила лобового сопротивления,

– сила бокового давления.

Тогда

= ;

. (3.1.114)

Разложим перегрузку по осям ВС на три составляющие: продольную ( ), направленную по продольной оси ВС, нормальную (n_y = Y /G_c), направленную по главной нормали к траектории движения ВС, и боковую (n_z= Z /G_c).

Боковая составляющая n_z обычно равна нулю, так как в нормальных условиях ВС летит без бокового скольжения. Продольная составляющая n_х мала, так как разность между силой тяги двигателя и силой лобового сопротивления обычно мала, за исключением непродолжительных режимов ускорения после включения форсажа. Следовательно, основной составляющей перегрузки в полете при выполнении пилотажных фигур является нормальная составляющая перегрузки, равная отношению подъемной силы к силе тяжести.

В полете можно на некоторое время создать такой режим, называемый состоянием динамической невесомости, когда перегрузка, действующая на пилота, равна нулю. Для этого необходимо силу лобового сопротивления уравновесить силой тяги двигателя, а с помощью рулей при выполнении горки выдержать режим нулевой подъемной силы.

Рассмотрим криволинейное движение ВС и перегрузки, действующие при этом.

При движении по дуге радиусом R, расположенной в вертикальной плоскости, ВС имеет ускорение, и, следовательно, силы и не уравновешены. Но, приложив силы инерции, мы сможем использовать уравнения равновесия (рис. 3.1.93).

Приложим и составим уравнение равновесия в проекции на ось OY:

Y – mg – Ф_n = 0 или Y = mg + m ,

разделим на mg, пролучим

или

n_y = 1 + . (3.1.115)

Таким образом, перегрузка возрастает с увеличением скорости и уменьшением радиуса траектории полета.

Перегрузка n_y не равна единице и при разворотах ВС. Правильный разворот выполняют по дуге окружности в горизонтальной плоскости с постоянной скоростью. И в этом случае силы, действующие на ВС, не уравновешены (рис. 3.1.94).

Рис. 3.1.94

Составим условие равновесия сходящихся сил, где угол γ равен углу крена ВС. Решая треугольник сил, получим

cosγ = ,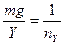

тогда

и . (3.1.116)

Как следует из формулы (3.1.116), перегрузка n_y увеличивается с увеличением крена, который, в свою очередь, зависит от скорости ВС и радиуса разворота. Например, при крене γ = 10° n_y = 1,01, при γ = 30° n_y =1,16, при γ = 60° n_y = 2. Для пассажирских самолетов крен более 30° не допускается. Максимально допустимая перегрузка ограничена, исходя из соображений прочности самолета. Как правило, она не превышает n_max = 2,5–2,8.