
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эквивалентная длина трубы
Иногда местные сопротивления выражают в виде эквивалентной длины прямого участка трубы. Эквивалентная длина – это длина условного трубопровода, гидравлические потери на котором равны местным потерям.

hм.с. =  ; hтр. = l
; hтр. = l  .
.
Приравниваем hм.с. = hтр, тогда  = l
= l  .
.
Отсюда z= l  или lэкв.= zd/l..
или lэкв.= zd/l..
Общие потери напора h = l  ,где lрасч.= l + lэкв.
,где lрасч.= l + lэкв.
Так как коэффициент трения l зависит от числа Рейнольдса, то и эквивалентная длина трубы будет различной в зависимости от значения числа Рейнольдса.
2.6. Истечение жидкости через отверстия и насадки
Истечение жидкости через отверстия и насадки различных форм является весьма распространенным процессом. На практике часто приходится встречаться с истечением через отверстия в тонкой стенке, цилиндрические, конические сходящиеся и расходящиеся, а также коноидальные (воронкообразные) насадки. Такие элементы гидравлических систем используются в установках для разрушения и размыва породы (гидромониторы); для тушения пожаров; с целью распыления и дробления жидкости (дождевальные установки, подача топлива в камеры сгорания); для дозирования жидкости (жиклеры карбюраторов); для измерения времени опорожнения сосудов и т.д.
Этот случай движения жидкости характерен тем, что в процессе истечения часть потенциальной энергии, которой обладает жидкость в резервуаре, за исключением потерь, превращается в кинетическую энергию свободной струи.
Основными задачами является определение скорости истечения и расхода жидкости для различных форм отверстий и насадков.
2.6.1. Истечение жидкости через малое отверстие в тонкой стенке
при постоянном напоре
Классификация отверстий по их размерам:
а) малые dо < 0,1Н;
б) средние 0,1Н £ dо£ 0,4Н;
в) большие dо > 0,4Н,
где dо – диаметр отверстия; Но = const – напор в сосуде.
Кроме того, отверстия по форме могут быть круглые и некруглые.
Стенка считается «тонкой» при условии, что толщина стенки d < 0,2dо и не влияет на форму и условия истечения струи.

Пусть жидкость вытекает из резервуара в воздушное пространство с давлением р1.
При истечении жидкости через малое отверстие в тонкой стенке вследствие влияния сил инерции происходит уменьшение поперечного сечения струи по отношению к сечению отверстия. Цилиндрическую форму струя принимает на расстоянии, равном примерно одному диаметру отверстия. Здесь располагается «сжатое сечение», в котором площадь струи минимальна.
Степень сжатия струи оценивается коэффициентом сжатия, равным отношению площади сжатого поперечного сечения струи к площади отверстия: e = sc/so = (dc/do)2.
Если выполняется условие l > 3 dо, стенки сосуда не влияют на формирование сжатого сечения, то наблюдается совершенное сжатие струи (максимально возможное). При невыполнении этого требования - сжатие несовершенное. Несовершенное сжатие может быть полным и неполным. Если часть периметра отверстия совпадает с направляющими гранями сосуда, то сжатие называется неполным.

1 – совершенное сжатие, 2 – несовершенное полное сжатие, 3 и 4 – неполное сжатие.
Запишем уравнение Бернулли в напорах для сечений 0-0 и 1-1:
z0 + р0/ρg = z1 + р1/ρg + av2/2g + zv2/2g, так как v0 = 0.
Здесь z - коэффициент сопротивления отверстия.
Вводя обозначения: z0 - z1 = Н0; Н0 +  = Н – расчетный напор, получаем
= Н – расчетный напор, получаем
Н =  , откуда скорость истечения
, откуда скорость истечения
v =  , где j =
, где j =  - коэффициент скорости.
- коэффициент скорости.
Для идеальной жидкости z = 0, a = 1, тогда j = 1 и vт =  - теоретическая скорость истечения зависит только от напора.
- теоретическая скорость истечения зависит только от напора.
Коэффициент скорости выражает отношение действительной скорости истечения к теоретической j = vд /vт £ 1. Уменьшение действительной скорости по отношению к теоретической происходит за счет потери части напора при истечении реальной жидкости.
Если истечение происходит в атмосферу, то давление по всему сечению цилиндрической струи равно атмосферному.
Теоретический расход Qт = sovт = so  .
.
Действительный расход Qд = sсvд = esoj  = m so
= m so  = mQт ,
= mQт ,
где m = ej = Qд/Qт < 1 – коэффициент расхода, выражающий отношение действительного расхода к теоретическому. Коэффициент расхода всегда меньше 1, так как при истечении идеальной жидкости через отверстие сжатие струи будет иметь место и при отсутствии гидравлических потерь.

Рис. Зависимость e, j и m от Reи для круглого отверстия в тонкой стенке
Значения коэффициентов истечения зависят прежде всего от типа отверстия или насадка, а также от числа Рейнольдса.
На рисунке показаны зависисмости коэффициентов e,j и m для круглого малого отверстия от Reи, подсчитанного по идеальной скорости истечения:
Reи =  =
=  .
.
При больших значениях чисел Рейнольдса – квадратичная область истечения.
При расчетах для маловязких жидкостей обычно принимают следующие значения коэффициентов истечения:
j = 0,97; m = 0,62; e = 0,64; z = 0,065.
При истечении жидкости под действием сил поверхностного натяжения происходит изменение формы струи по отношению к форме отверстия. Это явление называется инверсией струи.
2.6.2. Истечение через насадки при постоянном напоре
Насадками называются короткие трубки, длиной 3¸4 диаметра, различной формы, присоединенные к отверстию. Насадки бывают длинные и короткие; внешние и внутренние; по виду отверстия - цилиндрические, конические сходящиеся и расходящиеся, коноидальные насадки.
Коноидальный насадок, или сопло, близок по форме естественно сжимающейся струе. Он очень распространен, так как имеет очень малые потери и поэтому коэффи-циент расхода близок к единице.
Рассмотрим истечение через внешний цилиндрический насадок.
Возможны два режима истечения жидкости через цилиндрический насадок: со сжатием и без сжатия струи.
1-й режим. При входе в насадок струя слегка сжимается, а затем постепенно расширяется до размеров отверстия и выходит полным сечением.
В – область завихренности потока.

Так как коэффициент сжатия струи e = 1, тогда коэффициент скорости равен коэффициенту расхода j = m..
2-й режим. При некотором соотношении l/d и Re наступает 2-й режим истечения, когда струя сжимается и выходит из насадка сжатым сечением.

Напор, при котором происходит переход от одного режима к другому, называется критическим. При напоре, равном критическому, происходит внезапное изменение режима истечения. При Н > Нкр. 1-й режим истечения невозможен.
Таблица коэффициентов истечения отверстий и насадков
в квадратичной области истечения
| Тип отверстия или насадка | m | j | e | z | Применение |
| 1. Малое отверстие | 0,62 | 0,97 | 0,64 | 0,06 | В гидравлических системах |
| 2. Внешний цилиндрический насадок | 0,82 | 0,82 | 1,0 | 0,5 | Для увеличения расхода. Дренаж под дорогами. Водовыпуск из плотин |
| 3. Внутренний цилиндрический насадок | 0,71 | 0,71 | 1,0 | 1,0 | - ¤¤ - |
| 4. Конический сходящийся насадок Ө = 15° | 0,94 | 0,96 | 0,98 | 0,06¸0,09 | Сопла турбин, гидромониторы, брандсбойты |
| 5. Конический расходящийся насадок Ө = 6°¸1° | 0,55 | 0,55 | 1,0 | 3¸4 | Отсасывающие каналы гидротурбин |
| 6. Коноидальный насадок | 0,98 | 0,98 | 1,0 | 0,03¸0,1 | Сопла турбин, гидромониторы, брандсбойты |
2.6.3. Истечение при переменном напоре
Рассмотрим истечение жидкости в атмосферу при переменном напоре через донное отверстие сосуда.
sdh = Qdt; sdh = m so  dt; dt =
dt; dt = 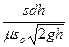 ,
,
где h – переменная высота уровня жидкости;
dh – изменение высоты жидкости за время dt.

Рис. Схема опорожнения сосуда
Найдем время полного опорожнения сосуда, проинтегрировав выражение dt = f (h):
T = 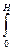
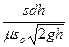 =
=  =
= 
 .
.
В полученном выражении в числителе – двойной объем сосуда, в знаменателе - расход жидкости в начальный момент истечения при напоре Н.
Вывод: время полного опорожнения сосуда в два раза больше, чем время истечения того же объема жидкости при постоянном напоре Н, равном первоначальному.
2.7. Кавитация в потоке жидкости
2.7.1. Физика явления
Рассмотрим трубу, имеющую зауженный участок.

Запишем уравнение Бернулли в давлениях для сечений 1-1 и 2-2, приняв за плоскость сравнения ось трубы:
р1 + rv1 2 /2 = р2 + rv2 2 /2 = р0 = const – полное давление
В узком сечении скорость резко увеличивается, т.е. увеличивается динамическое давление. Следовательно, статическое давление р уменьшается. Если абсолютное давление р уменьшается до давления насыщенного пара рн.п. , т.е. при р = рн.п. , возникает явление кавитации.
Кавитацией называется нарушение сплошности потока жидкости вследствие образования в ней пустот (пузырьков, пузырей, полостей), заполненных паром или газом. При снижении давления до давления насыщенного пара из жидкости выделяются ее пары и растворенные в ней газы. Сначала образуются кавитационные пузырьки, которые при заполнении их газами и парами растут. Они перемещаются потоком жидкости, увеличиваются в размерах, образуют круп-ные пузыри и полости.
Для воды при t = 20°С рн.п. = 2400 Па (для сравнения ратм = 101320 Па).
Кавитация – это холодное «кипение» жидкости. За зоной кавитации давление растет, рост пузырей прекращается и они мгновенно «схлопываются».
Запишем уравнение Бернулли в напорах для двух произвольных сечений потока реальной жидкости:
z1 + р1 /rg + av1 2 /2g = z2 + р2 /rg + av2 2 /2 + Shпот = Н = const.
Из уравнения видно, что снижение давления может произойти не только при увеличении скорости движения жидкости, но и по другим причинам. Например. при значительном увеличении геометрической высоты (при чрезмерном поднятии трубопровода), при больших потерях напора (если на трубопроводе много местных сопротивлений), что также может привести к кавитации.
Дата добавления: 2014-12-23; просмотров: 314; Мы поможем в написании вашей работы!; Нарушение авторских прав |