Коэффициент корреляции

Рассмотрим наиболее важный для практики и теории случай линейной зависимости.

На первый взгляд подходящим параметром тесноты связи по является коэффициент регрессии , ибо, он показывает, на сколько единиц в среднем изменится , когда увеличится на одну единицу.

Однако более тщательный анализ показывает несостоятельность выбора коэффициента на эту роль.

Во-первых, две корреляционные зависимости могут иметь одинаковые значения , то есть равные угловые коэффициенты прямых регрессии, но различную степень тесноты связи.

Во-вторых, коэффициент регрессии зависит от единиц измерения переменных.

Очевидно, что для «исправления» как показателя тесноты связи нужна стандартная системы единиц измерения, в которых данные по различным характеристикам оказались бы сравнимы между собой. Такой стандартной системой единиц является система, в которой в качестве единицы измерений переменной используется его среднее квадратическое отклонение .

Представим уравнение регрессии по (2.11) в эквивалентном виде

(3.1)

В этой системе величины

(3.2)

показывает, на сколько величин 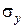изменится в среднем , когда увеличится на одно .

Величина 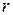является показателем тесноты связи и называется коэффициентом корреляции.

Нетрудно видеть, что 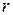совпадает по знаку с (а значит, и с ). Если , то корреляционная связь между переменными называется прямой, если – обратной. При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условного среднего значения другой.

Учитывая (2.12), формулу для 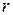представим в виде

(3.3)

Отсюда видно, что формула для 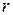симметрична относительно двух переменных, то есть переменные и можно менять местами. Тогда аналогично (3.2) можно записать

(3.4)

Найдя произведение обеих частей равенств (3.2) и (3.4) получим

(3.5)

или

(3.6)

то есть коэффициент корреляции 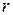переменных и есть среднее геометрическое коэффициентов регрессии, имеющее их знак.

Отметим другие модификации формулы для :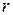

	(3.7)
	(3.8)

Для практических расчетов наиболее удобна формула (3.8), так как в ней 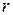находится непосредственно из данных наблюдений.

Рассмотрим основные свойства коэффициента корреляции (при достаточно большом объеме выборки ):

1. Коэффициент корреляции принимает значения на отрезке [-1,1], т.е.

(3.9)

В зависимости от того, насколько приближается к 1, различают связь слабую , умеренную , заметную , высокую и весьма высокую .

2. Если все значения переменных увеличить (уменьшить) на одно и то же число или в одно и то же число раз, то величина коэффициента корреляции не изменится.

3. При корреляционная связь представляет линейную функциональную зависимость. При этом линии регрессии по и по совпадают и все наблюдаемые значения переменных располагаются на общей прямой.

4. При линейная корреляционная связь отсутствует. При этом групповые средние переменных совпадают с их общими средними, а линии регрессии по и по параллельны осям координат. Равенство говорит лишь об отсутствии линейной корреляционной зависимости (некоррелированности переменных), но не вообще об отсутствии корреляционной, а тем более статистической зависимости.