Энергия взаимодействия в системе частиц

Для описания взаимодействия в приближении «дальнодействия» можно ввести еще одну специфическую энергетическую характеристику. Соответствующую величину называют энергией взаимодействия – е_вз. Для потенциальных сил ее можно рассматривать как обобщение ранее введенной потенциальной энергии. Потенциальная энергия – это характеристика воздействия на частицу со стороны другого, более массивного материального объекта, который мы принимаем за неподвижный. Она зависит от координат только более легкой частицы. Если же в задаче рассматриваются равноправные объекты, то придется учесть и отдачу второй частицы. Теперь мы имеем дело уже не с воздействием, а с взаимодействием, которое должно зависеть от взаимного расположения обоих объектов в данный момент времени. Поэтому энергия взаимодействия является функцией расстояния между объектами, т.е. при их перемещениях не остается постоянной. Важно подчеркнуть, что энергия взаимодействия не принадлежит отдельной частице. Это общая характеристика системы из двух частиц, как бы их общий «обменный фонд». Логично поставить вопрос, как скажется учет энергии взаимодействия на полной энергии системы частиц. Для ответа на него используем следующие рассуждения. Мы уже знаем, что при столкновениях равноправные частицы способны обмениваться долями импульса и энергии, причем в начале и конце процесса полная энергия системы, равная сумме энергий покоя и кинетических энергий, остается неизменной. В то же время нам известно, что для модели одной частицы, испытывающей потенциальное воздействие со стороны массивного неподвижного объекта, сохраняется механическая энергия, равная сумме кинетической и потенциальной энергий.

Рассмотренные выше ситуации можно расценивать как предельные случаи для модели системы взаимодействующих частиц. На этом основании можно предположить, что полная энергия в этой модели должна иметь черты, сходные с предельными. В результате энергия изолированной системы из двух частиц, мгновенно взаимодействующих друг с другом, принимает вид

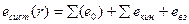(7.15).

где r – расстояние между двумя объектами, моделируемыми частицами, а суммирование производится по обеим частицам.

Эта величина со временем не изменяется. Хотя описание взаимодействия в этом приближении не является абсолютно точным, оно вполне применимо к системам типа планета-звезда, двухатомная молекула и электрон в атоме.

Как видно, модель системы взаимодействующих частиц является более сложной по сравнению с моделью свободных частиц, ведь в ней помимо привычных «индивидуальных» величин (типа энергий отдельных частиц) фигурирует и «коллективная» величина – энергия взаимодействия. Именно поэтому в последнем случае нельзя использовать модель системы свободных частиц. Она ведь не способна описать все нюансы поведения той реальной системы, где есть взаимодействие. Однако богатство теоретического арсенала физики иногда позволяет мысленно построить другую эквивалентную систему, которая имеет то же значение полной энергии, но состоит из свободных объектов. Конечно, это будут уже другие, придуманные частицы – их называют квазичастицами (частицеподобными объектами). Они, в принципе, могут иметь совершенно иные характеристики по сравнению с исходными – другие массы, заряды и т.п. Но если удается это исполнить, то картина их движения становится более простой и наглядной. Подобная модель называется моделью квазичастиц. На ее основе открывается возможность анализировать поведение более сложной системы.

Рассмотрим в связи с этим систему из двух движущихся частиц, которую можно моделировать как изолированную систему с энергией взаимодействия. На ее примере мы покажем, как можно в принципе вводить модель квазичастиц. Анализируя выражение для полной энергии системы, нетрудно видеть, что кинетические энергии частиц и энергия взаимодействия в нем зависят от времени – ведь каждая из частиц несвободна, и к тому же они движутся. Кроме того, из-за равноправного взаимодействия их движения не являются независимыми, и одно влияет на другое.

Однако в некоторых случаях удается сделать преобразования для энергии системы и добиться того, чтобы она представляла собой сумму энергий двух независимых движений. Возможность такого преобразования связана с тем, что система частиц в некотором роде подобна двойной звезде: при взгляде издалека она выглядит как единое целое, т.е. как одна частица, но при наблюдении в телескоп становятся заметны не только две звезды, но и их взаимные перемещения. Соответственно, эти типы движения называются поступательным и внутренним движениями. Для исходной системы в целом эти движения являются коллективными (в каждом из них частично участвует каждая из частиц). Но внешне все можно представить так, как будто мы имеем дело с независимыми движениями двух независимых частицепо-добных объектов или «квазичастиц». Их появление можно оправдать следующим образом.

При значительном удалении исходную систему можно рассматривать как некую новую единую частицу (квазичастицу), имеющую массу 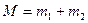и скорость

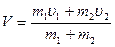(7.16).

Данная квазичастица имеет координаты и скорость центра масс системы, которая для исходной системы служит скоростью поступательного движения. Эту квазичастицу будем условно называть «центроном». Он совершает равномерное прямолинейное движение – ведь исходная система как целое изолирована.

Внутреннему движению будет соответствовать другая квазичастица – «интон». Ее масса это, так называемая, приведенная масса системы:

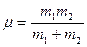(7.17).

Характер движения интона в разных конкретных случаях может быть различным, потому что он определяется конкретным типом взаимодействия. Но самое главное заключается в том, что интон сам по себе уже ни с кем не взаимодействует. Он соответствует модели несвободной частицы, находящейся под воздействием потенциальной силы, а потому обладает постоянной механической энергией.

Главный результат проведенных преобразований состоит в том, что в описанном случае полную энергию исходной системы можно представить в виде суммы энергий отдельных квазичастиц (центрона с массой М и интона с массой m):

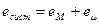.(7.18).

В этой сумме каждое слагаемое по разным причинам теперь уже не зависит от времени:

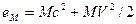(7.19).

как полная энергия свободной квазичастицы – центрона

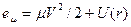(7.20).

как механическая энергия квазичастицы – интона.

Таким образом, исходная система представлена в виде системы квазичастиц, которые не взаимодействуют между собой – ведь энергия полученной вымышленной системы не содержит члена, ответственного за взаимодействие.

Изложенный выше подход к описанию взаимодействия является типичным для разных разделов физики. Его особая эффективность проявляется в системах взаимодействующих частиц, движение которых определяется малыми отклонениями от положения равновесия. Такие системы часто удается трактовать как совокупность независимых квазичастиц и в тех случаях, когда исходных частиц больше двух. Примером такой системы может служить линейная цепочка грузиков, устроенная следующим образом. С помощью упругих пружинок крайние грузики прикреплены к массивным стенкам, а внутренние связаны между собой. Но здесь следует учесть, что система грузиков не является свободной, а находится под воздействием упругих сил, которые обусловлены наличием пружин, прикрепленных к массивным стенкам. Поэтому в данной ситуации исходная система должна описываться моделью системы взаимодействующих частиц, которая сама испытывает внешнее воздействие. Если легко подтолкнуть один из грузиков, то система, в общем случае, будет совершать достаточно сложное движение, которому соответствует так называемая модель «связанных осцилляторов». Установить ее закономерности даже на визуальном уровне нелегко.

Если грузиков всего два, то к данной системе можно применить предыдущие рассуждения. Проведя необходимые преобразования, можно построить другую эквивалентную модель. Она сводится к системе двух независимых квазичастиц, которые как и прежде, можно назвать центроном и интоном. Первая квазичастица описывает поведение всей системы как целого, а вторая – ее внутреннее движение, при этом они имеют соответственно массы М и m. В отличие от предыдущей задачи, центрон в этом случае не является свободной частицей, а находится под воздействием некой эффективной упругой силы. Поэтому он описывается моделью гармонического осциллятора, т.е. совершает гармоническое колебание с частотой w_Ц. Интон, в свою очередь, также испытывает упругое воздействие, но с другим эффективным коэффициентом упругости, поэтому он также является гармоническим осциллятором, однако с другой частотой w_ин. Итак, в данном случае модель системы взаимодействующих частиц в виде связанных осцилляторов нам удалось заменить системой квазичастиц в виде невзаимодействующих осцилляторов.

Отметим, что в данном случае модель, состоящая из центрона и интона, допускает и другую интерпретацию, на основе которой может быть построена еще одна важная эквивалентная модель. Мы остановимся на ней более подробно, потому что она допускает далеко идущие обобщения. Дело в том, что колебания, соответствующие частотам w_Ц и w_ин, являются коллективными движениями системы. В них на самом деле участвуют обе исходные частицы, двигаясь совместно либо в одну сторону (синфазно, как в центроне), либо в разные стороны, попеременно то навстречу друг другу, то разбегаясь друг от друга (противофазно, как в интоне). С помощью определенных начальных условий можно возбудить в чистом виде один из этих типов совместного движения.

Рассматривая в отдельности каждое из этих взаимосогласованных колебаний, можно как бы забыть не только об исходных грузиках на пружинках, но даже и о совокупности квазичастиц «центрон + интон». Вместо них следует представить себе уже не локализованные частицы, а распределенную систему. Другими словами, совершить переход от корпускулярной модели к континуальной (заметим, что для двух грузиков такой переход несколько условен, но, как мы увидим позже, в системе из многих грузиков он вполне оправдан). В этом случае колебательное движение с частотой w_ин либо w_Ц исследует приписать всему континууму – для создания наглядного образа подобного движения говорят даже о «размазанном» осцилляторе. Каждый из этих возможных типов колебательного движения в континуальной системе по иному еще называют гармонической или нормальной модой. Поэтому можно сказать, что в данной системе возможны две гармонические моды – это синфазная с частотой w_Ц и противофазная с частотой w_ин, которые возбуждаются либо по отдельности, либо одновременно. Гармонические моды, по существу, это также своеобразные квазичастицы. С одной стороны, они независимы, потому что не взаимодействуют: энергию исходной системы можно представить строго в виде суммы энергий отдельных мод. С другой стороны, они очень специфичны, потому что не локализованы в пространстве, а размазаны по системе. В случае двух связанных осцилляторов, как говорилось выше, возможны оба эквивалентных подхода к моделированию. С одной стороны – введение индивидуальных локализованных квазичастиц (центрона и интона), имеющих определенные положения в пространстве и массы. С другой стороны – введение коллективных квазичастиц – гармонических мод, размазанных по системе в целом. При увеличении числа упруго взаимодействующих частиц подобная эквивалентность теряется. Индивидуальные квазичастицы с определенными массами ввести более не удается. В то же время исходную систему частиц по-прежнему можно представить совокупностью гармонических мод, в движении каждой из которых участвуют все исходные частицы. Примером такой системы может служить кристаллическая решетка. Поскольку атомов в одной регулярной цепочке очень много, а расстояния между ними малы, то гармонические моды представляют собой стоячие волны. Каждую из них можно трактовать как совокупность прошедшей и отраженной бегущих волн.

Область применения модели гармонической моды не ограничивается лишь системами частиц, связанных упругими взаимодействиями. Эта модель оказывается весьма эффективной в любых случаях, когда речь идет о малых колебаниях каких-либо величин или об их распространении в пространстве в виде волн., в частности,, произвольное электромагнитное излучение в модели континуума также может быть представлено как совокупность гармонических нормальных мод. При этом каждой моде соответствует одна из электромагнитных волн с определенной частотой, а электромагнитное излучение в целом – это суперпозиция независимых гармонических мод.

Контрольные вопросы:

1. Что в физике обозначает понятие «взаимодействие»?

2. Какие существуют типы взаимодействия?

3. Каковы характеристики контролируемого воздействия на частицу?

4. Назовите фундаментальные силы природы.

5. Какими будут значения положения и скорости частицы в некий последующий момент времени?

6. Опишите энергию взаимодействия в системе частиц.