
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Центральная предельная теорема.
Центральная предельная теорема теории вероятностей представляет собой совокупность предложений, устанавливающих условия возникновения нормального закона распределения.
Пусть на 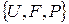 заданы независимые случайные величины
заданы независимые случайные величины 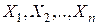 с числовыми характеристиками
с числовыми характеристиками

| (10.1.1) |
Рассмотрим случайные величины

| (10.1.2) |
и установим условия, при которых распределение случайной величины  с возрастанием п становится сколь угодно близким к нормальному N(0,1), т.е.
с возрастанием п становится сколь угодно близким к нормальному N(0,1), т.е. 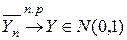 .
.
Будем говорить, что последовательность случайных величин 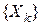 удовлетворяет центральной предельной теореме, если
удовлетворяет центральной предельной теореме, если 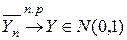 .
.
Заметим, что 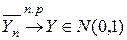 означает, что при достаточно большом n распределение Yn становится близким к нормальному
означает, что при достаточно большом n распределение Yn становится близким к нормальному 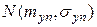 .
.
В самом деле, пусть 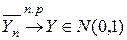 . Тогда для любого сколь угодно малого
. Тогда для любого сколь угодно малого 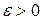 существует
существует 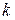 , что при
, что при 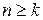 выполняется условие
выполняется условие
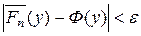
|
Здесь 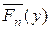 - функция распределения
- функция распределения  : Ф(y) - функция распределения
: Ф(y) - функция распределения 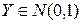 .
.
Положим 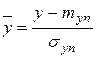 . Тогда для
. Тогда для 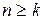 :
:
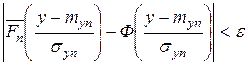
| (10.1.3) |
Поскольку
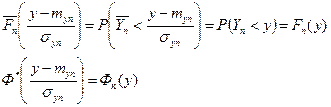
|
где 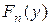 – распределение
– распределение 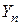 , а
, а 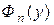 - распределение
- распределение 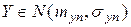 , то вместо (10.1.3) можно записать:
, то вместо (10.1.3) можно записать:
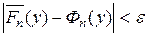
|
Случайную величину  , очевидно, можно представить в виде
, очевидно, можно представить в виде
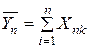
| (10.1.4) |
где  - независимые случайные величины с характеристиками
- независимые случайные величины с характеристиками
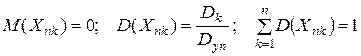
| (10.1.5) |
Если 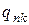 - характеристическая функция
- характеристическая функция 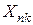 , то характеристическая функция
, то характеристическая функция 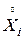 случайной величины
случайной величины  в силу независимости
в силу независимости  имеет вид:
имеет вид:
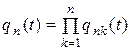
| (10.1.6) |
Теперь, учитывая теорему единственности, вопрос о 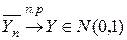 можно свести к установлению сходимости
можно свести к установлению сходимости
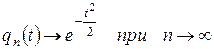
| (10.1.7) |
Этот прием будет основным в доказательстве следующей теоремы, дающей достаточное условие для 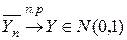 .
.
Дата добавления: 2014-12-23; просмотров: 162; Мы поможем в написании вашей работы!; Нарушение авторских прав |