Простая случайная бесповторная выборка

При оценке генеральных характеристик мы исходили из того, что выборка была произведена по схеме повторного случайного отбора. В случае бесповторной случайной выборки применяют те же формулы, что и для повторной выборки, но вычисление средних квадратических отклонений производится с поправочным коэффициентом.

. (1.26)

Оценка генеральной доли для бесповторной выборки есть .

Теорема. Выборочная доля бесповторной выборки есть несмещенная и состоятельная оценка генеральной доли , причем её дисперсия

. (1.27)

Доказательство. мМтематическое ожидание суммы равно сумме математических ожиданий слагаемых, поэтому и для бесповторной выборки М , т.е. - несмещённая оценка для

Рассмотрим теперь дисперсию бесповторной выборки:

.

Случайная величина m в случае бесповторной выборки имеет гипергеометрическое распределение и

Подставим его в (*), получим:

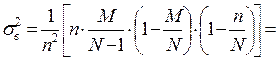
При , т.е. если объём выборки много меньше N, можно считать, что выборка практически не отличается от повторной и дисперсии их приближённо равны, т.е.

Если то выборочная доля будет совпадать с генеральной, и её дисперсия будет равна нулю.

Рассмотрим теперь оценку генеральной средней для бесповторной выборки.

Теорема: бесповторной выборки есть несмещенная и состоятельная оценка для генеральной средней , причем

(1.28)

Доказательство.Пусть X₁, X₂,…,X_k – зависимые случайные величины. все они распределены так же, как и в повторной выборке, с теми же частотами, что и в генеральной совокупности.

			…
			…

При этом E(x_i) = – генеральная дисперсия.

Обозначим

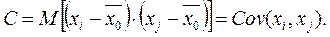(1.29)

Если , то С – генеральная дисперсия ( ),

Если , то С – ковариация (C = Cov(x_i,x_j)).

Выделим из слагаемых те n слагаемых, где , тогда

Пусть теперь объём выборки n = N, тогда x₁,x₂,…, x_n – не случайные величины, и дисперсия такой «выборки» D = 0, т.е. 0.

Отсюда . Подставим это в последнее. равенство

.

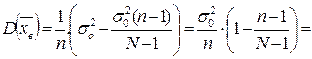
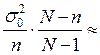
Теорема о несмещённости и состоятельности оценки генеральной средней и об оценке дисперсии бесповторной выборки полностью доказана.

Пример 1.22. Для определения доли стандартных изделий в партии, содержащей 2500 деталей, произвели случайную бесповторную выборку объёмом 400 деталей.Доля стандартных деталей в ней оказалась равной 0,95. Известно также, что при повторной выборке того же объёма среднеквадратичное отклонение составляло Найти доверительную вероятность, если допустимая погрешность при определении этой доли равна ±2%

Решение.По условию ;N= 2500;

. Найти .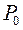

1)

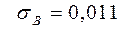
2)

3)

Пример 1.23. Выборочная совокупность объёмом 900 единиц является бесповторной и выделена из генеральной совокупности объемом 4500 единиц, при этом 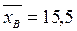. Определить доверительные границы при оценке генеральной средней, которые можно гарантировать с вероятностью 0,95.

Решение.По условию . Найти или .

1)

2) Так как , то по таблицам

3) .

Доверительные границы: 15,5 - 0,23 и 15,5 + 0,23, т.е.

Заметим, что ошибка приближенного равенства для бесповторной выборки может быть вычислена по формуле:

(1.30)