
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дослідження динамічних систем з дискретним часом
Процес, що має марківську властивість й описує ТС зі скінченним числом станів 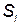 (
( 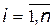 ), переходи в якому здійснюються у фіксовані моменти часу, називають дискретним марківським ланцюгом. При цьому кожному переходу відповідає перехідна ймовірність
), переходи в якому здійснюються у фіксовані моменти часу, називають дискретним марківським ланцюгом. При цьому кожному переходу відповідає перехідна ймовірність 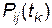 . Для кожного моменту часу переходи утворюють повну групу подій:
. Для кожного моменту часу переходи утворюють повну групу подій:
 , (3)
, (3)
де відповідно 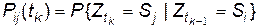 .
.
Взаємозв’язок між перехідними ймовірностями 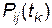 та ймовірностями станів
та ймовірностями станів 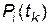 (ймовірностями того, що в момент часу
(ймовірностями того, що в момент часу  система знаходиться в стані
система знаходиться в стані 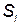 ) показано на рис. 2.
) показано на рис. 2.
Графічну модель можливих станів такої ТС можна умовно зобразити у вигляді орієнтованого графа станів. На такому графі кожному стану ТС ставиться у відповідність вершина графа, що з'єднується ребрами з іншими вершинами. Напрямки ребер відповідають напрямкам можливих переходів, а ймовірності переходів розглядаються як вага відповідних ребер.
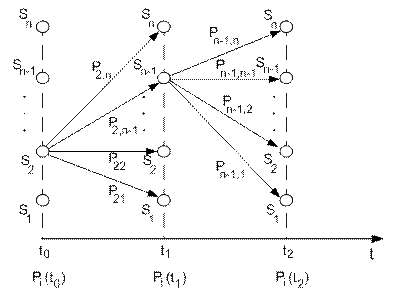
Рис. 2. Взаємозв’язок між перехідними ймовірностями 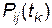
та ймовірностями станів 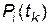
Приклад. Для оцінювання якості інтегральних мікросхем (ІМС) проводять вимірювання параметрів кожної з них автоматом контролю. Мікросхеми надходять до системи контролю послідовно, через рівні проміжки часу. Імовірність відхилення параметрів ІМС від допустимих значень становить 0,1. Якщо параметри трьох ІМС, що надходять послідовно, виходять за межі допустимих значень, то вся партія відбраковується. Зобразити граф станів системи і записати матрицю перехідних імовірностей.
Визначимо стані системи контролю якості: 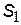 – параметри ІМС знаходяться у межах допустимих значень;
– параметри ІМС знаходяться у межах допустимих значень;  – параметри однієї ІМС виходять за межі допустимих значень;
– параметри однієї ІМС виходять за межі допустимих значень;  – параметри двох ІМС, що надходять послідовно, виходять за межі допустимих значень;
– параметри двох ІМС, що надходять послідовно, виходять за межі допустимих значень;  – параметри трьох ІМС, що надходять послідовно, виходять за межі допустимих значень – партія відбраковується.
– параметри трьох ІМС, що надходять послідовно, виходять за межі допустимих значень – партія відбраковується.
Оскільки надходження мікросхем відбувається через рівні проміжки часу, то система контролю якості переходить зі стану в стан у строго фіксовані моменти часу, що дає можливість досліджувати систему за допомогою дискретних марківських ланцюгів.
У початковий момент часу система перебуває в стані 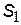 . При надходженні чергової ІМС система з імовірністю 0,1 перейде в стан
. При надходженні чергової ІМС система з імовірністю 0,1 перейде в стан  і з імовірністю 0,9 залишиться у початковому стані, тому що
і з імовірністю 0,9 залишиться у початковому стані, тому що
 .
.
 Надходить друга ІМС. Система з імовірністю 0,1 перейде в стан
Надходить друга ІМС. Система з імовірністю 0,1 перейде в стан  . Якщо всі параметри ІМС виявляться в межах допустимих значень, то система повернеться в стан
. Якщо всі параметри ІМС виявляться в межах допустимих значень, то система повернеться в стан 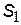 з імовірністю 0,9 (відповідно до виразу 3).
з імовірністю 0,9 (відповідно до виразу 3).
Далі надходить третя ІМС, і з імовірністю 0,1 система переходить у стан  (партія відбраковується) або з імовірністю 0,9 – у стан
(партія відбраковується) або з імовірністю 0,9 – у стан 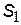 .
.
Граф станів системи зображено на рис. 3, відповідно до якого матрицю перехідних імовірностей можна записати як
 .
.
Дискретний марківський ланцюг називають однорідним, якщо перехідні ймовірності не залежать від номера переходу, тобто 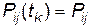 , і він повністю описується:
, і він повністю описується:
- вектором початкового стану
 ,
,
елементи якого характеризують імовірності того, що в початковий момент часу система перебуває в стані 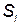 (
( 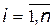 ), і відповідають виразу (1);
), і відповідають виразу (1);
- матрицею переходів
 ,
,
у якій імовірності, розташовані за головною діагоналлю матриці, відповідають тому, що система стану не змінила; при  ймовірності відповідають неможливим переходам системи; при
ймовірності відповідають неможливим переходам системи; при 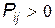 – можливим переходам системи зі стану
– можливим переходам системи зі стану  у стан
у стан  .
.
Матриця переходів є стохастичною, тобто
 (
( 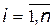 ) за умови, що
) за умови, що  (4)
(4)
Зазвичай вважають, що дискретний марківський ланцюг описує перехідний режим роботи ТС на рівних інтервалах часу. Отже, k-й ступінь матриці переходів можна розглядати як матрицю переходів за 
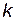 кроків (так само, як під час дослідження статичних ТС), тобто розподіл ймовірностей станів системи після k кроків (абсолютні ймовірності) визначається виразом
кроків (так само, як під час дослідження статичних ТС), тобто розподіл ймовірностей станів системи після k кроків (абсолютні ймовірності) визначається виразом
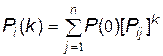 , (5)
, (5)
де k – кількість розглянутих кроків; 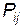 – імовірність переходу системи зі стану
– імовірність переходу системи зі стану  у стан
у стан  , визначена відповідною матрицею переходів;
, визначена відповідною матрицею переходів;  – вектор початкового стану.
– вектор початкового стану.
Дискретний марківський ланцюг називають неоднорідним, якщо перехідні ймовірності змінюються зі зміною номера переходу, тобто  , і для його опису необхідні:
, і для його опису необхідні:
- k матриць перехідних імовірностей 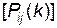 , де k – кількість кроків, що розглядаються;
, де k – кількість кроків, що розглядаються;
- вектор початкового розподілу ймовірностей.
Матриця 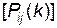 є стохастичною, має властивість (4) і тільки невід'ємні елементи:
є стохастичною, має властивість (4) і тільки невід'ємні елементи:  .
.
Якщо під час аналізу динамічної ТС, поводження якої описується однорідним дискретним марківським ланцюгом, необхідно розглянути її поводження на короткому інтервалі часу, то абсолютні ймовірності слід обчислювати відповідно до виразу (5). Однак найважливіше вивчити поводження системи на великому інтервалі часу, тобто в умовах, коли число переходів прямує до нескінченності. У цьому випадку, наведений вище метод є непридатним; потрібен систематичний підхід, що дає можливість прогнозувати довгострокове поводження системи. Введемо такі означення.
Ланцюг Маркова називають незвідним ланцюгом (або ергодичним), якщо будь-який стан  можна досягти з будь-якого іншого стану
можна досягти з будь-якого іншого стану  за скінченне число переходів, тобто при
за скінченне число переходів, тобто при 
 для
для 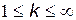 . У цьому випадку всі стани ланцюга називають сполученими. Множину станів ланцюга Маркова
. У цьому випадку всі стани ланцюга називають сполученими. Множину станів ланцюга Маркова 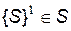 називають замкненою, якщо система, що принаймні один раз перебувала в одному зі станів цієї множини, буде перебувати в множині
називають замкненою, якщо система, що принаймні один раз перебувала в одному зі станів цієї множини, буде перебувати в множині  протягом нескінченного інтервалу часу. Умова ергодичності однорідного марківського ланцюга – всі її стани є сполученими, а орієнтований граф, що описує функціонування системи, є сильнозв’язним.
протягом нескінченного інтервалу часу. Умова ергодичності однорідного марківського ланцюга – всі її стани є сполученими, а орієнтований граф, що описує функціонування системи, є сильнозв’язним.
Властивість ергодичних марківських ланцюгів: при досить великій кількості k (  настає стаціонарний режим, при якому ймовірності
настає стаціонарний режим, при якому ймовірності  станів майже не залежать від часу й розподілу ймовірностей у початковий момент часу, тобто
станів майже не залежать від часу й розподілу ймовірностей у початковий момент часу, тобто 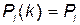 .
.
Вектор  називають вектором стаціонарних (фінальних) імовірностей, кожний компонент якого характеризує середню частку часу, протягом якого система перебуває в стані, що розглядається.
називають вектором стаціонарних (фінальних) імовірностей, кожний компонент якого характеризує середню частку часу, протягом якого система перебуває в стані, що розглядається.
Для визначення стаціонарних імовірностей  перебування системи в стані
перебування системи в стані 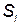 потрібно скласти систему з
потрібно скласти систему з 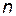 лінійних рівнянь виду
лінійних рівнянь виду
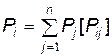 ,
, 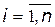 ,
,
причому значення ймовірностей  мають відповідати умові (1).
мають відповідати умові (1).
Окремим випадком замкненої множини є стан  , якому у матриці переходів відповідає рядок, у якому всі перехідні ймовірності
, якому у матриці переходів відповідає рядок, у якому всі перехідні ймовірності  , крім перехідної ймовірності
, крім перехідної ймовірності  . У цьому випадку стан
. У цьому випадку стан  називають поглинальним.
називають поглинальним.
| Приклад | Розглянемо ланцюг Маркова із прикладу. Як видно з рис. 3, всі стани системи не становлять незвідний харківський ланцюг, оскільки станів 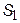 , , 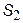 і і 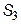 не можна досягти зі стану не можна досягти зі стану 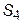 . Стан . Стан 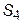 утворює замкнену множину й, таким чином, є поглинальним з перехідною ймовірністю утворює замкнену множину й, таким чином, є поглинальним з перехідною ймовірністю  . На графі такому стану відповідає тупикова вершина. Можна також стверджувати, що стан . На графі такому стану відповідає тупикова вершина. Можна також стверджувати, що стан 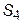 відповідає ергодичному марківському ланцюгу. відповідає ергодичному марківському ланцюгу.
|
Усі стани ергодичного марківського ланцюга мають утворювати замкнену множину, і жодна підмножина цієї множини не може бути замкненою. Замкнена множина  задовольняє всім умовам, що характеризують марківський ланцюг, і, отже, її можна незалежно аналізувати.
задовольняє всім умовам, що характеризують марківський ланцюг, і, отже, її можна незалежно аналізувати.
Очевидно, що повну множину станів системи  можна розбити на замкнені підмножини (класи)
можна розбити на замкнені підмножини (класи)  ,
, 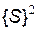 , …,
, …, 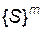 (
(  ,
, 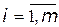 ) сполучених станів. При цьому до одного класу належать усі сполучені між собою стани. Стани, що належать різним класам, не є сполученими. Між класами існує ієрархічна залежність, зумовлена допустимими напрямками переходів з одного класу станів у інший.
) сполучених станів. При цьому до одного класу належать усі сполучені між собою стани. Стани, що належать різним класам, не є сполученими. Між класами існує ієрархічна залежність, зумовлена допустимими напрямками переходів з одного класу станів у інший.
Якщо перехід  є можливим, то зворотний перехід
є можливим, то зворотний перехід  є неможливим (оскільки у противному випадку знайшлася б пара сполучених станів, які належать різним класам, що суперечить правилу утворення класів). При цьому вважається, що клас
є неможливим (оскільки у противному випадку знайшлася б пара сполучених станів, які належать різним класам, що суперечить правилу утворення класів). При цьому вважається, що клас  знаходиться вище класу
знаходиться вище класу  в ієрархії класів. Класи сполучених станів можуть утворити одну або кілька ієрархій. У кожній з них клас, що займає останню (нижню) сходинку, називають ергодичною множиною станів, а інші класи – безповоротними множинами.
в ієрархії класів. Класи сполучених станів можуть утворити одну або кілька ієрархій. У кожній з них клас, що займає останню (нижню) сходинку, називають ергодичною множиною станів, а інші класи – безповоротними множинами.
| Примітка | Оскільки процес переходів системи з одного стану в інший не накладає ніяких обмежень на порядок нумерації станів і класів станів, класи прийнято нумерувати, починаючи з ергодичних множин і далі – в порядку зростання старшинства класів  , ,  , …, , …,  . Стани системи нумерують числами натурального ряду спочатку в першій ергодичній множині . Стани системи нумерують числами натурального ряду спочатку в першій ергодичній множині  , потім – в другому класі , потім – в другому класі  і так далі до останнього стану класу і так далі до останнього стану класу  (послідовність нумерації всередині класів значення не має). При такій нумерації перехід системи з одного класу станів в інший завжди пов'язаний зі зменшенням номера стану. (послідовність нумерації всередині класів значення не має). При такій нумерації перехід системи з одного класу станів в інший завжди пов'язаний зі зменшенням номера стану.
|
У зв’язку з цим стан  називають поворотним, якщо ймовірність того, що система, вийшовши із цього стану, повернеться в нього за скінченне число кроків хоча б один раз, дорівнює одиниці. Стан
називають поворотним, якщо ймовірність того, що система, вийшовши із цього стану, повернеться в нього за скінченне число кроків хоча б один раз, дорівнює одиниці. Стан  називають безповоротним, якщо ця ймовірність менша за одиницю. Стани, які належать ергодичним множинам, є поворотними, всі інші – безповоротними.
називають безповоротним, якщо ця ймовірність менша за одиницю. Стани, які належать ергодичним множинам, є поворотними, всі інші – безповоротними.
Ланцюги з безповоротними множинами складаються тільки з ергодичних множин. Якщо цих множин декілька, то між ними не може бути ніяких переходів, а отже, вони являють собою декілька незалежних, ізольованих марківських ланцюгів, що можуть вивчатися окремо. У ланцюгах з безповоротними множинами рух відбувається в напрямку до ергодичних множин, і зрештою ланцюг потрапляє в одну з них. Розглянемо поводження ланцюга в безповоротній множині.
До настання стаціонарного режиму в системі має місце перехідний процес, тривалість якого задається величиною
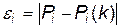 .
.
При  ,
,  режим у системі вважають незмінним (стаціонарним).
режим у системі вважають незмінним (стаціонарним).
Поводження системи в ергодичній множині досліджується так само, як і поводження ергодичних ланцюгів. А це означає, що можна обмежитися розглядом тільки поглинальних ланцюгів – ланцюгів, де всі ергодичні стани є поглинальними. Таким чином, усе різноманіття однорідних марківських ланцюгів з дискретним часом можна вивчити, застосовуючи прийоми дослідження поглинальних і ергодичних ланцюгів.
Дата добавления: 2015-01-01; просмотров: 141; Мы поможем в написании вашей работы!; Нарушение авторских прав |