Структурна компактність ТС

Під час оцінювання параметрів структурної компактності вводять параметр , що відображує близькість елементів один до одного, тобто мінімальну довжину шляху між вершинами 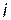і 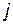. Для оцінювання параметра можна використовувати:

- матрицю суміжності , якщо не має додаткових даних про граф системи;

- матрицю 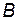, що виражає не тільки взаємозв'язок вершин, але й пропускну здатність ребер структури системи;

- матрицю довжин ребер .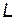

Для позначення ємності або інших подібних параметрів ребер графа системи використовується матриця 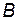. Наприклад, має місце граф вигляду з позначеними пропускними здатностями ребер (рис. 3). Виразимо елементи 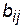матриці 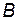у значеннях пропускної здатності:

. (8)

Очевидно, що порядок матриці 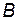, як і матриці суміжності, дорівнює N. Рядки матриці 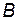містять інформацію про зв'язки кожної вершини графа ТС: перший рядок – про зв'язки першої вершини, другий рядок – про зв'язки другої вершини і т.д. Її половини, відділені нульовою діагоналлю, містять однакову інформацію. Тому квадратну матрицю (8) можна замінити трикутною:

.

Слід також зазначити, що для повнозв’язної структури всі елементи матриці 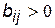, крім елементів головної діагоналі.

Топологічні властивості системи зручно виражати матрицею довжин ребер 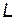. Матриця 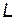складається за тими ж правилами, що і попередні. Діагональні її елементи (лівої діагоналі) дорівнюють нулю, тому що довжина ребра всередині вершини береться 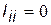. Якщо безпосереднього зв'язку між вершинами немає, то . Для структури системи, наведеної на рис. 4, матриця довжин ребер має такий вигляд:

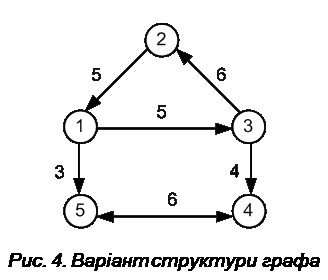
. (9)

Як і в матриці 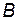, усі елементи матриці 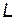для повнозв’язної структури 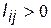, а .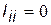

Слід мати на увазі, що елементи матриць 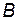і 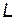можуть виражати не тільки ті фізичні параметри, які взято за основу під час їх складання (ємність і довжина ребер), але й інші фізичні характеристики. Так, елемент 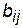може мати такий фізичний зміст: кількість каналів і транзитних ділянок цього шляху, швидкість передачі інформації, ефективно передана смуга частот, числове значення показників вірогідності, надійності, живучості та ін. Такі тлумачення мають місце й для елемента .

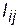Оцінювання структурної компактності (мінімальна довжина шляху між вершинами) полягає у визначенні найкоротших шляхів від усіх вершин до деякої вершини n у неповнозв’язній структурі ТС.

Довжина найкоротших шляхів визначається таким чином. Вага виділеної вершини 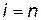береться такою, що дорівнює нулю ( 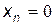). Вага кожної з вершин, що є сусідніми з вершиною n, визначається за виразом

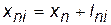при 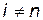, , 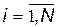(10)

де – довжина шляху між сусідніми вершинами (довжина ребра); N – кількість вершин графа.

При цьому елемент структури, що містить три вершини, послідовно з'єднані одна з одною, називають транзитною ланкою, а середню вершину цієї ланки – транзитною вершиною. Отже, як параметр може бути довжина шляху між вершиною n і вершиною i або кількість транзитів між цими вершинами. В останньому випадку, якщо вершини n та i – несусідні, параметр 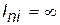, якщо n та i – сусідні, то параметр .

Виконавши обчислення за формулою (10), знайдемо мінімальне значення ваги:

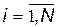, . (11)

Це мінімальна довжина шляху від вершини n до вершини i, тобто показник структурної компактності .

Прийнявши обчислені значення 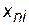за вагу вершин i, зробимо аналогічні обчислення для визначення ваги вершин, сусідніх з кожною з вершин i і далі, усе більш віддаляючись від вихідної вершини n. Результати обчислень заносять до так званої дистанційної таблиці, що являє собою модернізовану матрицю довжин ребер .

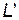Структурну компактність знайдемо за формулою

, (12)

де 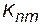– мінімальна довжина шляху між вершинами n і m; 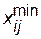– мінімальна довжина шляху між вершинами i та j, що утворюють шлях від вершини n до вершини m.

Приклад.Для структури системи, зображеної на рис. 4, оцінити компактність між вершинами 2 і 5.

Відповідно до виразу (10) обчислимо довжину шляху між вершиною 2 та сусідніми з нею вершинами, скориставшись матрицею довжини ребер (9):

, ,

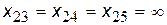тобто згідно з виразом (11) мінімальний шлях проходить через вершину 1:

.

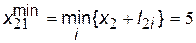Обчислимо довжину шляху між вершиною 1 та сусідніми з нею вершинами:

, , .

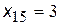Відповідно до виразу (11) мінімальний шлях становить

.

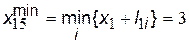Таким чином, згідно з виразом (12) мінімальна довжина шляху між вершинами 2 і 5 буде

.

Якщо відомо матрицю зв’язності , то цей метод обчислення мінімальної кількості транзитів можна суттєво спростити, застосувавши модернізовану матрицю 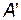. Суть модернізації матриці полягає в тому, що її елементи 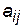, які позначають зв’язність несусідніх вершин, беруться такими, що дорівнюють не 0, а ¥.

Так, наприклад, для структури системи, зображеної графом G[5,7] (див. рис. 4), модернізована матриця зв’язності має такий вигляд:

. (13)

Для визначення шляху з мінімальною кількістю транзитів між будь-якою парою вершин n і m слід почленно додати елементи n-го рядка і m-го стовпця матриці 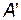(знайти 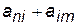) і визначити мінімальне значення суми.

Відповідно до цього правила індекси елементів, що входять до мінімальної суми, визначають номери вершин, що утворюють шлях з мінімальною кількістю транзитів.

Приклад.Для структури системи, зображеної на рис. 5, знайти мінімальний шлях між вершинами 2 і 5.

Відповідно до наведеного вище правила для визначення мінімальної кількості транзитів між вершинами 2і 5підсумуємо елементи другого рядка і п'ятого стовпця матриці 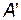, тобто знайдемо таку суму:

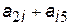при ,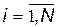

звідки , , .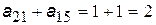

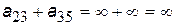Із отриманих значень суми 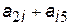вибираємо найменше: 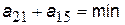. У цьому випадку за отриманою послідовністю індексів елементів, що входять до цієї суми, визначаємо номери вершин, які утворюють шлях з мінімальною кількістю транзитів між вершинами 2 і 5: шлях проходить через першу вершину. При цьому кількість транзитних вершин дорівнює двом.

Це легко перевірити. Складемо всі можливі шляхи між вершинами 2 і 5 і визначимо кількість транзитів між ними:

1-й шлях: 2-1-5, кількість транзитів – 2;

2-й шлях: 2-1-3-4-5, кількість транзитів – 4.

Зазначимо, що отримані результати не суперечать результатам, отриманим у попередньому прикладі.

Якщо довжина мінімального шляху більше двох, то для оцінювання параметрів структурної компактності використовують матричний метод або метод В.Г. Лазарєва. Цей метод потребує знання структури всієї технічної системи. За його допомогою можна отримати всі значення для заповнення дистанційної таблиці.