КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Электростатика
Краткая теория
· Закон сохранения заряда: в изолированной системе алгебраическая сумма зарядов всех частиц остается неизменной:
.
· Закон Кулона. Сила 
взаимодействия двух неподвижных точечных зарядов q1 и q2 прямо пропорциональна величине каждого заряда и обратно пропорциональна квадрату расстояния r между ними:
, или 
,
где значение коэффициента k в СИ равно 
; 
– электрическая постоянная, e – диэлектрическая проницаемость среды.
· Диэлектрическая проницаемость среды e показывает, во сколько раз взаимодействие зарядов в среде ослабляется по сравнению с вакуумом:
, или 
,
где F – сила взаимодействия зарядов в среде, F0 – в вакууме; E – напряжённость поля в среде, E0 – в вакууме.
· Напряженность электрического поля равна силе, действующей на единичный точечный положительный пробный заряд q, помещенный в данную точку поля:
.
· Сила, действующая на точечный заряд q, помещенный в электрическое поле
.
· Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда
.
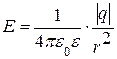· Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:
а) внутри сферы (r<R) E=0;
б) на поверхности сферы (r=R) 
;
в) вне сферы (r>R) 
.
Здесь e – диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
· Принцип суперпозиции (наложения) электрических полей: напряженность 
результирующего электрического поля, создаваемого несколькими источниками в некоторой точке пространства, равна геометрической сумме напряженностей полей 
, созданных в данной точке каждым источником в отдельности, причем каждая составляющая не зависит от наличия остальных полей:
.
В случае двух электрических полей с напряженностям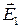и 
и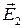 
модуль результирующего вектора напряженности (рис.6.1):
,
где a – угол между векторам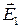и и 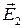(рис.4.1).
· Поверхностная плотность заряда, распределенного по поверхности, есть величина, равная заряду, приходящемуся на единицу площади поверхности:
.
· Линейная плотность заряда, распределенного по нити, есть величина, равная заряду, приходящемуся на единицу её длины:
.
· Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью
,
где s – поверхностная плотность заряда.
· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью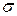 
заряда (поле плоского конденсатора)
.
Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.
· Потенциал электрического поляв данной точке равен отношению потенциальной энергии, которой обладает положительный точечный заряд, помещенный в данную точку поля, к величине этого заряда:
.
Иначе: потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность, к этому заряду:
.
Потенциал электрического поля в бесконечности условно принят равным нулю.
· Работа сил электрического поля при перемещении точечного заряда q из точки с потенциалом 
в точку с потенциалом 
:
.
Для однородного поля A=q∙E∙l∙cosa, где l – перемещение; a – угол между направлениями вектора и перемещения 
.
· Потенциал поля, созданного уединенным точечным зарядом 
на расстоянии 
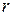от заряда, равен
.
· Потенциал электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:
внутри сферы (r<R) 
;
на поверхности сферы (r=R)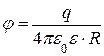 
;
вне сферы (r>R) .
Здесь e – диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
· Принцип суперпозиции: потенциал результирующего поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов полей, созданных в данной точке каждым из зарядов:
.
· Энергия W взаимодействия системы N точечных зарядов q1, q2, ..., qN определяется работой, которую эта система зарядов может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой
,
где 
– потенциал поля, создаваемого всеми (N–1) зарядами (за исключением i-го) в точке, где расположен заряд qi.
· Связь напряжённости и потенциала. В случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению
,
где j1 и j2 – потенциалы точек двух эквипотенциальных поверхностей; d – расстояние между этими поверхностями вдоль электрической силовой линии.
· Электрическая емкость уединенного проводника
,
где q – заряд, сообщенный проводнику; φ – потенциал проводника.
· Электрическая ёмкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью ε
.
Если сфера полая и заполнена диэлектриком, то электроемкость её от этого не изменяется.
· Емкость конденсатора определяется отношением модуля заряда q на одной обкладке к разности потенциалов U между обкладками:
.
· Электрическая емкость плоского конденсатора
,
где S – площадь пластин (каждой пластины); d – расстояние между ними; ε – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.
· Электрическая емкость С последовательно соединенных конденсаторов в общем случае (N – число конденсаторов)
.
В случае двух конденсаторов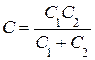 
.
В случае п одинаковых конденсаторов с электроемкостью С1 каждый
.
· Электрическая емкость параллельно соединенных конденсаторов в общем случае
C=C1+C2+...+CN.
В случае N одинаковых конденсаторов с электроемкостью С1 каждый:
C=N∙C1.
· Энергия заряженного проводника выражается через заряд q, потенциал φ и электрическую емкость С проводника следующими соотношениями:
.
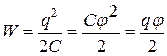· Энергия заряженного конденсатора
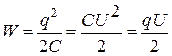
где С – электрическая емкость конденсатора, q – его заряд, U – разность потенциалов на его пластинах.
· Объемная плотность энергии – это энергия единицы объема:
.
· Объемная плотность энергии электростатического поля напряжённостью Е равна:
.
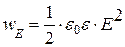Дата добавления: 2014-10-31; просмотров: 261; Мы поможем в написании вашей работы!; Нарушение авторских прав |