Формула последовательных испытаний Бернулли

Определение и свойства функции

Распределения случайной величины.

1. Определение функции распределения:

Функция распределения н.с.в. имеет вид

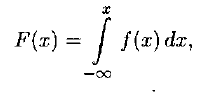
2. Свойства функции распределения:

Определение и свойства плотности

Распределения случайной величины

Определение и свойства математического ожидания и дисперсии случайной величины.

Дисперсия характеризует разброс значений случайной величины X относительно её математического ожидания.

Для дискретной случайной величины:

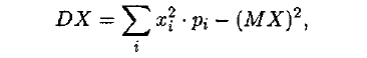
Для непрерывной случайной величины:

Плотность распределения и числовые

Характеристики нормального закона

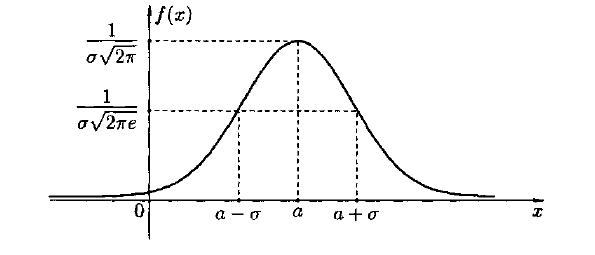
Функция распределения имеет вид

И называется функцией Гаусса.

Дата добавления: 2015-01-19; просмотров: 90; Нарушение авторских прав