
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие об игровых моделях. Платежная матрица. Нижняя и верхняя цена игры.
Теория игр представляет собой математическую дисциплину, предметом исследования которой являются методы принятия решения в конфликтных ситуациях.
Ситуация называется конфликтной, если в ней сталкиваются интересы нескольких (обычно двух) лиц, преследующих противоположные цели. Каждая из сторон может проводить ряд мероприятий для достижения своих целей, причем успех одной стороны означает неудачу другой.
В экономике конфликтные ситуации встречаются очень часто (взаимоотношения между поставщиком и потребителем, покупателем и продавцом, банкиром и клиентом). Конфликтные ситуации встречаются и во многих других областях.
Конфликтная ситуация порождается различием интересов партнеров и стремлением каждого из них принимать оптимальные решения, которые реализуют поставленные цели в наибольшей степени. При это каждому приходится считаться не только со своими целями, но и с целями партнера, и учитывать неизвестные заранее решения, которые партнеры будут принимать.
Обычно конфликтные ситуации трудны для непосредственного анализа благодаря множеству второстепенных приходящих факторов. Для того чтобы сделать возможным математический анализ конфликтной ситуации, ее необходимо упростить, учтя только основные факторы. Упрощенная формализованная модель конфликтной ситуации называется игрой, стороны, участвующие в конфликте, - игроками, а исход конфликта - выигрышем. Как правило, выигрыш (или проигрыш) может быть задан количественно; например, можно оценить проигрыш нулем, выигрыш - единицей, а ничью - 1/2.
Игра представляет собой совокупность правил, описывающих поведение игроков. Каждый случай разыгрывания игры некоторым конкретным образом от начала до конца представляет собой партию игры. Выбор и осуществление одного из предусмотренных правилами действий называется ходом игрока. Ходы могут быть личными и случайными. Личный ход - это сознательный выбор игроком одного из возможных действий (например, ход в шахматной игре).Случайный ход - это также выбор одного из множества вариантов, но здесь вариант выбирается не игроком, а некоторым механизмом случайного выбора (бросание монет, выбор карты из перетасованной колоды).
Стратегией игроканазывается совокупность правил, определяющих выбор его действий при каждом личном ходе в зависимости от сложившейся ситуации.
Если игра состоит только из личных ходов, то исход игры определен, если каждый из игроков выбрал свою стратегию. Однако если в игре имеются случайные ходы, то игра будет носить вероятностный характер и выбор стратегий игроков еще не определит окончательно исход игры.
Для того чтобы решить игру, или найти решение игры, следует для каждого игрока выбрать стратегию, которая удовлетворяет условию оптимальности, т.е. один из игроков должен получать максимальный выигрыш, когда второй придерживается своей стратегии. В то же время второй игрок должен иметьминимальный проигрыш, если первый придерживается своей стратегии. Такие стратегии называются оптимальными. Оптимальные стратегии должны удовлетворять условию устойчивости, т.е. любому из игроков должно быть невыгодно отказаться от своей стратегии в этой игре.
Целью теории игр является определение оптимальной стратегии для каждого игрока.
Рассмотрим парную конечную игру. Пусть игрок А располагает m личными стратегиями, которые обозначим A1, A2, ..., Am. Пусть у игрока В имеется n личных стратегий, обозначим их B1, B2, ..., Bm. Говорят, что игра имеет размерность m × n. В результате выбора игроками любой пары стратегий
Ai и Bj (i = 1, 2, ..., m; j = 1, 2, ..., n)
однозначно определяется исход игры, т.е. выигрыш aij игрока А (положительный или отрицательный) и проигрыш (- aij ) игрока В. Предположим, что значения о,у известны для любой пары стратегий (Ai ,Bj ). Матрица P = (aij ), i = 1, 2, ..., m; j = 1, 2, ..., n, элементами которой являются выигрыши, соответствующие стратегиям Ai и Bj , называется платежной матрицей или матрицей игры. Общий вид такой матрицы представлен в таблице 3.1.
Таблица 3.1

Строки этой таблицы соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В. Составим платежную матрицу для следующей игры.
Рассмотрим игру m × n с матрицей P = (aij ), i = 1, 2, ..., m; j = 1, 2, ..., n и определим наилучшую среди стратегий A1, A2, ..., Am. Выбирая стратегию Ai игрок А должен рассчитывать, что игрок В ответит на нее той из стратегий Bj , для которой выигрыш для игрока А минимален (игрок В стремится "навредить" игроку А). Обозначим через αi , наименьший выигрыш игрока А при выборе им стратегии Ai для всех возможных стратегий игрока В (наименьшее число в i-й строке платежной матрицы), т.е.

| (3.1) |
Среди всех чисел αi (i = 1, 2, ..., m) выберем наибольшее: . Назовем α нижней ценой игры, или максимальным выигрышем (максимином). Это гарантированный выигрыш игрока А при любой стратегии игрока В. Следовательно,

| (3.2) |
Стратегия, соответствующая максимину, называется максиминной стратегией. Игрок В заинтересован в том, чтобы уменьшить выигрыш игрока А; выбирая стратегию Bj , он учитывает максимально возможный при этом выигрыш для А. Обозначим

| (3.3) |
Среди всех чисел Bj ; выберем наименьшее и назовем β верхней ценой игры или минимаксным выигрышем (минимаксом). Это гарантированный проигрыш игрока В. Следовательно,

| (3.4) |
Стратегия, соответствующая минимаксу, называется минимаксной стратегией. Принцип, диктующий игрокам выбор наиболее "осторожных" минимаксной и максиминной стратегий, называется принципом минимакса. Этот принцип следует из разумного предположения, что каждый игрок стремится достичь цели, противоположной цели противника. Определим нижнюю и верхнюю цены игры и соответствующие стратегии в задаче.
Если верхняя и нижняя цены игры совпадают, то общее значение верхней и нижней цены игры α = β = v называется чистой ценой игры, или ценой игры. Минимаксные стратегии, соответствующие цене игры, являютсяоптимальными стратегиями, а их совокупность — оптимальным решением, или решением игры. В этом случае игрок А получает максимальный гарантированный (не зависящий от поведения игрока В) выигрыш v, а игрок В добивается минимального гарантированного (вне зависимости от поведения игрока А) проигрыша v. Говорят, что решение игры обладает устойчивостью, т.е. если один из игроков придерживается своей оптимальной стратегии, то для другого не может быть выгодным отклоняться от своей оптимальной стратегии.
Пара чистых стратегий Ai и Bj дает оптимальное решение игры тогда и только тогда, когда соответствующий ей элемент aij , является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация, если она существует, называется седловой точкой (по аналогии с поверхностью седла, которая искривляется вверх в одном направлении и вниз — в другом).
Основные понятия модели управления запасами.
Как в бизнесе, так и в производстве обычно принято поддерживать разумный запас материальных ресурсов или комплектующих для обеспечения непрерывности производственного процесса. Традиционно запас рассматривается как неизбежные издержки, когда слишком низкий его уровень приводит к дорогостоящим остановкам производства, а слишком высокий – к «омертвлению» капитала. Задача управления запасами – определить уровень запаса, который уравновешивает два упомянутых крайних случая.
Рассмотрим основные характеристики моделей управления запасами.
Спрос. Спрос на запасаемый продукт может быть детерминированным (в простейшем случае - постоянным во времени) или случайным. Случайность спроса описывается либо случайным моментом спроса, либо случайным объемом спроса в детерминированные или случайные моменты времени.
Пополнение склада. Пополнение склада может осуществляется либо периодически через определенные интервалы времени, либо по мере исчерпания запасов, т.е. снижения их до некоторого уровня.
Объем заказа. При периодическом пополнении и случайном исчерпании запасов объем заказа может зависит от того состояния, которое наблюдается в момент подачи заказа. Заказ обычно подается на одну и ту же величину при достижении запасом заданного уровня - так называемой точки заказа.
Время доставки. В идеализированных моделях управления запасами предполагается, что заказанное пополнение доставляется на слад мгновенно. В других моделях рассматривается задержка поставок на фиксированный или случайный интервал времени.
Стоимость поставки. Как правило, предполагается, что стоимость каждой поставки слагается их двух компонент - разовых затрат, не зависящих от объема заказываемой партии, и затрат, зависящих (чаще всего линейно) от объема партии.
Издержки хранения. В большинстве моделей управления запасами считают объем слада практически неограниченным, а в качестве контролирующей величины служит объем хранимых запасов. При этом полагают, что хранение каждой единицы запаса в единицу времени взимается определенная плата.
Штраф за дефицит. Любой склад создается для того, чтобы предотвратить дефицит определенного типа изделий в обслуживаемой системе. Отсутствие запаса в нужный момент приводит к убыткам, связанным с простоем оборудования, неритмичностью производства и т.п. Эти убытки называют штрафом за дефицит.
Номенклатура запаса. В простейших случаях предполагается, что на складе храниться запас однотипных изделий или однородного продукта. В более сложных случаях рассматривается многономенклатурный запас.
Структура складской системы. Наиболее полно разработаны математические модели одиночного слада. Однако на практике встречаются и более сложные структуры: иерархические системы сладов с различными периодами пополнения и временем доставки заказов, с возможностью обмена запасами между складами одного уровня иерархии и т.п.
В качестве критерия эффективности принятой стратегии управления запасами выступает функция затрат (издержек), представляющая суммарные затраты на поставку запасаемого продукта, его хранение и затраты на штрафы.
Управление запасами состоит в отыскании такой стратегии пополнения и расхода запасами, при котором функция затрат принимает минимальное значение.
Пусть фукнции  ,
,  и
и  выражают соответственно:
выражают соответственно:
 - пополнение запасов,
- пополнение запасов,
 - расход запасов,
- расход запасов,
 - спрос на запасаемый продукт
- спрос на запасаемый продукт
за промежуток времени  .
.
В моделях управления запасами обычно используются производные этих функций по времени  ,
,  ,
,  ,называемые соответственно,
,называемые соответственно,
 - интенсивностью пополнения,
- интенсивностью пополнения,
 - интенсивностью расхода,
- интенсивностью расхода,
 - интенсивностью спроса.
- интенсивностью спроса.
Если функции  ,
,  ,
,  - не случайные величины, то модель управления запасами считается детерминированной, если хотя бы одна из них носит случайный характер - стохастической. Если все параметры модели не меняются во времени, она называется статической, в противном случае - динамической. Статические модели используются, когда принимается разовое решение об уровне запасов на определенный период, а динамические - в случае принятия последовательных решений об уровнях запаса или корректировке ранее принятых решений с учетом происходящих изменений.
- не случайные величины, то модель управления запасами считается детерминированной, если хотя бы одна из них носит случайный характер - стохастической. Если все параметры модели не меняются во времени, она называется статической, в противном случае - динамической. Статические модели используются, когда принимается разовое решение об уровне запасов на определенный период, а динамические - в случае принятия последовательных решений об уровнях запаса или корректировке ранее принятых решений с учетом происходящих изменений.
Уровень запаса в момент  определяется основным уравнением запасов
определяется основным уравнением запасов
 , (1)
, (1)
где  - начальный запас в момент
- начальный запас в момент  .
.
Уравнение запасов чаще всего используется в интегральной форме:
 (2)
(2)
Пример 1. Интенсивность поступления деталей на склад готовой продукции составляет в начале дневной смены 3 детали в мин, в течение первого часа интенсивность линейно возрастает, достигая к концу его 6 деталей в мин, и затем остается постоянной. Полагая, что поступление деталей на склад происходит непрерывно в течение восьми часов смены, а вывоз автомашин со склада производится только в конце работы, нужно записать выражение для уровня запаса в произвольный момент времени и, используя его, найти количество деталей на складе:
а) через 40 мин после начала работы; б) в конце смены.
Решение. Так как в течение смены не происходит выдачи деталей со склада, то b (t) = 0. Интенсивность пополнения запаса в течение первого часа линейно возрастает, т.е. a(t) = kt+ m. Учитывая, что a(0) = 3, получаем m = 3. В конце часа (t=60): а(60) = 6, следовательно, 6 = 60k+3, откуда k=0,05. Таким образом, для первого часа смены a(t) = 0,05t+3 , а затем a{t) = 6.
Учитывая продолжительность смены (8 ч = 480 мин) и соотношение (2), получаем, если
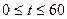



Количество деталей на складе через 40 минут после начала работы будет:
 , а в конце смены
, а в конце смены 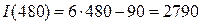
Дата добавления: 2015-01-19; просмотров: 277; Мы поможем в написании вашей работы!; Нарушение авторских прав |