Степенные ряды. Теорема Абеля.

Ответ:Функциональные ряды вида: , где c_n (n=1,2,…) и a–заданные комплексные числа, -комплексное переменное, называют степенными рядами, а числа c_n -коэффициентами степенного ряда (1). Полагая в (1) z= -a, получим ряд (2), исследование сходимости которого эквивалентно исследованию сходимости ряда (1). Теорема 1 (Абеля) . Если степенной ряд (2) сходится при z= 0 , то он сходится, и притом абсолютно, при любом z таком, что |z|<|z₀|; а если этот ряд расходится при z=z₁ 0, то он расходится при всяком z, для которого |z|>|z₁|. а)Пусть k₀ ={z: | z|<|z₀|}- круг на комплексной плоскости с центром в точке О радиуса |z₀|, и пусть z – произвольная точка круга k₀, т.е. |z|<|z₀| , поэтому q=|z/z₀|<1. (3) Так как ряд (2) сходится в точке z₀, то должно выполняться условие , откуда следует ограниченность последовательности { },т.е. M. Используя неравенство (3) и (4), получаем| 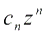|=| |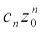*| z/ M , где (5). Так как ряд , где , сходится, то по признаку сравнения сходится ряд ,т.е. ряд (2) сходится абсолютно в каждой точке круга k₀. б)Пусть ряд (2) расходится в точке . Тогда он должен расходиться в любой точке такой, что |z₁|<| |, так как в противном случае по доказанному выше ряд (2) сходился бы в точке z₁. Теорема 2. Для всякого степенного ряда (2) существует R( -число или такое, что: а)если и 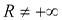, то ряд (2) абсолютно сходится в круге К={z: |z|<R}и расходится вне круга K; этот круг называют кругом сходимости ряда (2), а R-радиусом сходимости ряда; б)если R=0, то ряд (2) сходится в одной точке z=0; в)если , то этот ряд сходится во всей комплексной плоскости. Теорема 3 (Абеля). Если R-радиус сходимости степенного ряда (2), причем , и если этот ряд сходится z=R, то он сходится равномерно на отрезке [0,R], а его сумма непрерывна на этом отрезке. Теорема 4. Если существует конечный или бесконечный , то для радиуса R сходимости ряда (2) справедлива формула 1/R= , а если существует конечный и бесконечный 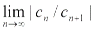, то R= 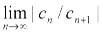. 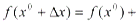0, .