
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Функция комплексного переменного.
Ответ:Основные понятия, связанные с функцией комплексного переменного, находятся так же, как и в действительной области. Пусть заданы два множества  и
и 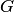 комплексных чисел.
комплексных чисел.
Если каждому значению 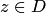 ставится в соответствие число
ставится в соответствие число 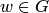 , то говорят, что на множестве
, то говорят, что на множестве  задана функция
задана функция  комплексного переменного, т.е. Если записать числа
комплексного переменного, т.е. Если записать числа  и
и 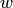 в алгебраической форме:
в алгебраической форме: 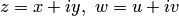 , то замечаем, что действительная
, то замечаем, что действительная 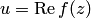 и мнимая
и мнимая  части функции
части функции 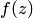 являются функциями переменных
являются функциями переменных 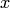 и
и  и
и 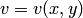 . Задание функции
. Задание функции 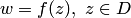 эквивалентно заданию на множестве
эквивалентно заданию на множестве  двух функций
двух функций  двух действительных переменных. Кроме того, если для числа
двух действительных переменных. Кроме того, если для числа 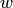 записать модуль
записать модуль 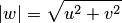 и аргумент
и аргумент  для
для  и
и 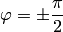 при
при 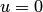 (
(  при
при  и
и 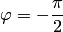 при
при 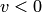 ), то получим аналогичное утверждение. Задание функции комплексного переменного
), то получим аналогичное утверждение. Задание функции комплексного переменного  равносильно заданию двух функций двух действительных переменных. Первая из функций определяет модуль функции:
равносильно заданию двух функций двух действительных переменных. Первая из функций определяет модуль функции: 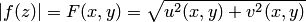 , вторая — аргумент функции:
, вторая — аргумент функции: 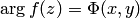 , где
, где 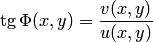 в точках, в которых
в точках, в которых 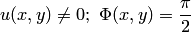 при
при 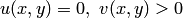 и
и 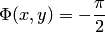 при
при 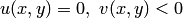 .
.
Дата добавления: 2015-01-19; просмотров: 133; Мы поможем в написании вашей работы!; Нарушение авторских прав |