
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные размеры шестерни и колеса
Делительные диаметры:
шестерни
 , (2.21)
, (2.21)
где mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)];
cos β = 0,975 – косинус угла наклона зубьев [см. формулу (2.20)];
Z1 = 26 – число зубьев шестерни [см. формулу (2.18)], тогда
 ;
;
колеса
 , (2.22)
, (2.22)
где mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)];
cos β = 0,975 – косинус угла наклона зубьев [см. формулу (2.20)];
Z2 = 130 – число зубьев колеса [см. формулу (2.19)], тогда
 .
.
Проверка:аw = (d1+d2)/2 = ( 66,67 + 333,33 )/2 = 200 мм.
Диаметры окружностей вершин зубьев:
 шестерни da1 = d1+2· mn , (2.23)
шестерни da1 = d1+2· mn , (2.23)
где d1 = 66,67 мм – делительный диаметр шестерни [см. формулу (2.21)];
mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)], тогда
da1 = 66,7 + 2 · 2,5 = 71,67 мм;
колеса
da2 = d2+2· mn, (2.24)
где d2 = 333,33 мм – делительный диаметр колеса [см. формулу (2.22)];
mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)], тогда
da2 = 333,33 +2 · 2,5 = 338,33 мм.
Диаметры окружностей впадин зубьев: шестерни
db1 = d1– 2,5· mn, (2.25)
где d1 = 66,67 мм – делительный диаметр шестерни [см. формулу (2.21)];
mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)],
тогда db1 = 66,67 –2,5 · 2,5 ≈ 60,42 мм;
колеса
db2 = d2 – 2,5· mn, (2.26)
где d2 = 333,33 мм – делительный диаметр колеса [см. формулу (2.22)];
mn = 2,5 мм – нормальный модуль зацепления [см. формулу (2.17)], тогда
db2 = 333,33 – 2,5· 2,5 = 327,08 мм.
Ширина зубчатого венца колеса
b2 = ψbα·αw, (2.27)
где  = 0,4 – коэффициент ширины венца для косозубых колес (см. выше);
= 0,4 – коэффициент ширины венца для косозубых колес (см. выше);
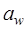 = 200 мм – межосевое расстояние [см. формулу (2.16)], тогда
= 200 мм – межосевое расстояние [см. формулу (2.16)], тогда
b2 = 0,4·200 = 80 мм.
Ширина венца шестерни.
Для того, чтобы длина линии контакта зубьев не уменьшалась при возможном осевом смещении колес, обычно шестерня делается немного шире колеса, в данном случае на 5 мм:
b1 = b2+5, (2.28)
где b2 = 80 мм – ширина венца колеса [см. формулу (2.27)], тогда
b1 = 80+5 = 85 мм.
 Коэффициент ширины шестерни по диаметру
Коэффициент ширины шестерни по диаметру
ψbd1 = b1/ d1, (2.29)
где b1 = 85 мм – ширина венца шестерни [см. формулу (2.28)];
d1 = 66,67 мм – делительный диаметр шестерни [см. формулу (2.21)],
тогда ψbd = 85 / 66,67 = 1,275 .
Произошло увеличение этого коэффициента из-за увеличения ширины шестерни по формуле (2.28).
Окружная скорость колеса и степень точности передачи
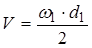 , (2.30)
, (2.30)
где ω1 = ωдв = 101,9 рад/с – угловая скорость вала электродвигателя [см. формулу (2.7)];
d1 = 66,67 мм – делительный диаметр шестерни [см. формулу (2.21)],
тогда 
Для косозубых колес при скорости до 10 м/с назначают 8-ю степень точности.
Таблица 2.7
Значение коэффициента КHβ

| Расположение колес передачи относительно опор | |
| нес мм тр чное | симметричное | |
| 1,2 - ψвd1 | 1,5 КНВ1 | |
| 1,25 - ψвd | Расчёт КНВ | |
| 1,4 - ψвd2 | 1,18 КНВ2 |
Коэффициент нагрузки
КН = КНβ·КНα·КHV. (2.31)
Значение КНβ выбираем по табл. 2.7. Значение ψbd = 1,275 не совпадает с табличными значениями, поэтому для отыскания соответствующего ему значения КНβ применили формулу линейной интерполяции:
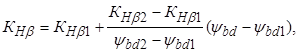
где ψbd1 = 1,2; ψbd2 = 1,4; КНβ1 = 1,15; КНβ2 = 1,18 (для несимметричного расположения колес с учетом изгиба ведомого вала от натяжения цепной передачи):
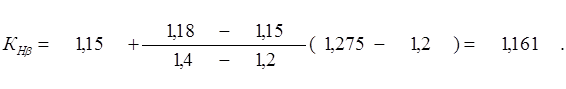
 Значения КНа даны в табл. 2.8.
Значения КНа даны в табл. 2.8.
Таблица 2.8
| Значение КНа для косозубых и шевронных передач | ||||
| Степень точности | Окружная скорость V, м/с | |||
| V1 До 1 | 3,4 V | V2 5 | ||
| КНα1 1,06 | 1,072 | КНα2 1,09 |
Таким же образом по формуле линейной интерполяции

находим при V = 3,4 м/с, степени точности 8 коэффициент
 .
.
Значения КHV приведены в табл. 2.9.
Таблица 2.9
| Передача | Окружная скорость V, м/с | |||
| (3,4) до 5 | ||||
| Степень точности | ||||
| Косозубая | 1,0 |
При V = 3,4 м/с, степени точности 8 для косозубых колес имеем КHV = 1,0.
Таким образом, КН = 1,161 · 1,072 ·1 = 1,245
Проверка контактного напряжения:
 , (2.32)
, (2.32)
где Т2 = 605·103 Н·мм – вращающий момент на валу колеса [см. формулу (2.11)];
КН = 1,245 – коэффициент нагрузки [см. формулу (2.31)];
u = uред = 5 – передаточное отношение редуктора (см. выше);
b2 = 80 мм – ширина колеса [см. формулу (2.27)];
 [σН] =409 МПа – допускаемое контактное напряжение для косозубых колес [см. формулу (2.15)], тогда
[σН] =409 МПа – допускаемое контактное напряжение для косозубых колес [см. формулу (2.15)], тогда

σН ≤ [σН],
385 МПа ≤ 409 МПа. Условие выполнено.
Дата добавления: 2014-10-31; просмотров: 409; Мы поможем в написании вашей работы!; Нарушение авторских прав |