Оценка результатов измерений как случайных величин

Оценка результатов нескольких серий измерений

Цель работы

- получение практических навыков выполнения измерений;

- ознакомление с вероятностным подходом к оценке результатов измерений;

- получение навыков обработки результатов нескольких серий измерений.

Теоретические положения

Оценка результатов измерений как случайных величин

При проведении с одинаковой тщательностью и в одинаковых условиях повторных измерений одной и той же неизменяющейся величины мы получаем результаты, некоторые из которых отличаются друг от друга, а некоторые совпадают. Такие результаты говорят о наличии в них случайных погрешностей, то есть погрешностей, изменяющихся хаотически, непредсказуемо.

Рассмотрение случайных погрешностей (и, соответственно, результатов однократных измерений) как случайных событий дает основание использовать математический аппарат теории вероятностей и математической статистики для оценки случайных погрешностей и нахождения значения измеряемой величины, более близкого к истинному значению, чем результат одного измерения.

Теория вероятностей называет случайным такое событие, которое может произойти или не произойти. Применительно к измерениям можно сказать, что при повторных измерениях в одинаковых условиях каждая из множества возможных незначительных причин случайных изменений результатов может или появиться, или не появиться. Количественная оценка объективной возможности появления события называется его вероятностью. Вероятность достоверного события равна 1, а вероятность невозможного события - 0. Эти события неслучайные; для случайных событий вероятности их появления больше нуля и меньше единицы.

Наиболее универсальным способом описания случайных величин (в том числе результатов измерений и случайных погрешностей) являются законы распределения вероятности. Законом распределения вероятности случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Если на процесс измерения действуют несколько влияющих факторов, а вклад каждого из факторов незначителен по сравнению с их суммарным воздействием, то, согласно центральной предельной теореме теории вероятностей, результат измерения физической величины X подчиняетсянормальному закону или закону Гаусса.

На рис. 1 показаны кривые плотности вероятности или дифференциальной функции нормального распределения. Аналитически эта функция описывается выражением

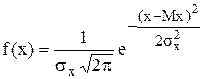, (1)

где Мх - математическое ожидание случайной величины Х,

σ_x - среднее квадратическое отклонение (СКО) случайной величины.

Рис.1. Кривые функций нормального распределения.

Математическим ожиданием(Мх) случайной величины Х называется такое её значение, вокруг которого группируются результаты отдельных наблюдений; при нормальном распределении математическому ожиданию соответствует наибольшая плотность вероятности.

Статистической оценкой математического ожидания для ряда однородных результатов является среднее арифметическое:

. (2)

Среднее квадратическое отклонение (СКО)s_x случайной величины представляет собой меру рассеивания значений случайной величины относительно её математического ожидания

,

где D_x - дисперсия случайной величины:

Чем больше дисперсия (или среднее квадратическое отклонение), тем значительнее рассеивание. Например, Dx₂ > Dx₁ (рис.1).

Статистической оценкой СКО является так называемое стандартное отклонение:

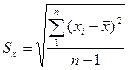, (3)

где n - число наблюдений (измерений).

Вероятность попадания случайной величины в интервал (х₁, х₂) равна:

, (4)

что соответствует площади под кривой распределения на этом участке (рис.1).

Интервал e, который с заданной вероятностью Р покрывает истинное значение случайной величины, называется доверительным интервалом, а вероятность Р - доверительной вероятностью. Как правило, доверительный интервал ±ε располагается симметрично по отношению к математическому ожиданию.

Отношение доверительного интервала к среднему квадратическому отклонению - это относительный доверительный интервал:

(5)

При достаточно большом числе наблюдений (измерений) вычисленное стандартное отклонение близко к действительному значению среднего квадратического отклонения. Если при этом установлено, что закон распределения вероятности результатов измерения - нормальный, то для нахождения относительного доверительного интервала по доверительной вероятности (и наоборот, доверительной вероятности по относительному доверительному интервалу) используются математические таблицы специальной функции Лапласа. Аргументом функции Лапласа является относительный доверительный интервал, рассчитываемый по формуле:

(6)

Однако действия с функцией Лапласа оказываются тем менее надежными, чем меньше число наблюдений. В подобных случаях следует определять доверительную вероятность или доверительный интервал по таблицам распределения Стьюдента, в зависимости от доверительной вероятности и числа наблюдений (табл.2 приложения).