Численные методы интерполирования функций. Постановка задачи. Первая формула Ньютона для равноотстоящих узлов

В практических задачах часто возникает необходимость представлять сложную аналитическую функцию более простой, либо использовать функции, заданные таблично. Необходимо для дальнейшего исследования представить табличную функцию в виде аналитической.

Существуют различные способы получения таких функций. Один из них интерполирование. В общем виде, задачи интерполирования формулируются так:

Пусть функция y=f(x) задана в (n+1) точке x₀,x_1­,…,x_n своими значениями y₀,y₁,…,y_n, то есть y₀=f(x₀), …, y_n=f(x_n).

Требуется подобрать достаточно простую функцию , удовлетворяющую следующим условиям:

1) В точке x₀,x_1­,…,x_n, значения функции должны совпадать со значениями данной функции: , k=0,1,…,n.

2) Во всех остальных точках из области определения, выполняется приближенное равенство: .

Функция называется интерполирующей, процесс ее построения - интерполированием, точки x₀,x_1­,…,x_n - узлами интерполирования. Интерполирующая функция подбирается из определенного класса функций. Часто в качестве такой функции берется многочлен n-й степени, процесс построения такого многочлена - параболическое интерполирование.

Пусть для функции y=f(x) заданы значения y_i=f(x_i) для равноотстоящих значений независимой переменной: x_i=x₀+ih, где i=0..n, h=(b-a)/n, h - шаг интерполяции. Требуется подобрать полином P_n(x) сте­пени не выше n, принимающий в точках x_i значения P_n(x_i)=y_i.

Первой интерполяционной формулой Ньютона называют многочлен вида

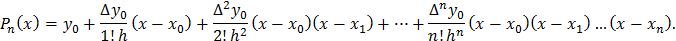
Легко видеть, что этот многочлен полностью удовлетворяет требованиям поставленной задачи. Действительно, во-первых, степень полинома не выше n, во-вторых,

На практике чаще 1-ый интерполяционный многочлен Ньютона используют в другом виде. Обозначим , тогда

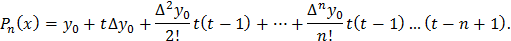
Абсолютную погрешность 1-ой формулы можно оценить следующим образом:

Вторым интерполяционным многочленом Ньютона называется многочлен вида:

На практике удобней пользоваться другой формулой:

Обозначим , тогда =t+1 , = t+2… =t+n-1, тогда многочлен примет вид:

.