Временная сложность алгоритмов.

Временная сложность (ВС) – зависимость времени выполнения алгоритма от количества обрабатываемых входных данных. Здесь представляет интерес среднее и худшее время выполнения алгоритма. ВС можно установить с различной точностью. Наиболее точной оценкой является аналитическое выражение для функции: t=t(N),где t – время, N – количество входных данных (размерность). Данная функция называется функцией временной сложности (ФВС).

Например: t = 5N² + 3*2N + 1. Такая оценка может быть сделана только для конкретной реализации алгоритма и на практике обычно не требуется. Часто бывает достаточно определить лишь порядок функции временной сложности t(N).

Две функции f₁(N)и f₂(N)—одного порядка, если

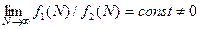
Иначе это записывается в виде: f₁(N)=О(f₂(N)) (Читается " О большое ").

В информатике недостаточно высказать утверждение о существовании некоторого объекта (в математике для этого пользуются теоремами о существовании), а также недостаточно найти конструктивное доказательство этого факта, т.е. алгоритм. В информатике необходимо, чтобы решение задачи можно было осуществить, используя конечный объем памяти и время, приемлемое для пользователя.

По временной сложности все задачи классифицируются следующим образом:
1 класс. Задачи класса Р - это задачи, для которых известен алгоритм и временная сложность оценивается полиномиальной функцией . Алгоритмы таких задач называют также "хорошими" алгоритмами. Этих алгоритмов мало, они образуют небольшой по мощности класс. Легко реализуются. Функция временной сложности для таких алгоритмов имеет вид .
2 класс. Задачи класса Е - это задачи, для которых алгоритм известен, но сложность таких алгоритмов , где f - константа. Задачи такого класса - это задачи построения всех подмножеств некоторого множества, задачи построения всех полных подграфов графа. При небольших N экспоненциальный алгоритм может работать быстрее полиномиального.
3 класс. На практике существуют задачи, которые не могут быть отнесены ни к одному из вышерассмотренных классов. Это прежде всего задачи, связанные с решением систем уравнений с целыми переменными, задачи определения цикла, проходящего через все вершины некоторого графа, задачи диагностики и т.д. Такие задачи независимы от компьютера, от языка программирования, но могут решаться человеком.

Примеры определения порядка ВС для некоторых алгоритмов:

1) Алгоритм линейного поиска. Этот алгоритм может быть использован как для упорядоченного, так и для неупорядоченного массива ключей. Работа алгоритма заключается в том, что при просмотре всего массива, начиная с первого и до последнего элемента, ключ из массива сравнивается с искомым ключом. Если результат сравнения положительный – ключ найден. Если же ни одно сравнение не выполнилось с положительным результатом, то ключа в массиве нет.

ФВС для алгоритма линейного поиска: t _{л. п.} = k₁ * N = O(N). Действительно, для отыскания ключа в худшем случае придется просмотреть все элементы массива. При этом время проверки каждого элемента одинаково и не зависит от конкретной вычислительной системы.

Оценим среднее время алгоритма, при этом будем исходить из следующего: пусть P_i – вероятность того, что будет осуществляться поиск элемента с ключом k_i; при этом предположим, что , т.е. ключ со значением k_i не будет отсутствовать (в таблице обязательно есть элемент, поиск которого осуществляется). Среднее время ( ), как следует из алгоритма, пропорционально среднему числу операций сравнения ( ) и равно ~ = . Если ключи имеют одинаковую вероятность P₁=P₂=...P_N=P, а также учитывая, что , N*P=1, P=1/N, тогда ,

т.е. при линейном поиске в среднем необходимо просмотреть половину массива.

Рассмотрим упорядоченную таблицу, у которой элементы упорядочены по частоте обращений (по вероятности). Если имеем такую таблицу, то время – худшее: = О(N).

Распределение осуществляется по закону Зипфа: P_i = c / i, i = 1, 2, … , N, тогда ~ = ,

причем , (N ® ¥)

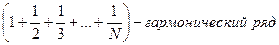, ln N – постоянная Эйлера.

Исходя из этого получили: с = 1 / ln N.

2) Алгоритм бинарного (двоичного) поиска. В словесной форме алгоритм двоичного поиска можно записать следующим образом:

1. Определить середину массива.

2. Если ключ, находящийся в середине массива, совпадает с искомым, поиск завершен.

3. Если ключ из середины массива больше искомого, применить двоичный поиск к первой половине массива.

4. Если ключ из середины массива меньше искомого, двоичный поиск необходимо применить ко второй половине массива.

5. Пункт 1-4 повторять, пока размер области поиска не уменьшается до нуля. Если это произойдет, то ключа в массиве нет.

ФВС для алгоритма бинарного поиска: t _{б. п.} = O(log ₂ N). Это объясняется тем, что на каждом шаге поиска вдвое уменьшается область поиска. До того, как она станет равной одному элементу, произойдет не более log ₂ N таких уменьшений, т.е. выполняется не более log ₂ N шагов алгоритма.

Изобразим графически функции ВС для линейного и двоичного поиска. Из графика видно, что для малых N нужно использовать линейный поиск, а для большихN —двоичный поиск.N_кр находятся в пределах 10 .. 1000 в зависимости от характеристик используемого оборудования.

Задача поиска заключается в том, чтобы определить наличие в массиве элемента, равного заданному. Во многих программах поиск требует наибольших временных затрат, так что замена плохого поиска на хороший, часто ведет к существенному увеличению скорости работы программы. Выбор алгоритма поиска зависит от характера организованности массива.